
- •С. Колеснік
- •Збірник контрольних робіт. Аналітична геометрія та лінійна
- •Контрольна робота № 1
- •Зразки розв’язання задач контрольної роботи №1
- •Розв’язання
- •Контрольна робота № 2
- •Зразки розв’язання задач контрольної роботи №2
- •Контрольна робота № 3
- •1. Перевірити чи утворюють наступні множини векторні простори над полем дійсних чисел r
- •Зразки розв’язання задач контрольної роботи № 3
- •Розв’язання.Нехай м- множина всіх квадратних матриць порядку n з дійсними елементами. Покажемо, що м-абелева група відносно операції додавання.
- •Контрольна робота № 4
- •Зразки розв’язання задач контрольної роботи № 4 і. Для квадратичної форми fзнайти:
- •Контрольна робота №5.
- •Зразки розв’язання задач контрольної роботи №5
- •Контрольна робота № 6
- •Зразки розв’язання задач контрольної роботи № 6
- •Контрольна робота №7
- •Зразки розв’язання задач контрольної роботи № 7
- •Контрольна робота № 8.
- •Зразки роз`язання задач контрольної роботи № 8
- •Для простого модуля старший коефіцієнт взаємнопростий з ним. Визначимо множник k так, щоб . Матимемо . Домножаючи обидві частини заданої конгруенції на 10 за модулем 13, дістаємо
- •Контрольна робота № 9
- •Зразки розв‘язання задач контрольної роботи № 9
- •Тоді з рівності
- •Додаток: таблиці первісних коренів та індексів
- •Література
- •Методичне видання
Контрольна робота № 4
І.
Для квадратичної форми
![]() f
знайти:
f
знайти:
а) матрицю та її ранг;
б) записати форму f у матричному вигляді;
в) методом Лагранжа привести форму f до нормального виду;
г) знайти лінійне перетворення, що приводить форму f до
нормального виду;
д) з’ясувати, чи є форма f позитивно визначеною.
f=x12+5x22+4x32-2x1x2+4x1x3;
f=4x12+4x22+x32-4x1x2+4x1x3-3x2x3;
f=x12-3x32+2x1x2-6x2x3;
f=7x12+6x22+5x32-4x1x2-4x2x3 ;
f=6x12-2x22+6x32+4x1x3;
f=2x12+5x22+x32+2x1x2+2x2x3-16x1x3;
f=x12-2x22+3x32+4x1x2-4x2x3-8x1x3;
f=2x1x2+3x2x3-x1x3;
f=5x1x2-x2x3+x1x3;
f=4x12+5x22+6x32-4x1x2+4x2x3.
II.Запишіть квадратичні форми з матрицею А, якщо
A=
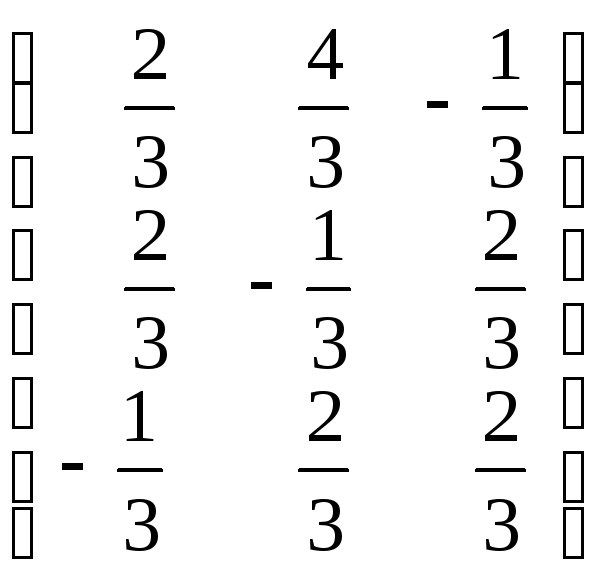 ; 2.
A=
; 2.
A=
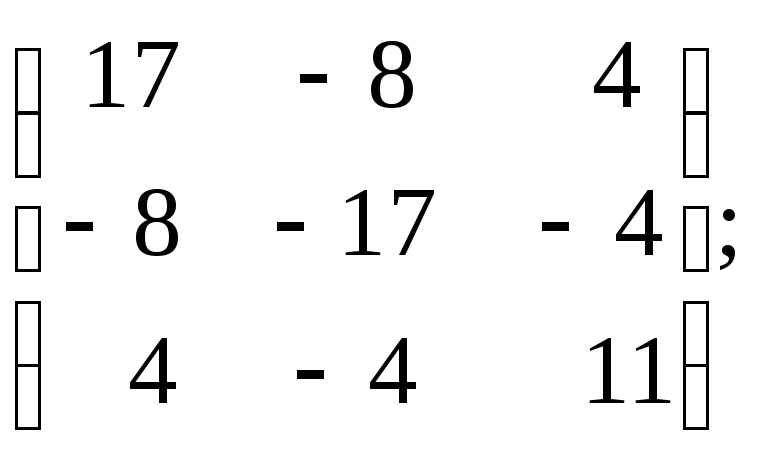 3.
A=
3.
A=

4.
A=
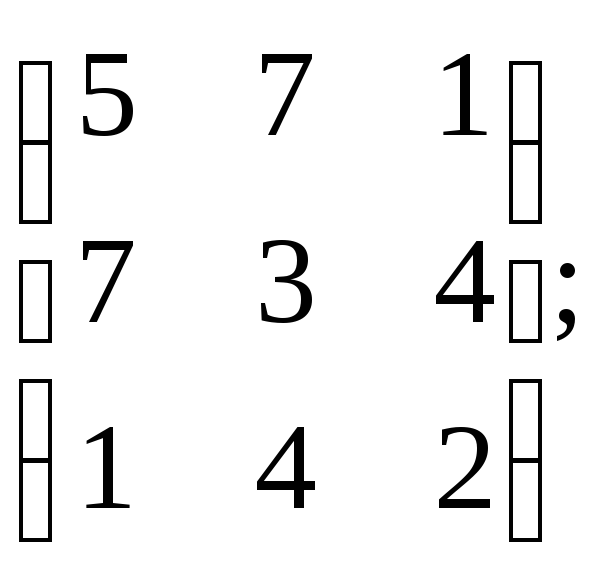
![]() 5.
A=
5.
A=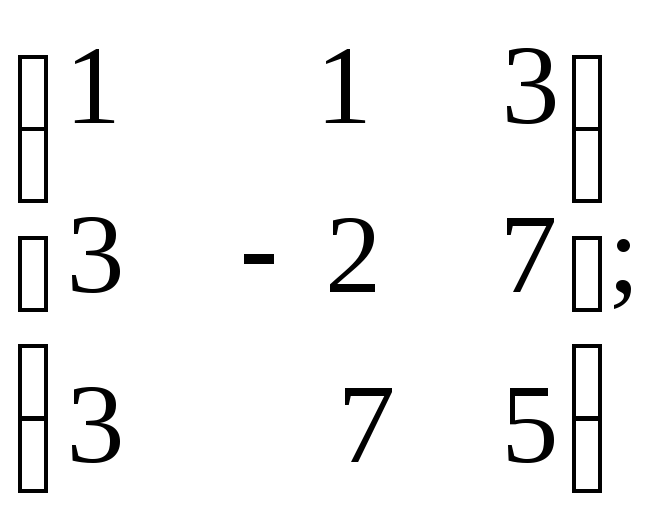 6.
A=
6.
A=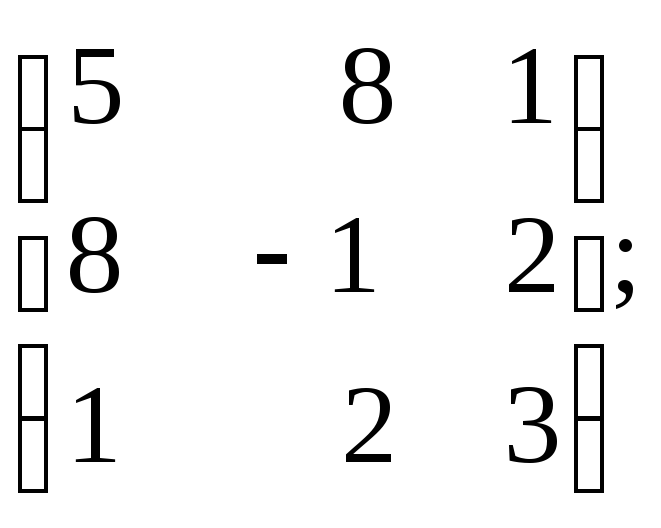
7.
A=
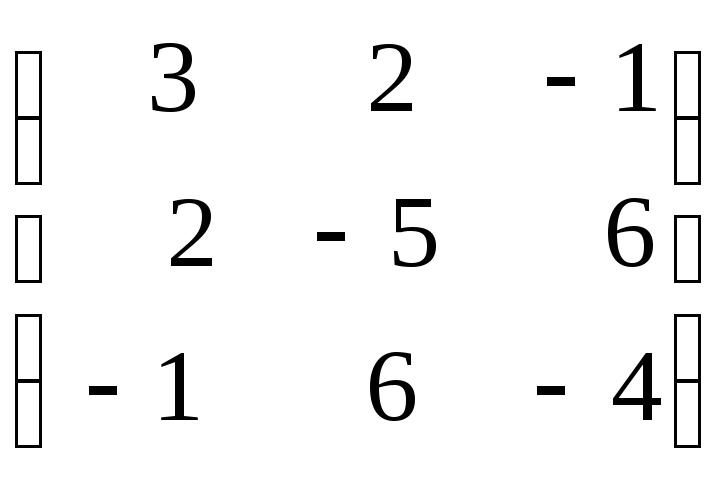 ;
8. A=
;
8. A=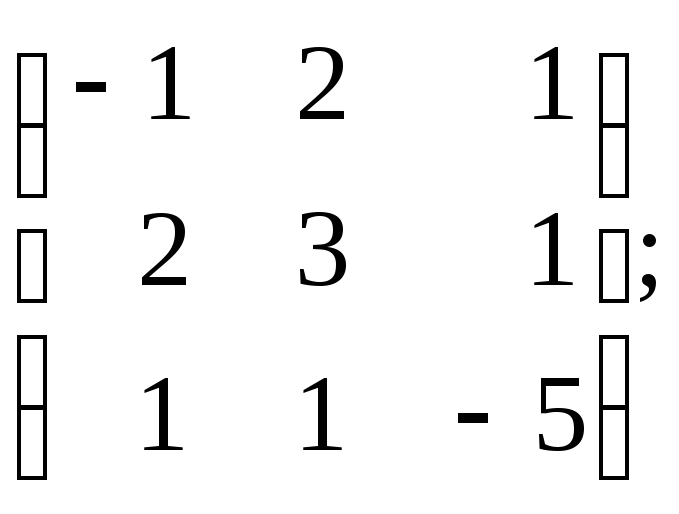 9.
A=
9.
A=
10.
A=
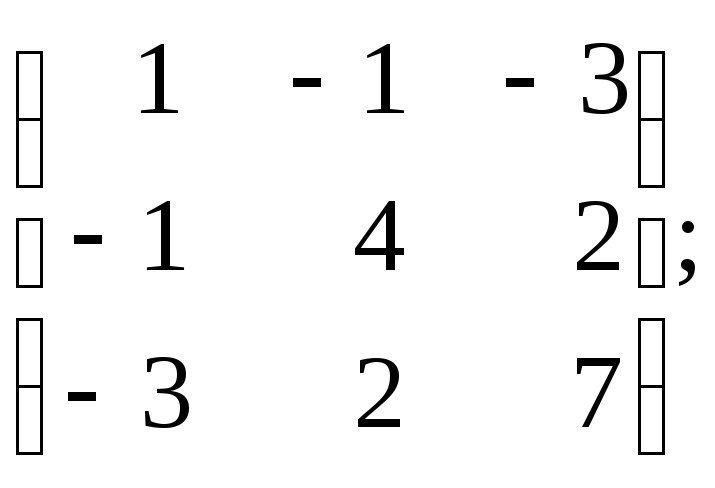
Знайти
ортогональні перетворення, що приводять
квадратичні форми задані в евклідовому
просторі
![]() 3
до канонічного виду. Записати цей
канонічний вид.
3
до канонічного виду. Записати цей
канонічний вид.
f=2x1x2+x22+x12+x3 2 +4x1x3+2x2x3;
f=11x12+5x22+2x32+16x1x2+4x1x3-20x2x3;
f=x12+x22+5x32-6x1x2+6x1x3 –6x2x3;
f=x12+x22+x32+4x1x2+4x1 x3+42x3;
f=17x12+14x22+14x32 –4x1 x2-4x 1x3-8x2 x3;
f=6x12+5x22+7x32-4x1x2+4x1x3 ;
f=4x12+x22+x32-4x1x2+4x 1x3-3x2x3;
f=x12+2x22+3x32-4x1x2-4x2x3;
f=2x12+x22-4x1x2-4x2x3;
f=5x12+7x22+6x32-4x1x3+4x2x3.
IV. Записати канонічне рівняння поверхні другого порядку, визначити її тип та знайти канонічну систему координат.
1. x12+y2+z32+2xy+4xz+2yz-6x+8y-2z-5=0;
2. 11x2+5y2+2z2+16xy+4xz-20yz+4x-6y+8z+1=0;
3. x12+y2+5z2-6xy+6xz-6yz-2x+4y-6z-4=0;
4. x2+y2+z2+4xy+4xz+4yz-6x+4y-2z-1=0;
5. 17x2+14y2+14z2-4xy-4xz-8yz-2x+6y-8z-4=0;
6. 6x2+5y2+7z2-4xy+4xz-8x+2y-2z+3=0;
7. 4x2+y2+z2-4xy+4xz-3yz+4y-6z+2y-4=0;
8. x2+2y2+3z2-4xy-4yz+2y+4z-2x+1=0;
9. 2x2+y2-4xy-4yz+2x-2y+6z-2=0;
10. 5x2+7y2+6z2-4xz+4yz-4x-2y+8z-2=0;
Зразки розв’язання задач контрольної роботи № 4 і. Для квадратичної форми fзнайти:
а) матрицю та її ранг;
б) записати квадратичну форму у матричному вигляді;
в) методом Лагранжа привести форму f до нормального виду;
г) знайти лінійне перетворення, що приводить форму f до
нормального виду;
д) з’ясувати, чи є форма f позитивно визначеною.
Розв’язання:
Нехай f=2x1x2-12x1x3-x22-8x32;
а) Знаходимо матрицю А форми f:
A=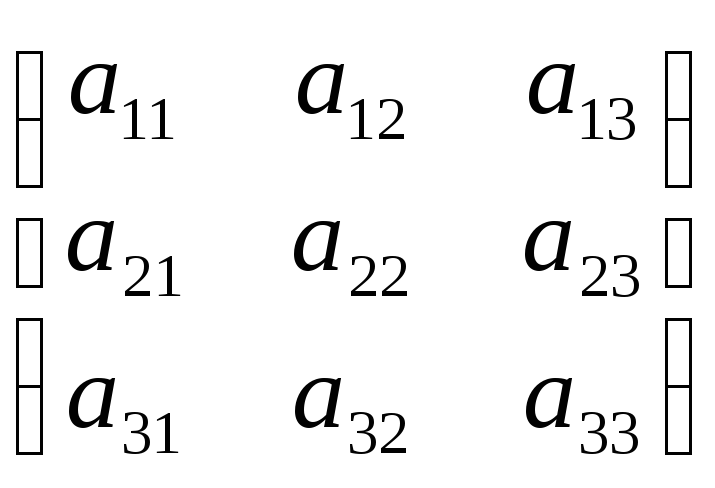 =
=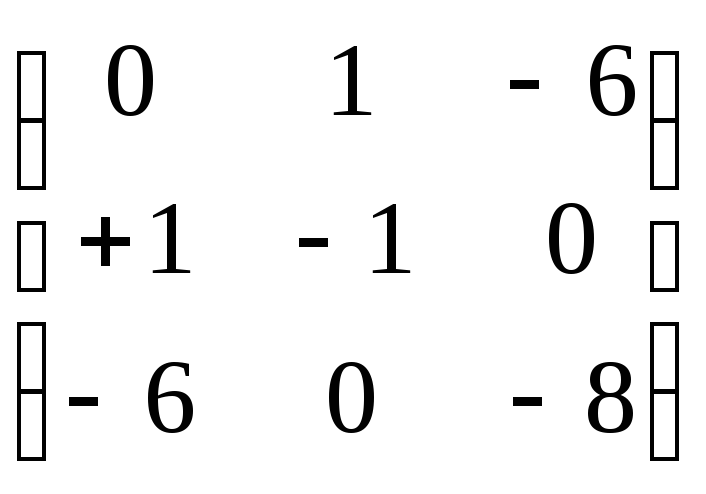
Обчислюємо ранг матриці А.
A= ~
~ ~
~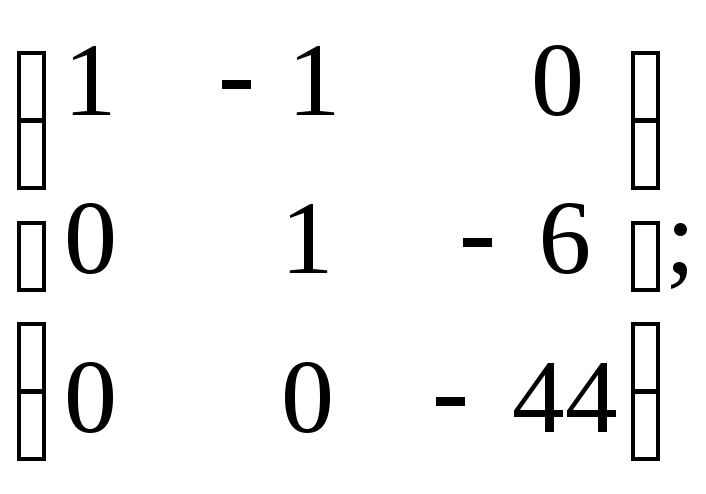 r=3.
r=3.
б) Запишемо квадратичну форму f у матричному вигляді:
Нехай
Х=![]() ,
тодіXT=(х1,х2,х3)
і f=XT·A·X
,
тодіXT=(х1,х2,х3)
і f=XT·A·X
Дійсно,
ХТ·А·Х=(х1,х2,х3)· ·
·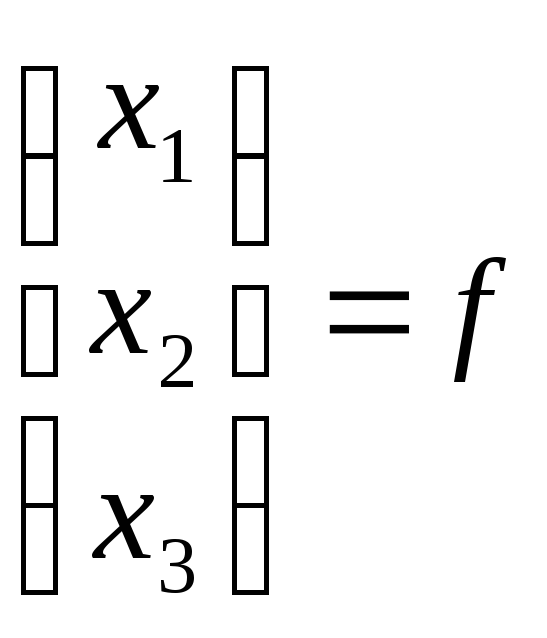 .
.
в) Методом Лагранжа перетворюємо квадратичну форму f до нормального виду.
1-е
перетворення:
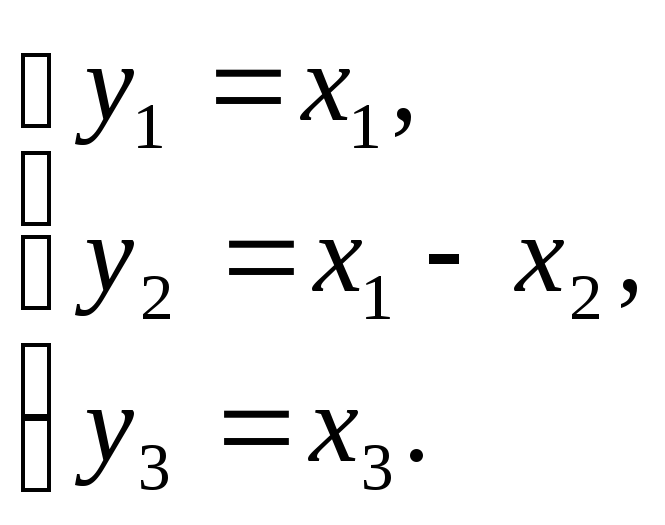
За допомогою 1-го перетворення виділяємо квадрат невідомого х2.
Матриця
цього перетворення Q=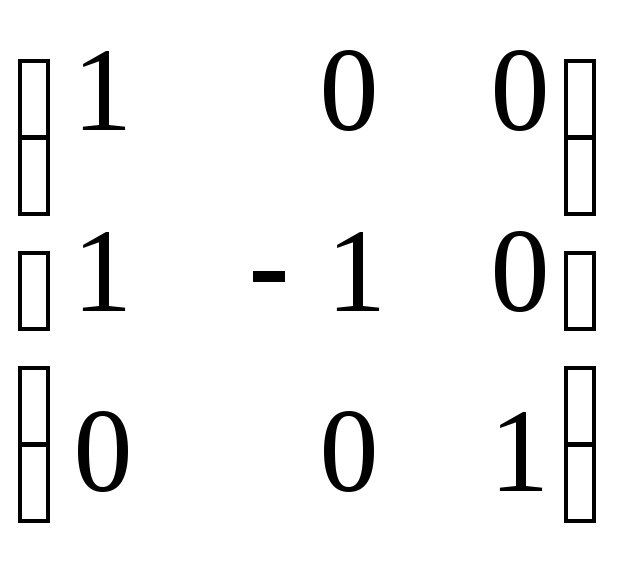 .
.
Знаходимо матрицю, обернену до матриці Q
Q/E=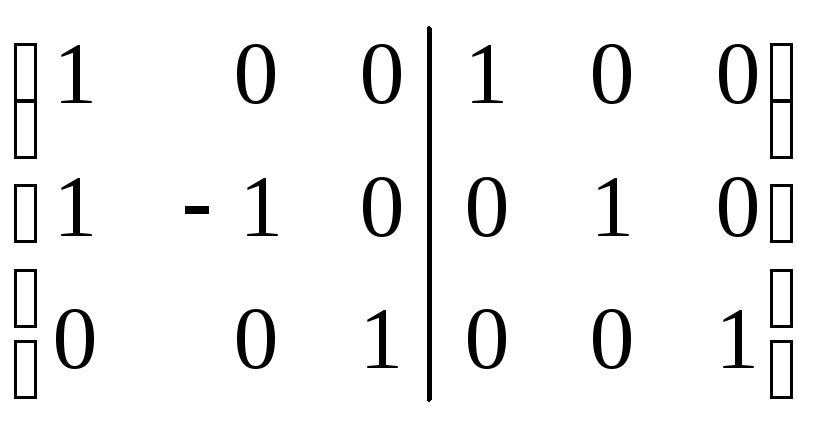 ~
~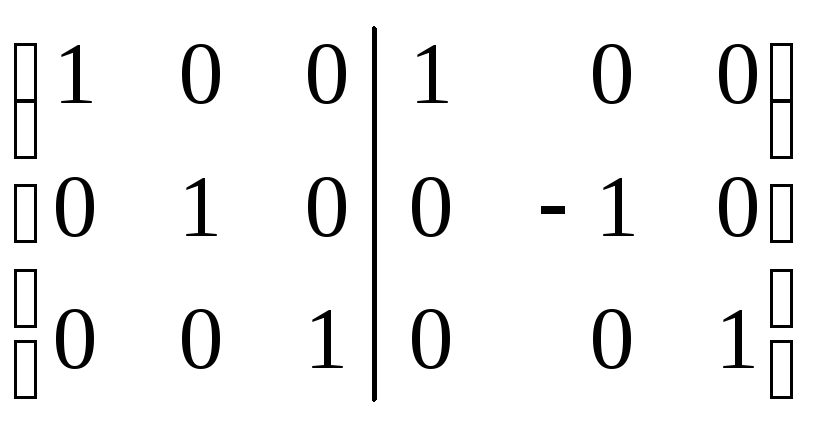
отже,
G-1=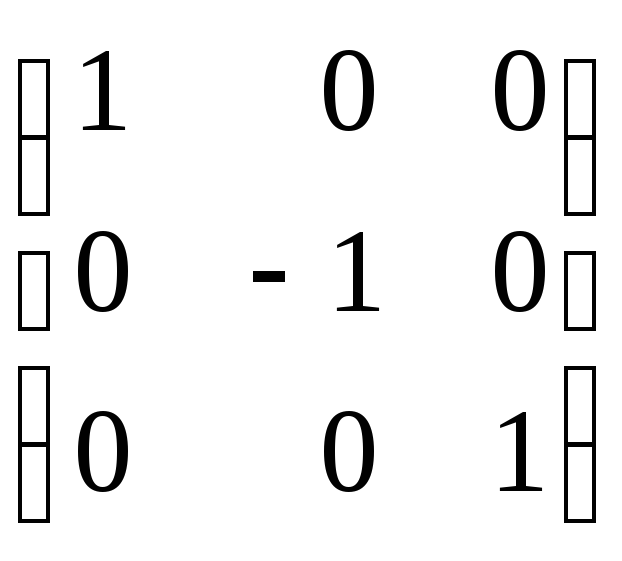 ,
тоді (Q-1)T=
,
тоді (Q-1)T=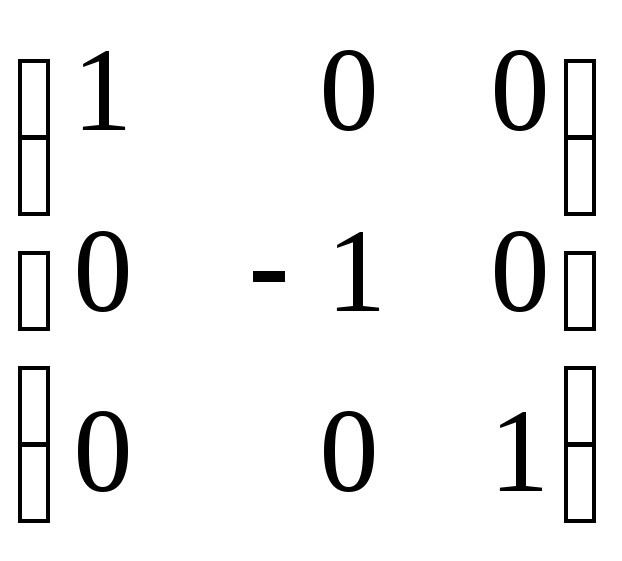
Знаходимо матрицю форми f1, яка одержується з матриці форми f в результаті лінійного перетворення з матрицею Q:
![]() =
=![]() T·Af
·Q-1
T·Af
·Q-1
![]() =
=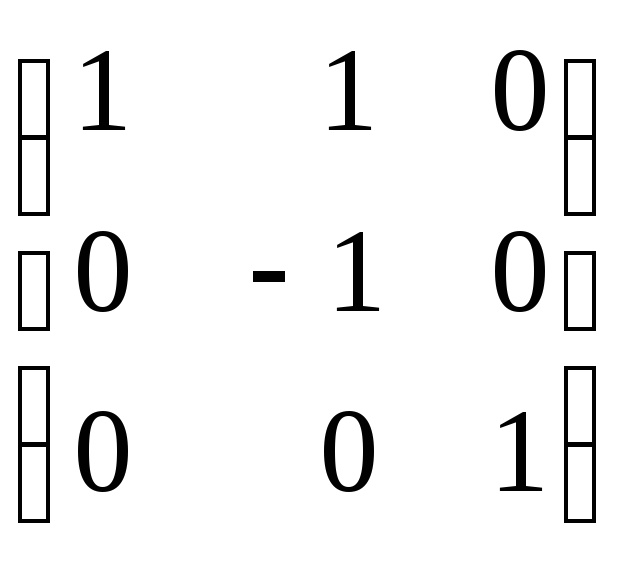 ·
· ·
· =
= .
.
За одержаною матрицею записуємо формулу f1:
f1=y12-y22-8y32-12y1y3.
2- перетворення:
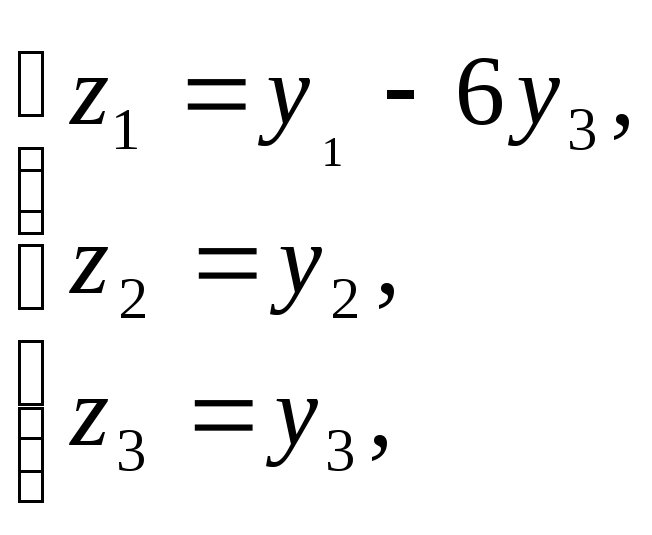 ,
за допомогою якого виділяємо
,
за допомогою якого виділяємо
квадрат
невідомого у1.
Його матриця
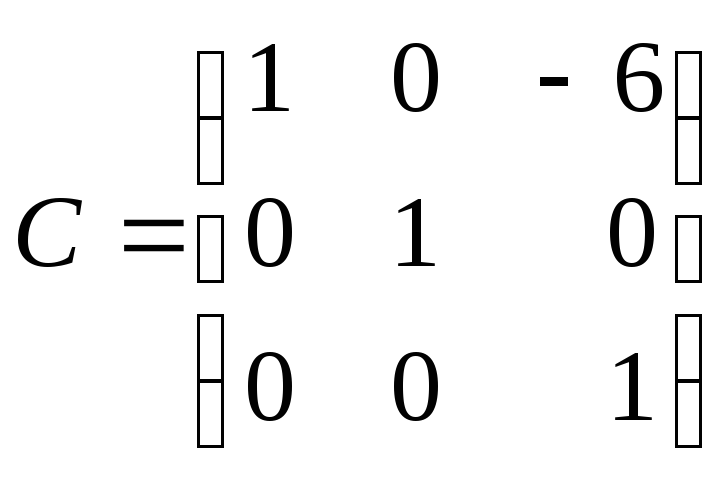 .
.
Знаходимо
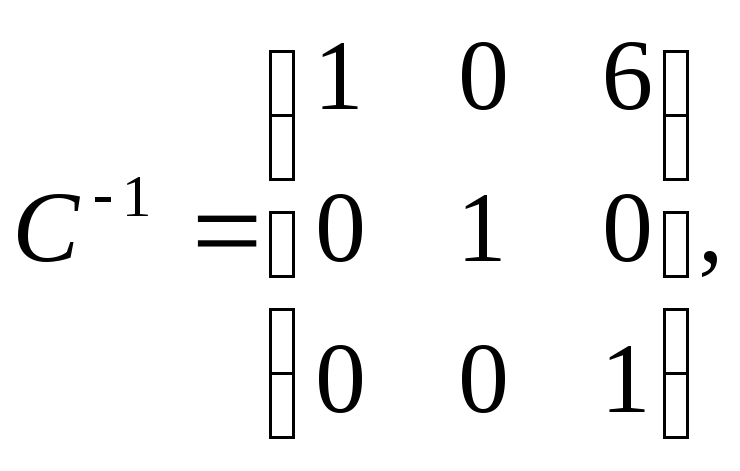 тоді
тоді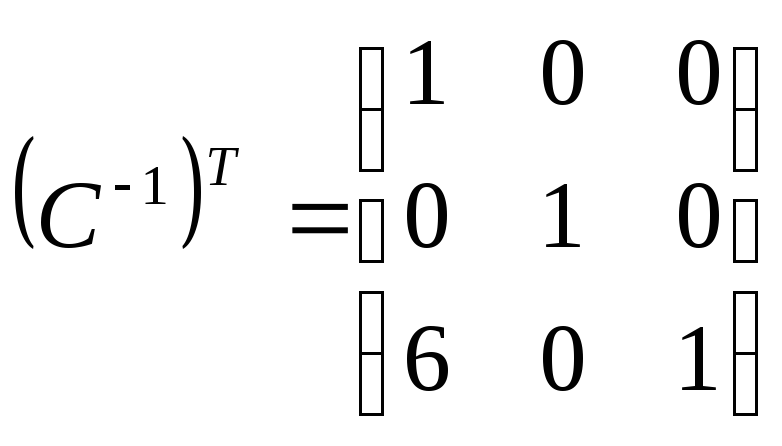 .
.
Обчислюємо
матрицю
![]() ·
·![]() .
.
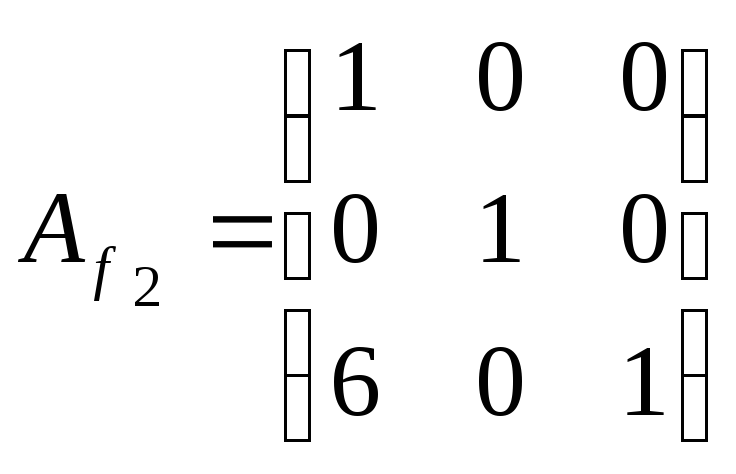 ·
· ·
·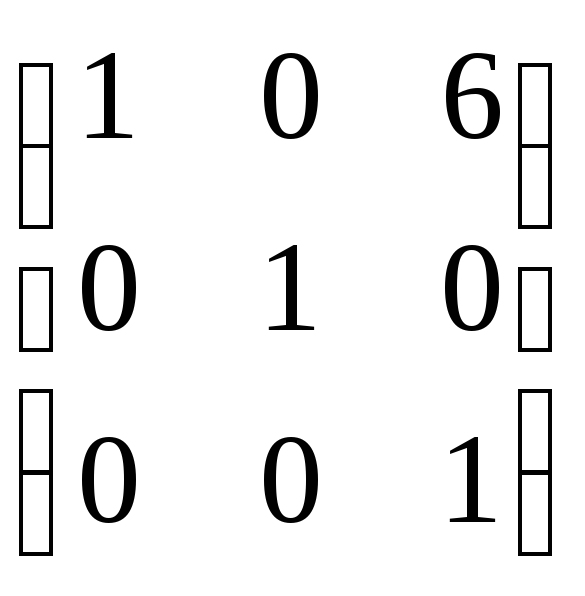 =
= .
.
Матриці
![]() відповідає
квадратична формаf2:
відповідає
квадратична формаf2:
![]() =z12-z22-44z32,
яка має канонічний вид.
=z12-z22-44z32,
яка має канонічний вид.
Зводимо
форму f2
до нормального виду за допомогою
лінійного перетворення:
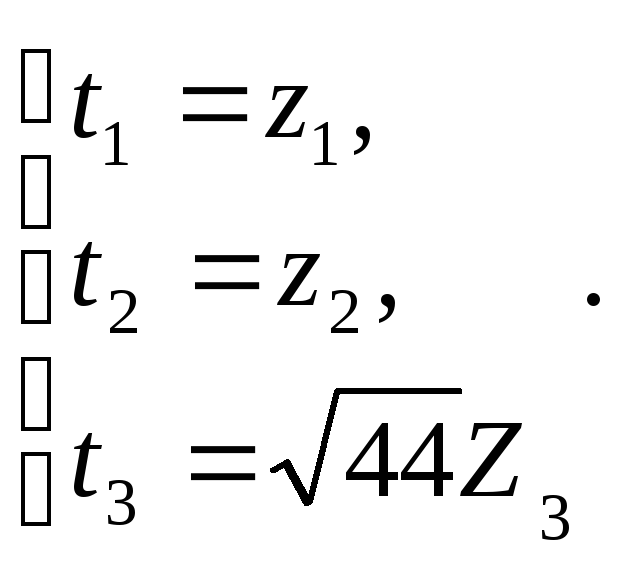 Його
матриця
Його
матриця
 ,
тоді
,
тоді
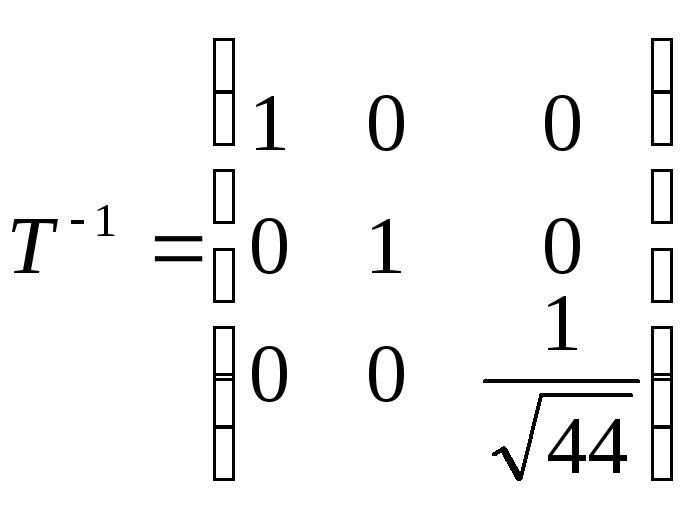 .
.
Тоді
![]()
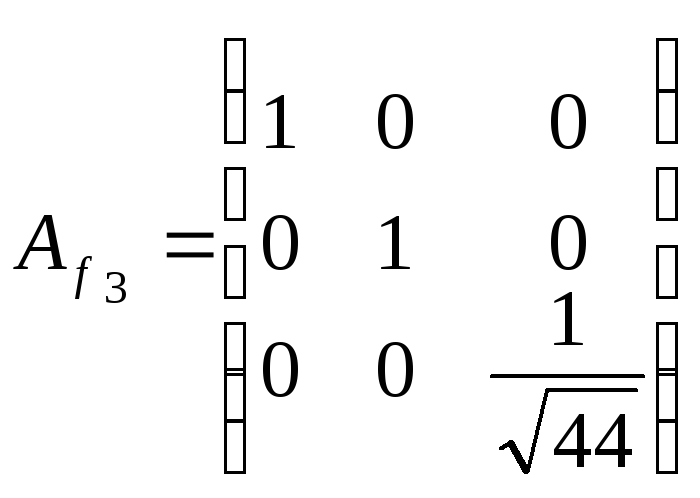 ·
· ·
·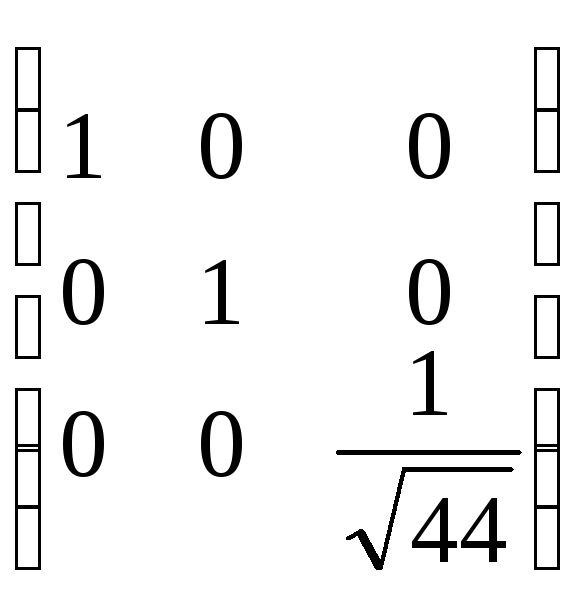 =
= .
.
Отже, f3=t12-t22-t32 – нормальний вид форми f.
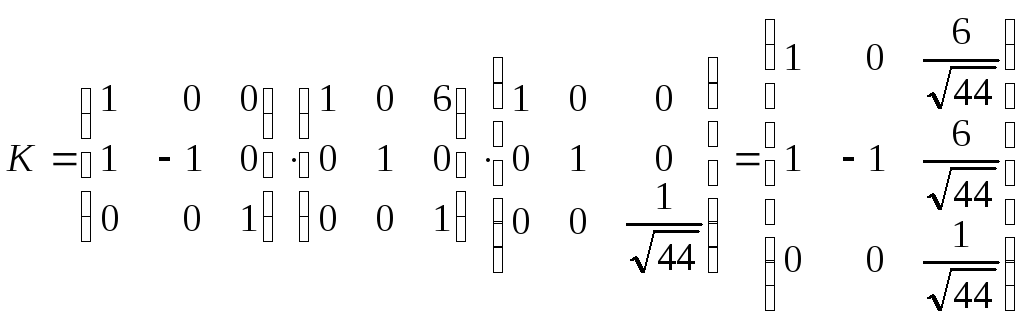 ,
,
тоді
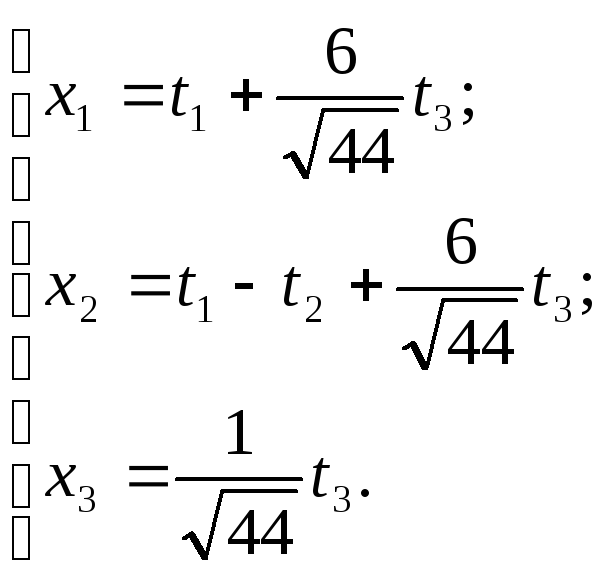
д)
З’ясуємо,
чи є позитивно визначеною квадратична
форма f.
Квадратична
форма f
не буде позитивно визначеною, оскільки
її другий головний мінор
![]() від’ємний.
від’ємний.
II.
Записати
квадратичну форму з матрицею А =
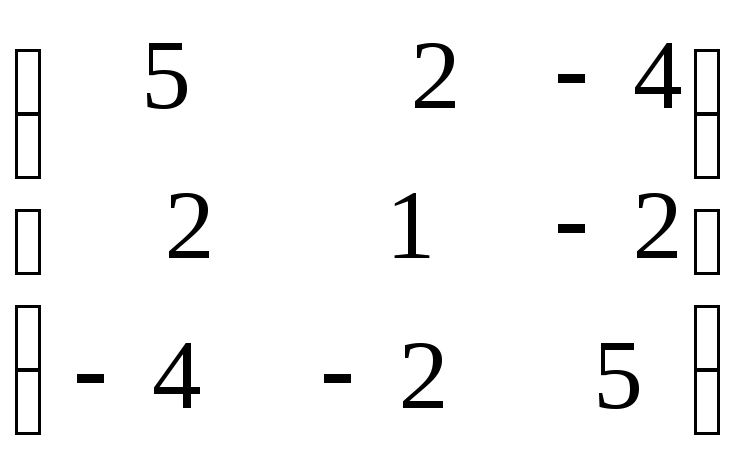
Розв’язання:
Матриці А відповідає наступна квадратична форма f:
f=5x12+x22+5x32+4x1x2-8x1x3-4x2x3.
III. Ортогональним перетворенням невідомих звести до канонічного виду квадратичну форму f=6x12+5x22+7x32-4x1x2+4x1x3.
Розв’язання. Матриця даної квадратичної форми f має вигляд:
А= ,
її характеристична матриця А- λE
=
,
її характеристична матриця А- λE
=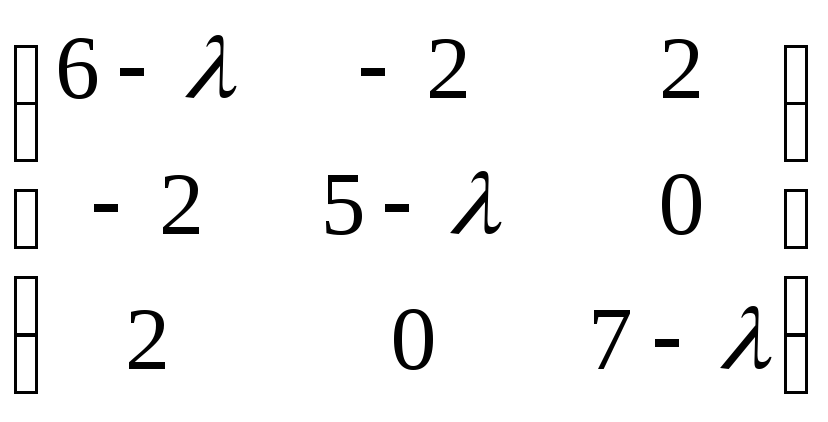 .
.
Розв’яжемо характеристичне рівняння:
|A-
λE
|=0;
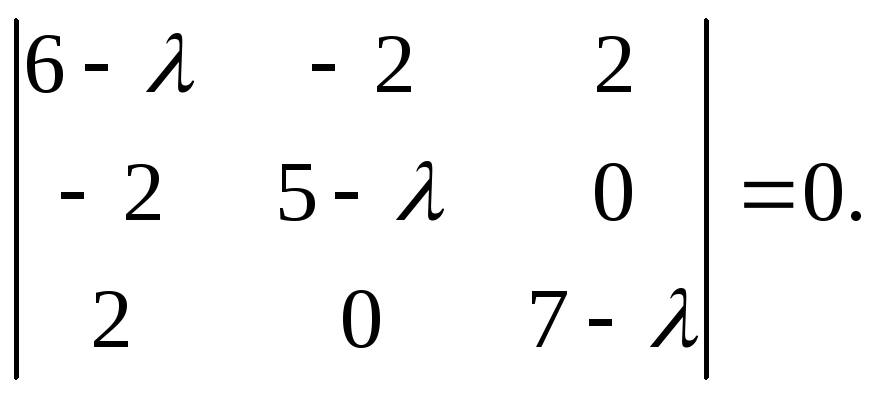
Власні числа цієї матриці λ1=3; λ2=6; λ3=9.
Знаходимо власні вектори, що відповідають цим власним значенням. Для цього розв’яжемо систему лінійних однорідних рівнянь:
(A-λiE)·X=0
Нехай λ1=3. Тоді відповідна система однорідних рівнянь
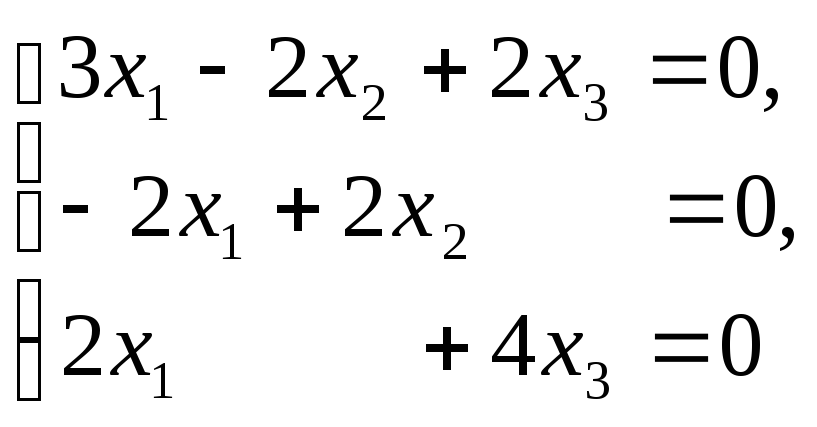
рангу
2 має фундаментальну систему розв’язків,
що складається з одного вектора
![]() який є власним вектором, відповідним
власному значенню λ1=3.
який є власним вектором, відповідним
власному значенню λ1=3.
Нехай λ2=6; одержуємо систему однорідних рівнянь
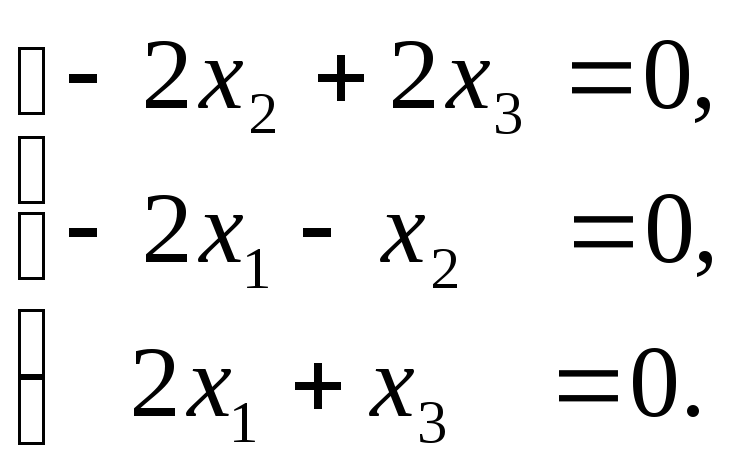
Розв’язавши
її, знаходимо власний вектор
![]() ,
,
Нехай λ3=9. Відповідна система лінійних однорідних рівнянь

має фундаментальну систему розв’язків, що складається з вектора
![]() ,
який і буде власним вектором, відповідним
власному значенню
,
який і буде власним вектором, відповідним
власному значенню
![]() λ3=9.Одержана
система векторів
λ3=9.Одержана
система векторів
![]() ортогональна, отже, лінійно незалежна
і тому є одним з базисів трьохвимірного
векторного простору. Нормуємо її,
відповідні ортонормовані власні вектори
ортогональна, отже, лінійно незалежна
і тому є одним з базисів трьохвимірного
векторного простору. Нормуємо її,
відповідні ортонормовані власні вектори
![]()
![]()
![]() є ортонормованим базисом, в якому задана
квадратична форма має канонічний вид:
є ортонормованим базисом, в якому задана
квадратична форма має канонічний вид:
f1=3y12+6y22+9y32.
Відповідне лінійне перетворення координат має вигляд:
х1=-![]() y1-
y1-![]() y2+
y2+![]() y3;
y3;
х2=-![]() y1+
y1+![]() y2-
y2-![]() y3;
y3;
х3=![]() y1+
y1+![]() y2+
y2+![]() y3.
y3.
IV. Записати канонічне рівняння поверхні другого порядку, визначити її тип та знайти канонічну систему координат:
6х2+5y2+7z2-4xy+4xz-2x+6y-4z-1=0.
Розв’язання. Квадратична частина многочлена лівої частини рівняння має вигляд:
f=6х2+5y2+7z2-4xy+4xz,
її
матриця А= має власні числа
має власні числа![]() =3;
=3;![]() =6;
=6;![]() =9.
=9.
Відповідні ним ортонормовані власні вектори:
![]()
![]()
![]()
Виконаємо ортогональне перетворення невідомих за формулами:
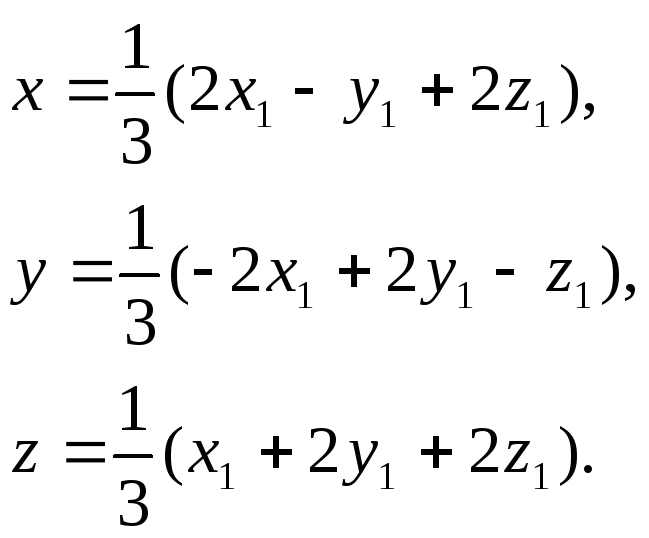
Одержуємо:
![]() .
.
-1=0;
![]() ;
;
Виконаємо перетворення зсуву за невідомими x1, y1, z1.
Друге перетворення координат має вигляд:
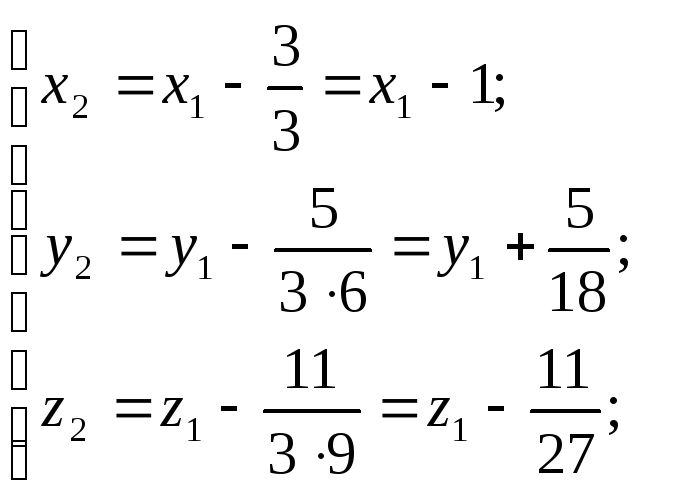
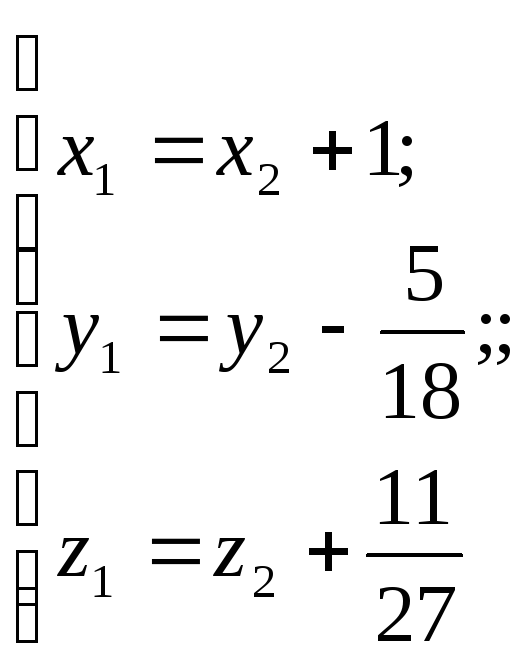
Одержуємо:
![]()
![]() або
або
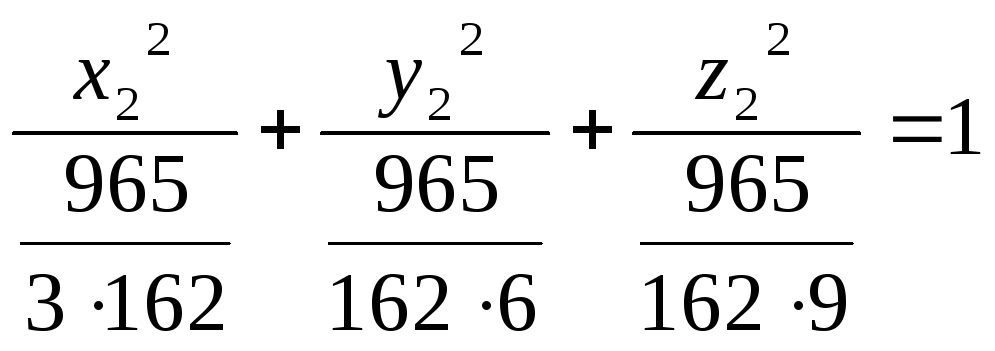 -
канонічне рівняння еліпсоїду.
-
канонічне рівняння еліпсоїду.
Остаточне перетворення координат:

Канонічна система координат:
![]()
![]()
![]()
![]()
