Контрольна робота № 1

Варіант 1.

1. Довести, що із медіан трикутника можна побудувати новий трикутник (застосовуючи апарат векторної алгебри).

2. Знайти точку симетричну з точкою Q(-2,-9), відносно прямої 2x + 5y – 38 = 0.

3. Скласти рівняння прямої, яка проходить через точку перетину прямих 2x + y – 2 = 0 і x – 5y – 23 = 0 та ділить пополам відрізок АВ, де А(5,–6), В( –1,4).

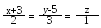
4. З усіх прямих, що перетинають дві прямі: і

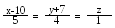
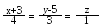
знайти ту, що паралельна прямій

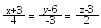
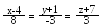
5. Знайти відстань між прямими

6. Через дві точки А(0, 1, -2) і В(2, 1, 0) провести площину перпендикулярну до площини 3x – y + 2z = 0.

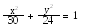
7. Знайти ті дотичні до еліпса , які паралельні прямій 2x – y +17 = 0.

8. Написати рівняння гіперболи з фокусами в точках (3, 0); (-3, 0) та ексцентрисите-том  = 2.

9. Визначити тип поверхні та знайти її найпростіше рівняння:

2x² + 4y² – z² + 8x + 8y – 5 = 0.

10. Зясувати геометричний зміст рівняння та побудувати ескіз x² – 2y² = 4.

Варіант 2.

1. Довести, що середня лінія трикутника дорівнює половині основи і паралельна їй (застосовуючи апарат векторної алгебри).

2. Знайдіть відстань між прямими 3x – 4y + 10 = 0 i 6x – 8y + 15 = 0.

3. Знайти точку, симетричну з точкою М(-2, 5) відносно прямої х – 5у + 7 = 0.

4х + у – 6z – 2 = 0

у – 3z + 2 = 0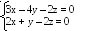

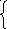
4. Знайти кут між двома прямими: і

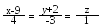
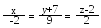
5. Знайти відстань між двома прямими і

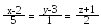
6. Через пряму провести площину перпендикулярну до

площини х + 4у – 3z + 7 = 0.

7. Знайти рівняння тих дотичних до еліпса 3х² + 8у² = 45, відстань яких від центра еліпса дорівнює 3.

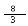
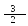8. Скласти рівняння гіперболи, якщо відстань між директрисами

дорівнює і ексцентриситет  = .

9. Визначити тип поверхні та знайти її найпростіше рівняння: x² + y² + 3z² – 6z + 3 = 0.

10.Зясувати геометричний зміст рівняння та побудувати ескіз 2x² + 4y² = 8.

Варіант 3.

1. Довести, що середня лінія трапеції паралельна основам і дорівнює їх півсумі (застосовуючи апарат векторної алгебри).

2. Через точку перетину прямих 2х – 5у – 1 = 0 і х + 4у – 7 = 0 провести пряму, яка ділить відрізок між точками А(4, -3); В(-1, 2) у відношенні  = 2 : 3.

3. Обчислити довжину бісектриси BD кута В трикутника АВС, якщо А(4, 1); В(7, 5); С(-4, 7).

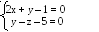
4. З даної точки А(1, 2, -1) провести пряму, що перетинає пряму

під кутом 90^о.

5. Знайти відстань між двома прямими

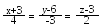
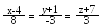
і

6. Скласти рівняння площини, що проходить через початок координат і перпендикулярна до двох площин 2x – y + 5z + 3 = 0 і x + 3y – z – 7 = 0.

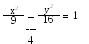
7. До гіперболи провести таку дотичну, яка знаходилась би на однаковій відстані від центра і від правого фокуса.

7. Скласти рівняння еліпса, якщо відстань між директрисами дорівнює 32 і ексцентриситет  = 0,5.

7. Визначити тип поверхні та знайти її найпростіше рівняння:

x² + 5y² + z² – 2х + 20у – 2z – 3 = 0.

7. Зясувати геометричний зміст рівняння та побудувати ескіз 2у² – 6z = 0.

Варіант 4.

1. Довести, що медіани трикутника перетинаються в одній точці. Знайти відношення, в якому точка перетину ділить медіану (застосовуючи апарат векторної алгебри).

2. Відомі рівняння двох суміжних сторін паралелограма х – у – 1 = 0 і х – 2у = 0 та точка перетину його діагоналей М(3, -1). Знайти рівняння двох інших сторін паралелограма.

3. Дано дві точки А(2, 3) і В(1, -1). Провести пряму так, щоб вона пройшла на відстані 3-х одиниць від точки А і на відстані 4 одиниць від точки В.

4. Через точку А(4, 0, -1) провести пряму так, щоб вона перетинала дві дані прямі:

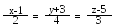
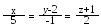
та .

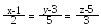
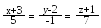
5. Знайти відстань між прямими і .

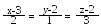
6. Знайти рівняння площини, що проходить через пряму

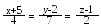
та паралельну прямій .

7. Скласти рівняння дотичної до параболи у² = 28х, перпендикулярної до прямої у – 6х + 1 = 0.

8. Знайти кут між асимптотами гіперболи, у якої відстань між фокусами вдвічі більша відстані між директрисами.

9. Визначити вид поверхні та звести її рівняння до найпростішого вигляду

2x² – 4y² – 5z² + x – 8у + 10z – 8 = 0.

10. Зясувати геометричний зміст рівняння та побудувати ескіз 6x² – 4y² = 0.

Варіант 5.

1. Довести, що сума векторів, що зєднують центр правильного трикутника з його вершинами, дорівнює нулю (застосовуючи апарат векторної алгебри).

2. Скласти рівняння сторін трикутника, знаючи одну з його вершин А(-4, 2) і рівняння двох медіан 3х – 2у + 2 = 0 і 3х + 5у – 12 = 0.

3. На відстані 5 одиниць від початку координат провести пряму так, щоб вона пройшла через ту точку прямої 8х + 5у – 39 = 0, яка має абцису х = 2.

4. З даної точки А(1, 2, -3) опустити перпендикуляр на пряму

5. Знайти відстань між двома прямими

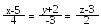
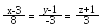
і

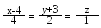6. Знайти рівняння площини, що проходить через точку А(3, 1, -2) і через

пряму .

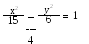
7. До гіперболи провести дотичну паралельну до прямої х + у – 7 = 0.

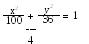
8. На еліпсі знайти точку, відстінь якої від правого фокуса у

чотири рази більша відстані від її лівого фокуса.

9. Визначити тип поверхні та знайти її найпростіше рівняння:

3x² + 4y² – 3z² – 6х + 8у – 9z – 1 = 0.

10. Зясувати геометричний зміст рівняння та побудувати ескіз 3х² – 6у² = 12.

Варіант 6.

1. Довести, що бісектриса внутрішнього кута трикутника ділить протилежну сторону на дві частини, пропорціональні бічним сторонам (застосовуючи апарат векторної алгебри).

2. Відомі рівняння двох суміжних сторін паралелограма: х – у – 1 = 0; х – 2у = 0 та точка перетину його діагоналей М(3, -1). Знайти рівняння двох інших сторін паралелограма.

3. Скласти рівняння сторін трикутника знаючи одну з його вершин А(2, -4) і рівняння бісектрис двох його кутів х + y – 2 = 0 і х – 3у – 6 = 0.

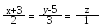
4. Скласти рівняння прямої, яка перетинає прямі та

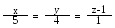
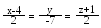
і паралельна прямій .

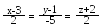
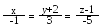
5. Знайти відстань між прямими і .

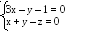
6. Знайти рівняння площини, що проходить через дану пряму

і перпендикулярна до даної площини 7х – у + 2z – 5 = 0.

7. Знайти ті дотичні до гіперболи 4х² – у² = 4, які перпендикулярні до прямої 10у + 3х = 0.

8. Написати рівняння кола, яке проходить через точку (1, 2) і дотикається до прямої у = х в точці (3, 3).

9. Визначити вид поверхні та знайти її найпростіше рівняння:

2x² – 3y² + 5z² – 4x – 6y + 10z – 2 = 0.

10. Зясувати геометричний зміст рівняння та побудувати ескіз 5x² – 6z² = 30.

Варіант 7.

1. Нехай а і b – сторони ромба, які виходять із спільної вершини. Довести, що діагоналі ромба взаємно перпендикулярні.

2. Через точку перетину прямих 2х – 5у – 1 = 0 і х + 4у – 7 = 0 провести пряму, яка ділить відрізок між точками А(4, 3) і В(-1, 2) у відношенні = 2 : 3.

3. Скласти рівняння сторін трикутника, знаючи одну з його вершин А(-4, 2) і рівняння двох медіан 3х – 2у + 2 = 0 і 3х + 5у – 12 = 0.

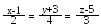
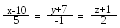4. Через точку А(4, 0, -1) провести пряму так, щоб вона перетинала дві прямі:

та .

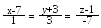
5. Знайти відстань точки А(3, 5, -1) від прямої .

6. Знайти точку, симетричну точці А(7, 6, -1) відносно площини

2х + 4у – z +17 = 0.

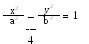
7. На еліпсі знайти точку, для якої добуток фокальних

радіусів-векторів дорівнює квадрату малої півосі.

8. Через точку М(2, -1) провести коло, що дотикається до кола

х² +у² –8х –4у+19 = 0 і має радіус, рівний одиниці.

8. Визначити тип поверхні та знайти її найпростіше рівняння:

2х² – 4у² + 6х + 8у – 10z – 5 = 0.

10. Зясувати геометричний зміст рівняння та побудувати ескіз:

4у² – 3х² + 5z² – 6 = 0

Варіант 8.

1. На сторонах трикутника АВС поза ним побудовані рівносторонні трикутники АВС₁, ВСА₁, САВ₁. Довести, що АА₁ + ВВ₁ + СС₁ = 0.

2. Знаючи рівняння 3х – 2у + 6 = 0 однієї із сторін кута і рівняння його бісектриси х – 3у + 5 = 0, скласти рівняння другої сторони кута.

3. Обчислити площу ромба, знаючи одну із його вершин А(0, -1), точку перетину діагоналей М(4, 4) і точку (2, 0) на стороні АВ.

4. На відстані трьох одиниць від площини 3х – 6у – 2z + 14 = 0 провести площину, яка паралельна даній.

5. Скласти рівняння спільного перпендикуляра до прямих:

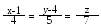
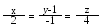
і .

6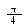. Скласти рівняння дотичної до параболи у² = 4х, яка утворює з прямою

х + у = 0 кут .

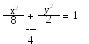
7. З точки (-2, 3) до еліпса проведено дві дотичні. Скласти рів-няння цих дотичних та визначити кут між ними.

1. С

   x = t

   y = 1 + 8t

   z = – 1 + 2t

   x = 1 + 4t

   y = 3 + 5t

   z = – t

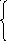
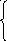   класти рівняння прямої, яка проходить через точку (-3, 2, 1) і перпендикулярна до двох прямих:

і .

2. Визначити вид поверхні та знайти її найпростіше рівняння:

3х² – 8у + 6z² – 3z + у² – 1 = 0.

10. З'ясувати геометричний зміст рівняння та побудувати ескіз: 3х² – 4z² = 12.

Варіант 9.

1. Нехай точка О – точка перетину медіан трикутника АВС і АО =a, АС = b. Розкласти АВ і ВС за векторами а і b.

2. Трикутник АВС заданий координатами своїх вершин А(1, -2); В(4, 2); С(13, 3). Написати рівняння прямої, яка містить бісектрису внутрішнього кута А.

3. Скласти рівняння прямої, яка проходить через точку перетину прямих 2х + у – 2 = 0 і х – 5у – 23 = 0 та ділить навпіл відрізок АВ, де А(5, -6); В(-1, 4).

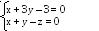
4. Знайти рівняння прямої, що проходить через дану пряму і

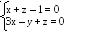
парале льна прямій .

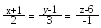
5. На прямій знайти точку, яка була б рівновіддалена від

двох площин 12х – 9у + 20z – 1 = 0 і 16х +12у – 15z + 2 = 0.

6. З даної точки А(1, 2, -3) опустити препендикуляр на пряму , знайти його рівняння та довжину.

7. Знайти рівняння кола, центр якого в точці (0, 1) і яке дотикається до гіперболи 2х² – у² = 1.

8. Скласти рівняння хорди параболи у² = 4х, яка в точці (3, 1) ділиться навпіл.

9. Визначити вид поверхні та знайти її найпростіше рівняння:

3х² + 6х + 3у² – 12у + 3z² – 15z – 5 = 0.

10. З'ясувати геометричний зміст рівняння та побудувати ескіз: 3у² – z² = 5.

Варіант 10.

1. УтетраедріABCD дано ребра АВ = b; АС = с; AD = d. Виразити через ці вектори решту ребер тетраедра, медіану DM грані BCD, вектор АО, де О – центр ваги грані BCD.

2. Довести, що бісектриси кутів між прямими х –2у – 2 = 0 і 4х + 3у – 12 = 0 взаємно перпендикулярні.

3. Через точку (1, -1) провести пряму так, щоб середина її відрізка між прямими х + 2у – 1 = 0 і х + 2у – 3 = 0 лежала б на прямій х – у – 1 = 0.

4. Скласти рівняння площини, що проходить через точки (2, 0, 0); (0, 3, 0); (0, 0, 6) та визначити відстань точки (3, -1, 5) від цієї площини.

5. Через дану точку М(1, 0, 1) провести пряму так, щоб її відрізок між площинами х – 2у + 2z – 1 = 0 і 2х – 4у + 4z – 3 = 0 ділився б у відношенні

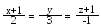
1 : 2 точкою перетину з прямою .

6. Знайти рівняння кола, що проходить через точку (3, 1) і дотикається до еліпса 3х² + у² = 7 в точці (1, 2).

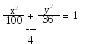
7. На еліпсі знайти точку, відстань якої від правого фокуса у

чотири рази більша відстані її від лівого фокуса.

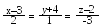
8. Знайти рівняння площини, яка проходить через пряму

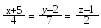
і па ралельна прямій .

9. Визначити вид поверхні та знайти її найпростіше рівняння:

2у² – 8у + 3х – 4z + 12z² – 3 = 0.

10. З'ясувати геометричний зміст рівняння та побудувати ескіз:

5у² – 6х + 15 = 0.