§3. Формула Ньютона-Лейбница.

Пусть функция y = f(x) интегрируема на отрезке [a, b].

Теорема. Если функцияy = f(x)непрерывна на отрезке [a, b] иF(x) какая-либо ее первообразная на этом отрезке(F (x)= f(x)), то имеет место формула

(1).

Доказательство:

Точками разобьем отрезок [a,b] наn частичных отрезков

x

a=x₀ x1 x2 xi-1 xi b=x_n

Рассмотрим тождество: F(b) – F(a) = F(x_n) – F(x₀) = (F(x_n) – F(x_n-1)) + (F(x_n-1 – F(x_n-2)) + . . . +(F(x₁) – F(x₀)).

К каждой разности в скобках применим формулу Лагранжа: f(b) – f(a) = f (c)(b – a).

Получим:

F(b) – F(a) = F (c_n)(x_n – x_n-1) + F (c_n-1)(x_n-1 – x_n-2) + . . .+ F (c₂)(x₂ – x₁) + F (c₁)(x₁ – x₀) =

_{n n n}

 F (c_i)(x_i – x_i-1) =  f(c_i)(x_i – x_i-1) , т. е. F(b) – F(a) =  f(c_i)(x_i – x_i-1) (2), где c_i – некоторая ^{I=1 I=1 I=1}

точка интервала (x_i-1; x_i).Т. к. функцияy = f(x) непрерывна на [a, b], то она интегрируема на этом отрезке. Поэтому существует предел интегральной суммы, равный определенному интегралу отf(x)на отрезке [a, b].

Перейдем в равенстве (2) к пределу при n   (  0), получим, т. е.. Ч.т.д.

Равенство (1) называется формулой Ньютона-Лейбница.

_b

Разность F(b) – F(a) обозначают следующим образом:F(x)_a и формулу (1) в этом случае можно переписать

.

Формула (1) дает удобный способ вычисления определенного интеграла:

• надо найти первообразную подинтегральной функции – F(x);

• посчитать разность значений этой первообразной на концах отрезка [a, b] –F(b) – F(a).

Примеры.

1). ;

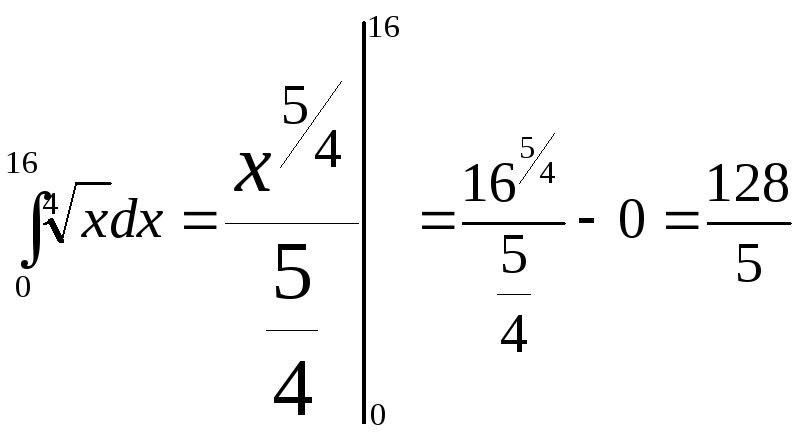2). .

§4. Основные свойства определенного интеграла.

1. Постоянный множитель можно выносить за знак определенного интеграла:

, гдеk = Constиf(x)– функция, интегрируемая на [a,b].

Доказательство.

Составим интегральную сумму для функции kf(x): , тогда .

2. Определенный интеграл от алгебраической суммы конечного числа функций, интегрируемых на [a, b], равен сумме интегралов от этих функций:

.

Доказательство.

3. Если поменять местами пределы интегрирования, то знак интеграла изменится на противоположный:

.

Это свойство можно доказать по определению определенного интеграла (аналогично свойствам 1 и 2). Оно подтверждается формулой Ньютона-Лейбница:

.

4. Определенный интеграл по всему отрезку интегрирования равен сумме интегралов по частям этого отрезка (аддитивность определенного интеграла):

Доказательство.

При разбиении отрезка [a, b] на части включим точкусв число точек деления (это можно сделать, т.к. интегральная сумма не зависит от способа разбиения отрезка [a, b] на части). Еслиc = x_m, то интегральную сумму можно разбить на две суммы:

. (*)

Каждая из сумм в равенстве (*) является интегральной суммой функции f(x)соответственно для отрезков [a, b], [a, с] и [с, b]. Переходя к пределу в равенстве (*) приn   (0), получим.

5. Теорема о среднем. Если функция f(x) непрерывна на [a, b], то существует такая точка c  (a, b), что .

Доказательство.

По формуле Ньютона-Лейбница имеем , гдеF(x) = f(x). Применяя к разностиF(b) – F(a) формулу Лагранжа (теорему о конечном приращении функции), получимF(b) – F(a) = F(c)(b – a) = f(c)(b – a).

Геометрический смысл теоремы о среднем:Еслиf(x)  0, то значение определенного интеграла равно площади прямоугольника с высотойf(c)и основаниемb – a, гдеc  (a, b).

y

y = f(x)

a 0 c b

Число называетсясредним значениемфункцииf(x) на отрезке [a, b].

6. Если функция f(x) сохраняет знак на отрезке [a, b](a < b), то интеграл

имеет тот же знак, что и функция.

Доказательство.

Пусть f(x)  0на отрезке [a, b], тогда по теореме о среднем , гдеc  (a, b). Но, т.к.f(x)  0при x [a, b], то иf(с)  0иb – a > 0, поэтомуf(c)(b – a)  0.

7. Неравенство между непрерывными функциями на отрезке [a, b](a < b) можно интегрировать (в отличие от дифференцирования – дифференцировать неравенства нельзя).

Например, если f₁(x)  f₂(x) при x [a, b], то

Доказательство.

Т.к. f₂(x) – f₁(x)  0 (приa < b), то по свойству 6, имеем или по свойству 2: , т.е. .