Геометрический смысл полного дифференциала.

Для функции одной переменной y = f(x)в точкеx₀ геометрический смысл дифференциала означает приращение ординаты касательной, проведенной к графику функции в точке с абсциссойx₀при переходе к точкеx₀ + Dx. А дифференциал функции двух переменных в этом плане является приращениемаппликатыкасательнойплоскости, проведенной к поверхности, заданной уравнениемz = f(x,y), в точкеM₀(x₀, y₀) при переходе к точкеM(x₀ + Dx, y₀ + Dy).Дадим определение касательной плоскости к некоторой поверхности:

Определение.Плоскость, проходящая через точкуР₀поверхностиS, называетсякасательной плоскостью в данной точке, если угол между этой плоскостью и секущей, проходящей через две точкиР₀иР(любая точка поверхностиS), стремится к нулю, когда точкаРстремится по этой поверхности к точкеР₀.

Пусть поверхность Sзадана уравнениемz = f(x,y).Тогда можно показать, что эта поверхность имеет в точкеP₀(x₀, y₀, z₀)касательную плоскость тогда и только тогда, если функцияz = f(x,y)дифференцируема в этой точке. В этом случае касательная плоскость задается уравнением:

z – z₀ = + (6).

Следовательно, приращение Dzаппликаты касательной плоскости определяется формулой:

Dz = + , что совпадает с формулой полного дифференциала функции двух переменных.

§5. Производная по направлению, градиент функции.

Частные производные функции y=f(x₁,x₂..x_n)по переменнымx₁, x₂ . . . x_n выражают скорость изменения функции по направлению координатных осей. Например,есть скорость изменения функции пох₁ – то есть предполагается , что точка, принадлежащая области определения функции, перемещается лишь параллельно осиОХ_1, а все остальные координаты остаются неизменными. Однако, можно предположить, что функция может изменяться и по какому-нибудь другому направлению, не совпадающему с направлением какой либо из осей.

Рассмотрим функцию трех переменных: u=f(x,y,z).

Зафиксируем точку М₀(x₀,y₀,z₀)и какую-нибудь направленную прямую (ось)l, проходящую через эту точку. ПустьМ(x,y,z) - произвольная точка этой прямой иêМ₀Мê- расстояние отМ₀доМ.

Du = f (x,y,z) – f(x₀,y₀,z₀)– приращение функции в точкеМ₀.

Найдем отношение приращения функции к длине вектора :

Определение.Производной функцииu = f (x,y,z)по направлениюl в точкеМ₀называется предел отношения приращения функции к длине вектораêМ₀Мêпри стремлении последнего к 0 (или, что одно и то же, при неограниченном приближенииМкМ₀):

(1)

Эта производная характеризует скорость изменения функции в точке М₀в направленииl.

Пусть ось l (векторМ₀М) образует с осямиOX, OY, OZуглысоответственно.

Обозначим x-x₀= ;

y-y₀ = ;

z-z₀ = .

Тогда вектор М₀М = (x - x₀, y - y₀, z - z₀)= и его направляющие косинусы:

;

;

.

Отсюда получаем следующие выражения для Dx, Dy, Dz:

(2)

Полное приращение функции в точкеМ₀:

можно представить в виде:

(3), где

Подставим выражения (2) в (3):

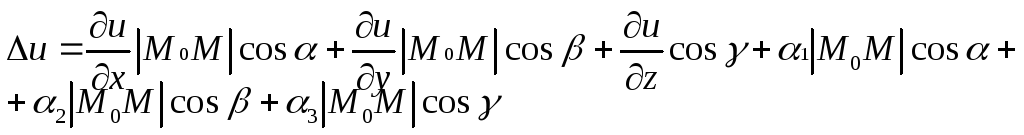
Найдем отношение :

Перейдем к пределу при êМ₀М ê® 0:

(4).

(4) – формула для вычисления производной по направлению.

Конечно, направление может быть задано просто соответствующим вектором. Рассмотрим вектор, координатами которого являются частные производные функции u=f(x, y, z)в точкеМ₀:

grad u - градиент функцииu=f(x, y, z)в точке М(x, y, z)

Рассмотрим единичный вектор по направлению l - - это вектор, длина которого равна 1,а направление совпадает с направлением осиl.

Тогда производная функции u=f(x, y, z) по направлениюlможет быть представлена как скалярное произведение():

.

Следовательно, производная функции u=f(x, y, z)по данному направлениюlесть скалярное произведение градиента функции на единичный вектор этого направления.