
1.Мн-во- совок-ть объектов, предметов, кот объединены на основ. к-н признака(мн нат. чисел). Объекты из кот состоят мн-ва –наз-ся его элемент. Мн-во обозн. большими буквами лат алфав.: А,B,Cа его элементы – малыми: a,b,c,d. Мн-во, кот не содержит ни 1-го элемента наз пустым. Мн-ва быв-т конеч-е(мн однозн.ч. и бескон-е(мн нат. чис).Мн-во м/задать 1-м из способов:перечислен. и указание характ-его св-ва элем. мн. Два мн назыв. Равными если они содерж. одни и теже элементы.Мн-во В наз. подмн. мн А если каждый элемент мн В явл. также и элем. мн А.Пустое мн явл. подмн. любого мн. Любое мн явл подмн. самого себя.Если мн не имеют общих элем то говорят что они непересек.А если имеют хотя бы один общий элем –пересекаются. Мн-во наз-ся универс-ым, если все мн-ва явл его подмн-ми. Пересеч-м мн-в А и В наз-ся мн-во, кот состоит из тех и только тех элементов, кот одноврем-но принадлежат и мн А и мн В. Объедин. мн-в А и В наз-ся мн, кот состоит из тех и только тех элементов, кот входят хотя бы в одно из мн-в А или В. Законы пересеч-я мн: 1) коммутат (перемест-й)А В=В А(док. след из опред.)2) ассоциативный А В С= А В С(док. на круг эйлера) позволяет находить пересеч-я 3-х и более мн-в, а также записывать выражения без скобок. 3)А А=А, А Ǿ=Ǿ,А И=А, ВcА,А В=В.Зак объедин.: 1) 2) 3)АUА=А, АUО=А, АUИ=И,ВcА, АUВ=А. 4) дистрибут. (пересеч-е относительно объедин-я) АU(В С)=(АUВ) (АUС) б)А (ВUС)=(А В)U(А С)
2. Вычит мн-в.Разностью мн-в a и b наз-ся мн, состоящее из всех тех и только тех мн-в а, кот не принадлежат мн-ву b. Разность мн-в обозн. \.Св-ва:1.А/(В С)= (А/В)U (А/С). 2.А/(ВU С)=(А/В) (А/С)=А/В/С.Д-во1:1)х€А/(В С)х€А^хне€В Сх€А^ (х€В или х€С(х€А^х не€В) или( х€А^х не€С)(х€А^х не€С)( х€А/В)или (х€А/С) х€(А/В) U(А/С) 2)х€(А/В)U(А/С)х€(А/В)или х€(А/С) (х€В^х не€В) или(х€А^х не€С) х€А^(х не€В или х не€С)х€А^(х не€В С)х€А/(В С) .Пусть В явл подмн-м А,мн всех элементов А кот не принадл. мн В наз-ся дополнен. мн В до мн А и обозн. А’а. Дополн. мн В до универс-го мн обозн. В'. Св-ва: (АВ)ꞌ=АꞌUВꞌ. 2.(АUВ)ꞌ=Аꞌ Вꞌ. Декартово произв-е 2х мн-в. Каждый элемент входит во мн-во только 1 раз,при этом порядок записи элементов м/б разным. Однако,часто приходится учитывать и порядок в кот наход-ся данные элементы (напр, 742 и 427-мн-во цифр одинаково, а числа разные). Вводится новое понятие кортеж-конечная упорядоченная последоват-ть (кот допускает повторение) элементов к-н мн-ва. Кол-во элем. в кортеже назыв. его длиной, а сами элем. компонентами кортежа.(а,в,с)-элем3. 2 кортежа назыв.равными, если имеют одинак. длину и их соотв-е компоненты равны. Декарт призв-е св-ва. Декарт-м призвед-м 2х мн-в а и b наз-ся мн пар, первые компоненты кот. принадлеж. мн а, а вторая мн. b. Св-ва: 1) декатрово произвед-е 2 мн-в не коммутативно (нельзя переставлять мн-ва а и b (а;в)=(в;а) 2) дек-во произв. не ассоциативно 3) дистрибут-й з-н относительно операций пересеч, объедин, разности мн-в как слева, так и справа выполн.а) Ах(ВUС)= (АxВ)U(АxС)б)Аx(В С)=(АxВ) (АxС). в)Аx(В/С)= (Аx В)/(АxС)
3.Комбин-ой
задачи.Раздел
матем., кот рассматр-т задачи,связан-е
с комбиниров-м элем. мн. наз-т комбинаторикой.
В основе всей теории лежат 2 осн правила:
прав-ло суммы и произвед-я. Правило +
позволяет найти число элем. в объедин
2х или неск-х мн, кот не пересек-ся.
Комбинат-е правило +: если выбор одного
объекта м/осущ-ть Р1-различными
способами,Р2-различ.способ., отличных
от предыдущ-го и т д, то выбор к-н одного
объкта из все данных объектов м/осущ-ть
Р1+Р2+…Рк. спос-ми. Правило нахожд-я элем.
декартово* в комбин-ке наз-ся правилом
*: Если 1-й элемент м/выбрать m1
сп-ми, после этого 2-й элемент м выбрать
m2
сп-ми и т д.,n-й
элемент м/выбрать mn
спос-ми, то упорядоченну n-ку
элем. м/выбрать m1*m2…
способами. Мн наз. упорядоч-м,если его
элементы расположены в определ-м порядке.
В уроряд-м мн все элем. различные.Различ-е
упорядоч-я 1-го и того же мн состоят из
одних и тех же элементов и отлч-ся лишь
порядком элементов. Перестан-й
без повтор-й
наз всякое упорядоченное мн-во. Теорема:
кол-во ПбП n-элем-го
мн вычесл. по формуле Рn=n!,
n!-
n-факториал,
n!-произвед-е
все натур. ч. от 1 до n
(1, 2, 3… n)
(напр. 3! – 1*2*3=6.). Размещение
без повтор
наз. каждое упорядоч-е к-элементное
подмн-во данного n-элем-го
мн-ва. Теорема:кол-во размещений из
n-элем
по к-элем опред. по формуле. A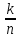 =
=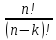 .(Сколько
4-хзначных натур. чисел м/составить из
различных цифр 1,2,4,5,8,9. Нам необх. Найти
сколько 4-хзначн. Упорядочных подмножеств
м/ составить из 6-элемн.
мн.А4.6=6!/(6-4)!=6!/2!=1*2*3*4*5*6/1*2=3*4*5*6=18*20=360Сочет.
без повтор
наз каждое К-элем подмн-во данного
n-элем-го
мн обознач Сn.
Теорема: кол-во сочет. без повторений
из n-элем
по к-элем вычисл. по формуле С
.(Сколько
4-хзначных натур. чисел м/составить из
различных цифр 1,2,4,5,8,9. Нам необх. Найти
сколько 4-хзначн. Упорядочных подмножеств
м/ составить из 6-элемн.
мн.А4.6=6!/(6-4)!=6!/2!=1*2*3*4*5*6/1*2=3*4*5*6=18*20=360Сочет.
без повтор
наз каждое К-элем подмн-во данного
n-элем-го
мн обознач Сn.
Теорема: кол-во сочет. без повторений
из n-элем
по к-элем вычисл. по формуле С .
Кол-во упорядоченных к-элем-х подмн-в
данногоn-элем-го
мн выч по формуле A
.
Кол-во упорядоченных к-элем-х подмн-в
данногоn-элем-го
мн выч по формуле A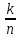 =
= . Тогда кол-во неупоряд-х подмн-в будет
в к! раз меньше, чем кол-во упорядоченных
т к из каждого неупоряд-го подмн-ва кот
содержит к-элементов м составить
к-факториал упорядоч-х подмн-в. Т. о.
С
. Тогда кол-во неупоряд-х подмн-в будет
в к! раз меньше, чем кол-во упорядоченных
т к из каждого неупоряд-го подмн-ва кот
содержит к-элементов м составить
к-факториал упорядоч-х подмн-в. Т. о.
С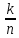 =
= =
=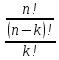 =
=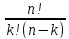 (Сколькими м/выбрать 3ленты разных цветов
из 6лент разных цветов.Реш. т.к. порядок
выбор лент не имеет значение то в задаче
речь идет о з элем подм 6 элем мн. т.е
сочет без повторения
С3.6.=6!/(6-3)!3!=1*2*3*4*5*6/1*2*3*1*2*3=20Размещ.
с повтор
наз кортеж длины К составленный из
n-элементного
мн (k
м/б
(Сколькими м/выбрать 3ленты разных цветов
из 6лент разных цветов.Реш. т.к. порядок
выбор лент не имеет значение то в задаче
речь идет о з элем подм 6 элем мн. т.е
сочет без повторения
С3.6.=6!/(6-3)!3!=1*2*3*4*5*6/1*2*3*1*2*3=20Размещ.
с повтор
наз кортеж длины К составленный из
n-элементного
мн (k
м/б
 n).
Кол-во размещ-й из n-элем
по к обозн-ся
n).
Кол-во размещ-й из n-элем
по к обозн-ся
 .
Теорема: кол-во размещ-й с повторен-ми
изn-элем
выч-ся по формуле
.
Теорема: кол-во размещ-й с повторен-ми
изn-элем
выч-ся по формуле
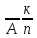 =nk.
Перестановки
с
повтор-ми наз любой кортеж длины n
n-элем-го
мн. Обозн-ся
=nk.
Перестановки
с
повтор-ми наз любой кортеж длины n
n-элем-го
мн. Обозн-ся
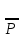 n.
Теорема: кол-во различных перестановок
с повтор-ми n-элем
мн, в кот один из элементов повтор-ся n1
раз, 2-й элемент n2
раз и т д, К- элемент повтор nk
раз вычисл по формуле
n.
Теорема: кол-во различных перестановок
с повтор-ми n-элем
мн, в кот один из элементов повтор-ся n1
раз, 2-й элемент n2
раз и т д, К- элемент повтор nk
раз вычисл по формуле
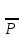 n=
n=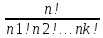 .
Л1и1т2е1р2а2ту1ра.не А10=10!/ 1!1!2!1!2!2!1! =453600
.
Л1и1т2е1р2а2ту1ра.не А10=10!/ 1!1!2!1!2!2!1! =453600
4. Высказывание- предл-е относит-но которого м/утверждать истинно оно или ложно. Конъюнкц. выск-й А и В наз составное высказ-е А и В истинное тогда и т т, к оба высказ-я А и В истинны и ложно если хотя бы 1-но из высказ-й ложно. Обозн-ся ˄ . М/находить конъюнкцию 3 или несколько высказ. Она будет истина т и т т, если одновременно истинны все высказывания, кот входят в нее. Дизъюнкц.высказ-й А и В наз высказ-е А или В, кот явл истинным, если хотя бы одно из высказ-й и ложным-если оба высказывания ложны обозн-ся А ˅ В. Законы: 1) коммуник.(перемест.)з-н А˄В=В˄А; А˅В=В˅А; 2) ассоциат. А˄(В˄С)=(А˄В)˄С; А˅(В˅С)=(А˅В)˅С; (таб. больш.)3) а) дистрибут з-н коньюнкции относит-но дизьюнкции А˄(В˅С) =(А˄В)˅(А˄С); б) дистрибу з-н дизьюнкции относит-но коньюнкции А˅(В˄С)=(А˅В)˄(А˅С);(таб) 4) А˄А=А; А˅А=А; А˄И=А; А˅И=А; А˄Л=Л; А˅Л=А.
5.
Отрицание, импликация .Отрицанием
высказыв-я А наз-ся высказ-е «не А», кот
явл истенным, если А-ложно и ложным, если
А-истенно, обозн-ся
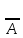 (не правда, что А). Импликацией- высказыв-е,
«если А,то В» ложно т и т т, если А-истинно,
а В-ложно, в остальных случаях импликация
истинна. Обозн
(не правда, что А). Импликацией- высказыв-е,
«если А,то В» ложно т и т т, если А-истинно,
а В-ложно, в остальных случаях импликация
истинна. Обозн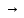 .
Виды: 1) А
.
Виды: 1) А В-прямая;
2) В
В-прямая;
2) В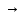 А-обратная
данной (меняем местами условие и
заключение); 3) Из
А-обратная
данной (меняем местами условие и
заключение); 3) Из -
противопол-я данной(строим отрицание
условия и заключения в прямой теореме);
4) Если
-
противопол-я данной(строим отрицание
условия и заключения в прямой теореме);
4) Если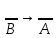 -
обратная противоположной.Эквиваленцией
наз составное высказыв-е А т и т т , когда
В, оно истинно, если оба высказывания
истинны или оба ложны и ложно, во всех
остальн. случ.. Закон для отрицания
высказ.: 1) закон двоиного отрицания
(А=
-
обратная противоположной.Эквиваленцией
наз составное высказыв-е А т и т т , когда
В, оно истинно, если оба высказывания
истинны или оба ложны и ложно, во всех
остальн. случ.. Закон для отрицания
высказ.: 1) закон двоиного отрицания
(А=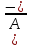 );
2) з-н противоречия А
);
2) з-н противоречия А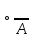 =Л;(показ
что выск. Не м/*быть одноврем ист. и л.
3) з-н исключения третьего А˅
=Л;(показ
что выск. Не м/*быть одноврем ист. и л.
3) з-н исключения третьего А˅ =И;
4) з-н де Моргана а)
=И;
4) з-н де Моргана а) =
= ˅
˅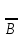 ;(таб)
б) А˅В=
;(таб)
б) А˅В=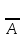 ˄
˄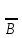 .
Законы для импликации: 1) з-н, кот связыв-т
импликацию с отрицат и дизьюнкцией
высказываний.А
.
Законы для импликации: 1) з-н, кот связыв-т
импликацию с отрицат и дизьюнкцией
высказываний.А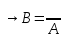 ˅В;
2) з-н контрапозиции А
˅В;
2) з-н контрапозиции А В=
В=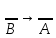 ;
З-н эквиваленции связывает коньюнкцию
импликации А
;
З-н эквиваленции связывает коньюнкцию
импликации А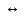 В=(А
В=(А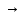 В)˄(В
В)˄(В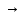 А).
А).
6.
Понятие
Предикат-это предл-е с одной или
несколькими перемен-ми кот при конкрет-х
значениях перемен-х превращ-ся в
высказыв-е. По числу переменных, входящих
в предикат выд.: одноместныеА(х),
двуместныеА (х;у). С каждым предик. связаны
2 мн:область определения предиката
(обознач-ся х-это мн-во тех значений
переменной, при кот предикат обращ в
высказывание); 2-мн-во истинности
предиката-это мн-во тех знач переменной
из области определения при кот предикат
превращается в истинное высказывание
Т(напр. А(х):х кратно 5. Х=Nобласть
определ.Т=5,10,15,20…-мн. истен. Предик). 2
предиката А(х) и В(х) заданные на одном
и том же мн-ве х наз-ся равносильным
(эквивалентным), если они имеют одно и
тоже мн-во истинности и запис-ся
А(х) В(х).(напр
А(х):х+2=4, х
В(х).(напр
А(х):х+2=4, х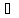 N;
В(х):
N;
В(х):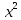 -4=0,х
-4=0,х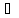 N.
N.
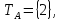
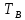 =
= ,
,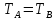
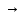 А(х)
А(х) В(х)).
Предик: элементные, составные. Состав-е
образовыв-ся из элементарных при помощи
логически связанных высказываний.Отрицанием
предиката А(х) наз-ся предикат не А
от(х),заданый на том же мн х, он истинен
при тех значениях, при кот предикат А(х)
ложен. Тне а^в= Т͞аv͞͞͞
͞в=Т͞а U͞
͞в=Та ꞌU
вꞌ. Конъюнкцией А(х) и В(х) наз-ся составной
предикат А(х) и В(х) заданный на том же
мн-ве х. Он истинен когда одновременно
истинны оба предиката А(х) и В(х). Истенность
конъкций явл его пересечение. Дизъюнкцией
наз-ся
составной предикат А(х) и В(х) задан на
том же мн-ве х.. он истинен х
В(х)).
Предик: элементные, составные. Состав-е
образовыв-ся из элементарных при помощи
логически связанных высказываний.Отрицанием
предиката А(х) наз-ся предикат не А
от(х),заданый на том же мн х, он истинен
при тех значениях, при кот предикат А(х)
ложен. Тне а^в= Т͞аv͞͞͞
͞в=Т͞а U͞
͞в=Та ꞌU
вꞌ. Конъюнкцией А(х) и В(х) наз-ся составной
предикат А(х) и В(х) заданный на том же
мн-ве х. Он истинен когда одновременно
истинны оба предиката А(х) и В(х). Истенность
конъкций явл его пересечение. Дизъюнкцией
наз-ся
составной предикат А(х) и В(х) задан на
том же мн-ве х.. он истинен х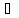 Х
тогда, когда хотя бы 1-н из предикатов
истинен. А(х)
Х
тогда, когда хотя бы 1-н из предикатов
истинен. А(х)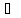 В(х)Импликацией
наз-ся
составной предикат А(х)
В(х)Импликацией
наз-ся
составной предикат А(х)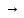 В(х),
ели А(х), то В(х) задан на том же мн-ве х.
он ложен когда А(х)-И, а В(х)-Л, при остальных
И.Тав=ТаꞌUТв
Эквиваленцией
наз-ся составной предикат А(х)
В(х),
ели А(х), то В(х) задан на том же мн-ве х.
он ложен когда А(х)-И, а В(х)-Л, при остальных
И.Тав=ТаꞌUТв
Эквиваленцией
наз-ся составной предикат А(х)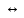 В(х),
х
В(х),
х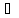 Х.
Истинно только когда оба И или оба Л,
при остальных ложно. Тав=(Та
Тв)U(Таꞌ
Твꞌ)
Х.
Истинно только когда оба И или оба Л,
при остальных ложно. Тав=(Та
Тв)U(Таꞌ
Твꞌ)
7.
Матем-е понятия.
Объем понятия- мн-во объектов, обозначаемых
одним и тем же термином. Если объем
понятия А явл частью объема понятия В
(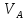 )
) )
то понятие А наз-т видовым по отнош-ю к
понятию В, а понятие В родовым по отнош
к В (напр. Понятие ромб явл видовым
понят-м параллелограмма, а понятие
параллелограмм это родовое понятие для
ромба). Содерж-е понятия-это совокупность
св-в данного понятия. М/у объемом и
содерж-м понятия сущ-т связь:чем больше
объем понятия, тем меньше его содержание.
Чем больше содержание тем меньше его
объем. Понятие-указание сущест. св-в
объекта,кот достаточн. для распозн.
объекта..Осн
сп-бы определ. понятий:
1) определ. понятия
ч/з род и видовое отличие.
При этом СП-бе указыв-ся более общее
родовое понятие, а затем указыв-ся
видовое отличие, то св-во кот выделяет
данный вид из др. видов данного рода.
(напр. Квадрат=это прямоугол, у кот все
стороны равны);2) генетические.-указывает
на происхождение понятий (сфера,
окружность…); 3) аксиоматический
сп-б-определ. понятия ч/з с-му аксиом; 4)
индуктивный- сп-б получения все элем.
понятия арифм и геометр прогрессии; 5)
контекстуальные-определение понятия
ч/з текст; 6) Остенсивные - определения
понятия ч/з демонстрацию. Требования к
опред понятий: 1) определяемое и
определяющее понятие д/б соразмерным
(их объемы д/б равны); 2) в определении
понятия д/б указаны св-ва, кот позволяют
выделить данный объект среди мн-ва др
объектов; 3) отсутствие в отрицании
избыточности; 4) запрещается порочный
круг. Нельзя определить понятие ч/з само
себя или понятие определить ч/з другое
ч/з первое; 5) определяемый объект д
существовать.
)
то понятие А наз-т видовым по отнош-ю к
понятию В, а понятие В родовым по отнош
к В (напр. Понятие ромб явл видовым
понят-м параллелограмма, а понятие
параллелограмм это родовое понятие для
ромба). Содерж-е понятия-это совокупность
св-в данного понятия. М/у объемом и
содерж-м понятия сущ-т связь:чем больше
объем понятия, тем меньше его содержание.
Чем больше содержание тем меньше его
объем. Понятие-указание сущест. св-в
объекта,кот достаточн. для распозн.
объекта..Осн
сп-бы определ. понятий:
1) определ. понятия
ч/з род и видовое отличие.
При этом СП-бе указыв-ся более общее
родовое понятие, а затем указыв-ся
видовое отличие, то св-во кот выделяет
данный вид из др. видов данного рода.
(напр. Квадрат=это прямоугол, у кот все
стороны равны);2) генетические.-указывает
на происхождение понятий (сфера,
окружность…); 3) аксиоматический
сп-б-определ. понятия ч/з с-му аксиом; 4)
индуктивный- сп-б получения все элем.
понятия арифм и геометр прогрессии; 5)
контекстуальные-определение понятия
ч/з текст; 6) Остенсивные - определения
понятия ч/з демонстрацию. Требования к
опред понятий: 1) определяемое и
определяющее понятие д/б соразмерным
(их объемы д/б равны); 2) в определении
понятия д/б указаны св-ва, кот позволяют
выделить данный объект среди мн-ва др
объектов; 3) отсутствие в отрицании
избыточности; 4) запрещается порочный
круг. Нельзя определить понятие ч/з само
себя или понятие определить ч/з другое
ч/з первое; 5) определяемый объект д
существовать.
8.
Уравнении. Пусть
f(х)
и g(х)-выражения
с 1й переменной, заданные на мн-ве х
предикатами вида f(х)=g(х),
заданный на мн-ве х наз-ся уравнением с
1й переменной. (напр. 2х+3=3х-8,х R).корнем
уравнения наз-ся значение переменной
из области определения при кот ур-ие
преврашается в истеное числовое
равенство. Решить уравнение, значит
найти мн корней этого ур.(напр.
1)х(х-3)(х+7)=0- ур.3корня.2)ур имеют бесконечн.
много корней /х/=х Т=[0+∞) Два ур
наз.f1(x)=g1(x)
и f2(x)=g2(x)
равносильн. на мн Х, если мн их решений
совпадает.(напр. 3х(х-5)=о и х2-5х=о (о;5)Теорема
1
о равенстве уравн. и следствия из них.
Если к каждой части уравн-я n
f(х)=g(х)
заданных на мн-ве х, прибавить одно и
тоже выражение с переменной, n(x),
заданное на том же мн-ве х, то получим
уравн-е f(x)+h(x)=g(x)+h(х)
равносильно данному. Следствие из
теорем: 1) к каждой части уравн-я м/прибавить
одно и тоже число; 2) слагаемы в уравн-и
м/ переносить из одной части ур. в другую
с противоположным знаком. Теорема
2.
Если каждую часть уравн-я f(х)=g(х)
заданного на мн х умножить или разделит.
на одно и тоже выраж. h(x)
заданного на том же мн Х и не равно 0, то
получим уравнение f(x)*h(x)=g(x)*h(х)
равносильно первому. Следствие: обе
части уравн-я м умножить или разделить
на одно и тоже число, отличное от нуля,то
получ. ур. исходное.
R).корнем
уравнения наз-ся значение переменной
из области определения при кот ур-ие
преврашается в истеное числовое
равенство. Решить уравнение, значит
найти мн корней этого ур.(напр.
1)х(х-3)(х+7)=0- ур.3корня.2)ур имеют бесконечн.
много корней /х/=х Т=[0+∞) Два ур
наз.f1(x)=g1(x)
и f2(x)=g2(x)
равносильн. на мн Х, если мн их решений
совпадает.(напр. 3х(х-5)=о и х2-5х=о (о;5)Теорема
1
о равенстве уравн. и следствия из них.
Если к каждой части уравн-я n
f(х)=g(х)
заданных на мн-ве х, прибавить одно и
тоже выражение с переменной, n(x),
заданное на том же мн-ве х, то получим
уравн-е f(x)+h(x)=g(x)+h(х)
равносильно данному. Следствие из
теорем: 1) к каждой части уравн-я м/прибавить
одно и тоже число; 2) слагаемы в уравн-и
м/ переносить из одной части ур. в другую
с противоположным знаком. Теорема
2.
Если каждую часть уравн-я f(х)=g(х)
заданного на мн х умножить или разделит.
на одно и тоже выраж. h(x)
заданного на том же мн Х и не равно 0, то
получим уравнение f(x)*h(x)=g(x)*h(х)
равносильно первому. Следствие: обе
части уравн-я м умножить или разделить
на одно и тоже число, отличное от нуля,то
получ. ур. исходное.
9.
Нер-ва
с одной перемен. наз.предикатом вида
f(х)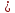 g(х)
(f(х)
g(х)
(f(х)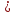 g(х))
задан. на мн х Решить нер-ва f(х)
g(х))
задан. на мн х Решить нер-ва f(х)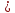 g(х)
наз мн значений х Х при постановке кот.
получается истенное числовое неравство.
Решить нерав.значит найти мн всех его
решений. 2 нер-ва наз равносильными, если
их мн решений совпадают. При решении
нерав. Польз. теоремами о равносильн.
Теорема
1:
Если в каждой части нер-ва f(х)
g(х)
наз мн значений х Х при постановке кот.
получается истенное числовое неравство.
Решить нерав.значит найти мн всех его
решений. 2 нер-ва наз равносильными, если
их мн решений совпадают. При решении
нерав. Польз. теоремами о равносильн.
Теорема
1:
Если в каждой части нер-ва f(х)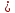 g(х)
заданного на мн прибавить одно и тоже
выражение с переменной h(x),
x
g(х)
заданного на мн прибавить одно и тоже
выражение с переменной h(x),
x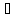 Х,
то получим нер-во f(x)+h(x)=g(x)+h(х)
равносильное исходному. Следст : 1) если
к каждой части нер-ва прибавить одно и
тоже число, то получим нер-во равносильное
данному; 2) члены нер-ва м/переносить из
1й части в другую с противопол-м знаком.
Теорема
2:
Если обе части нер-ва f(х)
Х,
то получим нер-во f(x)+h(x)=g(x)+h(х)
равносильное исходному. Следст : 1) если
к каждой части нер-ва прибавить одно и
тоже число, то получим нер-во равносильное
данному; 2) члены нер-ва м/переносить из
1й части в другую с противопол-м знаком.
Теорема
2:
Если обе части нер-ва f(х)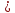 g(х)
заданного на мн-ве х умн.(разд.) на одно
и тоже выражение с переменной h(x)>0
заданное на том же мн-ве х ,то получим
нер-во f(x)*h(x)
g(х)
заданного на мн-ве х умн.(разд.) на одно
и тоже выражение с переменной h(x)>0
заданное на том же мн-ве х ,то получим
нер-во f(x)*h(x)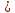 g(x)*h(х)
равносильное исходн. Следст: если обе
части нер-ва умн. на одно и тоже положит-е
действит. число, то получим нер-во
равносильное данному. Теорема
3
Если обе части нер-ва f(х)
g(x)*h(х)
равносильное исходн. Следст: если обе
части нер-ва умн. на одно и тоже положит-е
действит. число, то получим нер-во
равносильное данному. Теорема
3
Если обе части нер-ва f(х)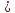 g(х)
заданного на мн-ве х умн.(разд.) на одно
и тоже выраж-е с переменной h(х)<0
заданного на том же мн-ве х , то получим
нер-во f(x)*h(x)
g(х)
заданного на мн-ве х умн.(разд.) на одно
и тоже выраж-е с переменной h(х)<0
заданного на том же мн-ве х , то получим
нер-во f(x)*h(x)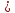 g(x)*h(х)
равносильно данному. Следст.: если обе
части нер-ва умн.(разд.) на одно и тоже
отрицат-е действ-е число и при этом знак
нер-ва поменять на противопол-й, получим
нер-во равносильное данному.
g(x)*h(х)
равносильно данному. Следст.: если обе
части нер-ва умн.(разд.) на одно и тоже
отрицат-е действ-е число и при этом знак
нер-ва поменять на противопол-й, получим
нер-во равносильное данному.
13.
Алгебра-ой
операцией в мн-ве х наз. отображение
(х:у)-> Z
кот. ставит в соответствие любой
упорядоченной паре (х,у) этого мн третий
эл-т Z
этого же мн. (напр.сложен. алг. опер. в мн
N.
Пусть х+у=Z,тогда(х;у)=Z,хуz
прин.N.2)+
не явл алг. опер в мн нечетн. чисел) Закон
коммутат: алгеб.
опер. наз. коммут. если рез-т ее применения
не зависит от порядка компонента, т.е.
для 2х эл-ов (а;в)€х вп-ся рав-во а*в=в*а.Закон
ассоциа-ти: алгеб.
опер. на мн-ве Х наз. ассоц-ой, если для
любых 3 эл-ов выпол-ся рав-во (а*в)*с=а*(в*с).
Закон
дистрибути: Ноль
это нейтральный эл-т относ-но опер-и
сложения, а 1- относ-но опера-и
умножения.а*(в+с)=а*в+а*с. Эл-т е из мн-ва
х наз. нейтральным
относ-но
операц-и *, если для любых эл-ов а€х
выпол. равен-во а*е=е*а =а. Поглощающий
эл-т: Число
0 отыгрывает особую роль не только
отно-но опер-и слож-я, но и относ-но опер-и
умнож-я. Говорят, что 0 явл. поглощ-м эл-ом
относ-но опер-и умнож-я.Пусть * алг. опер.
в мн х элем W
наз. поглощ. относит. данной операции
если для любых элем а мн Х вып. равенс.
А*W=W*а=W..
В мн Х не м/б 2-х различн. поглощ. элемен.
отн. опер.* Симметричный
эл-т: Пусть
во мн-ве х сущ. нейтрал. эл-т Е отно-но
опер-и * наз. элем.
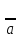 явл.симметр., а если выпол. рав-во
а*а=а*а=е.
явл.симметр., а если выпол. рав-во
а*а=а*а=е.
14. Преобразования плоскости.
Рассмотрим геометрич. преобр-ие, при кот. сохр-ся форма и размеры фигур, а меняется их расположение на плоскости. Такие преоб-я наз-ся перемещением. Определ-ие: Преобраз-ие плоскости при кот. кажд. Отрезок АВ переходит в равный ему отрезок А1В1 назыв. перемещением плоскости. Виды плоскости: 1) осевая симметрия с осью е наз-ся такое перем-е плоскости при кот. точки прям. Е отобрах-ся сами на себя а полуплоскости с границей е отобр-ся одна на другую.2) параллельный перенос- отображение плоск-ти на себя, при кот. все точки плос-ти перемещ-ся в одном и том же направлении на одно и то же расс-е. 3) поворот пло-ти- вокруг точки о наз-ся приоб-ие плос-ти, при кот. точеа о отобр-ся сама на себя, а произ-ся т.А плоскости отоб-ся в такую т. А1, что 1) <АОА1=Z, 2)АО=А1О Т. о наз-т центром поворота, если угол задан полож-м числом, то условились поворот произ-ть против часовой стре-ке, если отриц-й, то по часовой стрелке. 4) перемещение – центральной симметрией с центром О наз-ся поворот вокруг т. О на <180. В т. А и А1 лежат на одной прямой кот. прох-т через центрО и по разные стороны от центра: т.к. цент-я симметрия частный случай поворота, то она яв-ся перемещением.
15. Преобразование подобия с коэф Кне=о наз. такое преобразов. Плоск. При кот если А и В точки плоскости, А1 и В1 их прообраз при данном подобии то А1В1=К*АВ. (оставляющих неизменными только форму фигур. Св-ва подобия: 1) подобие с коэф-ом равной1-це явл. перемещением.Док-во:
2)Для подобия с коэф-ом К сущ-ет обратное подобие с коэф-ом 1/К. Док-во: пусть А и В разл. Точки плоск. А1В1=К*АВ,но т.к А=В, для данного подобия сущест.обратное такое что А1А В1В. 3)Композиция подобий есть подобие. Док-во: Пусть f1 ,f2 преобразов. подобий с коэф К1 и К2 выберем на плоскости произ. точки А и В. F1(A)=A1, f1(B)=B1 A1B1=K1*AB f2(A1)=A2, f2( B1)=B2 A2B2=K2*A1B1 A2B2=K2A1B1=K2*K1AB,значит композиц. f1◦f2 измен. расстоян. м/точками в К1*К2 раз,зн. явл. подобие.4)композиз. мн подобия образует группу. Одним из видов подобия явл. гомотетия. Опред-е: гомот-й с центром О и коэф-ом Кне=0 наз-ся приобраз-ие плоскости,облад. след. св-амиЕсли А точка плоск., А1-образ при данном приобразовании, то неОА1=К*неОА и обозн Нок Частные случаи гомотетии: 1) гомотетия с коэф-ом =1 яв-ся тождественным приобрет-ем Но1=Е.Док-во:неОА1=1неОА неОА1-неОА А1=А.2) гомотетия с коэф. К=-1 явл центральной симметрией .Но-1=Z0. 3)преоб. обратной гомотет. с коэф. К и цент. О явл гомотетией с коэф 1/К и цент О.
16. Теоретико-множественный смысл колич-го натур-го числа и нуля. Отношения равенства и неравенства на мн-ве целых неотриц-х чисел.
Колич-м натур. числом назыв. число, кот. показыв. ск-ко эл-ов содерж. в данном мн-ве. Пусть мн-во А и В таковы, что им соот-т одно и тоже число «а». n(А)=а, n(В)=а. Это значит, что их можно отобразить взаимооднозначно др. на др. и на один и тот же отрезок N ряда чисел. Два мн-ва, кот. можно взаимооднозначно отобразить др. на др. явл. равномощными=» для конечных мн-в утверждение: мн-во А равномощно мн-ву В=утверждению: мн-во А и В содер. одинак. кол-во эл-ов, т.е. им соотв-ет одно и тоже N число. Т.к. любому конеч. мн-ву соот-т лишь 1 N число, то вся сов-ть конеч. мн-в распа-ся на классы равномощных мн-в. Число а=в тогда и только тогда когда они опред-ся равномощ-ми мн-ми.Св-ва отношения «=»: 1) Рефлексивность а=а, 2) Симметричность если а=в, то в=а, 3) Транзитивность если а=в,в=с, то а=с. Отношение «<»: 1)Число а<в тода и только тогда, если мн-во А собственному подм-ву В1, мн-ва В и n(А)=а, n(В)=в. 2)Число а<в «=» когда сущ-ет N число с, такое что в=а+с 3)а<в,тогда и только тогда, когда отрезок N ряда чисел Nа явл. собств. подм-м отрезка N ряда чисел Nв. Св-ва:1) антирефлекс. а</а, 2) антиссиметр. a<в=»/в<а, 3) транзитивность а<в, в<с=»а<c. Т.о. отношение «<» явл. отношением строгого линейного порядка.
