48)Физический и математический маятники. Приведенная длина и центр качания физического маятника.
Математический
маятник
– материальная точка подвешенная на
длинной, тонкой, нерастяжимой, невесомой
нити. При отклонении маятника от положения
равновесия на материальную точку массой
m
действуют сила тяжести mg
и сила натяжения нити N.
Их равнодействующая F
направлена по касательной к окружности
радиусом R
и равна F=-mg
sin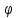
.
Период
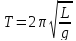
Физический
маятник –
абсолютно твердое тело имеющее ось
вращения не совпадающее с центром масс.
При отклонении физического маятника
от положения равновесия на угол
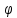возникает вращательный момент, стремящийся
вернуть маятник в положение равновесия.
Этот момент равен M=-mgl
sin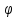
,
Где
m
–масса маятника, а l
– расстояние ОС между точкой подвеса
О и центром масс С маятника. Период
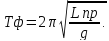Lпр
–
приведенная длина.
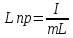I
– момент инерции.
Центр качания — точка, в которой надо сосредоточить всю массу физического маятника, чтобы его период колебаний не изменился.
Приведённая
длина вычисляется следующим образом:
где
I — момент
инерции относительно
точки подвеса, m — масса,
a — расстояние от точки подвеса до
центра масс.
49)Уравнение затухающих колебаний. Декремент затухания.
Затухающие
колебания —
колебания, энергия которых уменьшается
с течением времени. Свободные колебания
любого осциллятора рано или поздно
затухают и прекращаются. Поэтому на
практике обычно имеют дело с затухающими
колебаниями.
Они
характеризуются тем, что амплитуда
колебаний A является
убывающей функцией. Обычно затухание
происходит под действием сил сопротивления
среды, наиболее часто выражаемых линейной
зависимостью от скорости колеба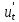ний 
или
её квадрата.
Уравнение
затухающих колебаний
-
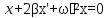
Декремент
затухания - количественная
характеристика быстроты затухания
колебаний.
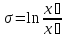
Декремент затухания – величина, обратная числу колебаний, по истечении которых амплитуда убывает в е раз. Напр., если б = = 0,01, то амплитуда уменьшится в е раз после 100 колебаний. Декремент затухания характеризует число периодов, в течение которых происходит затухание колебаний, а не время такого затухания. Полное время затухания определяется отношением Т/б.
50)Действие периодической силы на затухающий гармонический осциллятор. Резонанс.
Гармонический осциллятор — система, которая при смещении из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x:
,
где k — коэффициент
жёсткости системы.
Если F — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором.
Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором.
Резонанс — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы.