Задача 55.

Дано уравнение эллипса .

Найти:

1. длины его полуосей;

2. координаты фокусов;

3. эксцентриситет эллипса;

4. уравнения директрис и расстояния между ними;

5. точки эллипса, расстояние от которых до левого фокуса равно 12.

Решение:

Запишем уравнение эллипса в каноническом виде: .

Отсюда . Используя соотношение, находим. Следовательно,.

По формуле найдем.

Уравнения директрис имеют вид, расстояние между ними.

По формуле находим абсциссу точек, расстояние от которых до точкиравно 12:

. Подставляя значениеxв уравнение эллипса, найдем ординаты этих точек:.

Таким образом, условию задачи удовлетворяет точка A(7;0).

Задача 56.

Составить уравнение эллипса, проходящего через точки .

Решение:

Уравнение эллипса ищем в виде .

Так как эллипс проходит через точки , то их координаты удовлетворяют уравнению эллипса:. Умножая второе равенство на (-4) и складывая с первым, находим.

Подставляя найденное значение в первое уравнение, найдем. Таким образом, искомое уравнение.

Задача 57.

Как расположены на плоскости точки, координаты которых удовлетворяют условиям:

;.

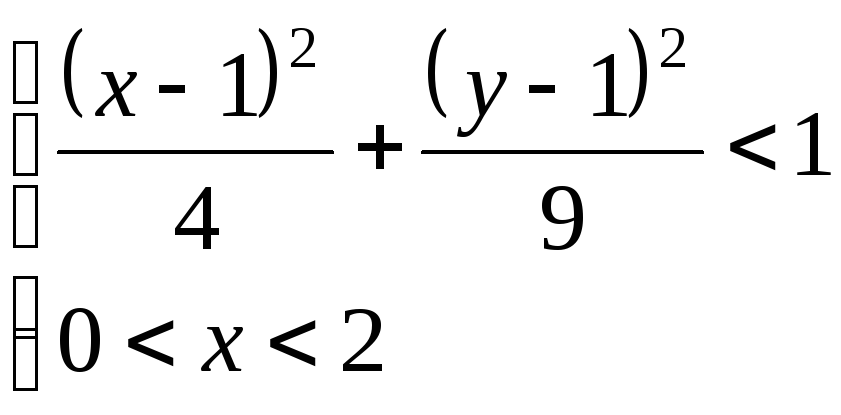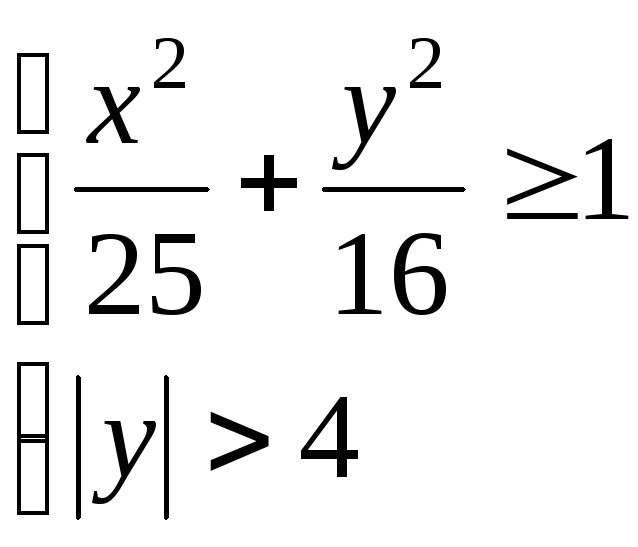Гипербола

Гиперболойназывается линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точекиесть величина постоянная (не равная нулю и меньшая, чем расстояние между точкамии).

Точки иназываютсяфокусамигиперболы. Пусть по-прежнему расстояние между фокусами равно. Модуль расстояний от точек гиперболы до фокусовиобозначим через. По условию,.

,

где ‑ координаты произвольной точки гиперболы,

.

Уравнение называетсяканоническим уравнениемгиперболы.

У гиперболы две асимптоты.

Эксцентриситетомгиперболы называется число. Для любой гиперболы.

Фокальными радиусами точки гиперболыназываются отрезки прямых, соединяющие эту точку с фокусамии. Их длиныизадаются формулами:

• Для правой ветви ,

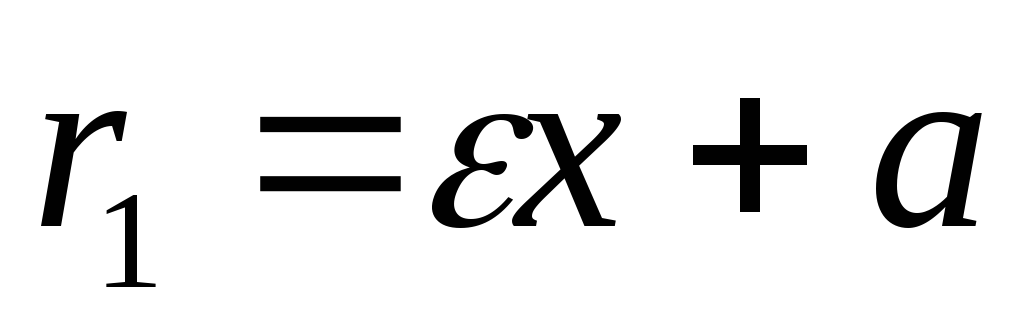• Для левой ветви .

Прямые называются директрисами гиперболы. Как и в случае эллипса, точки гиперболы характеризуются соотношением.

Задача 58.

Найти расстояние между фокусами и эксцентриситет гиперболы .

Ответ: .

Задача 59.

Написать каноническое уравнение гиперболы, если (). Определить эксцентриситет гиперболы.

Ответ: .

Задача 60.

Написать каноническое уравнение гиперболы, симметричной относительно осей координат, если она проходит через точку , а эксцентриситет равен.

Ответ: .

Задача 61.

Найти уравнения гиперболы, вершины которой находятся в фокусах, а фокусы в вершинах эллипса .

Ответ: .

Задача 62.

Определить геометрическое место точек , расстояния от которых до прямойвдвое меньше, чем до точки.

Ответ: .

Задача 63.

Составить уравнение гиперболы симметричной относительно системы координат, если она проходит через точки ,.

Ответ: .

Задача 64.

Составить уравнение гиперболы, если ее асимптоты заданы уравнением , и гипербола проходит через точку.

Ответ: .

Задача 65.

Как расположены на плоскости точки, координаты которых удовлетворяют условиям:

.

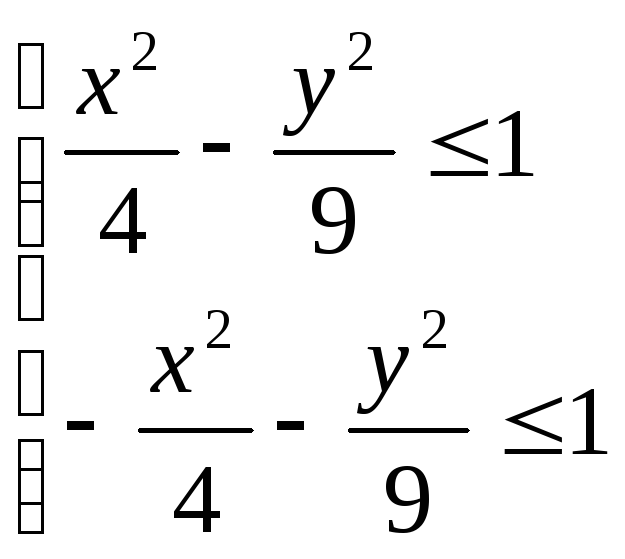Парабола

Параболойназывается линия, состоящая из всех точек плоскости, равноудаленных от данной точки(фокуса) и данной прямой(директрисы).

Для вывода канонического уравнения параболы ось проводят через фокусперпендикулярно директрисев направлении от директрисы к фокусу; начало координат берут в середине отрезка между фокусоми точкойпересечения осис директрисой. Если обозначить черезрасстояние фокуса от директрисы, тои уравнение директрисы будет иметь вид.

В выбранной системе координат уравнение параболы имеет вид: . Это уравнение называетсяканоническим уравнением параболы.