10.2. Непрямі показники якості

10.2.1. Частотні показники

Частотні показники визначають по частотних характеристиках замкнутого й розімкнутого контуру системи.

АЧХ замкнутої системи.

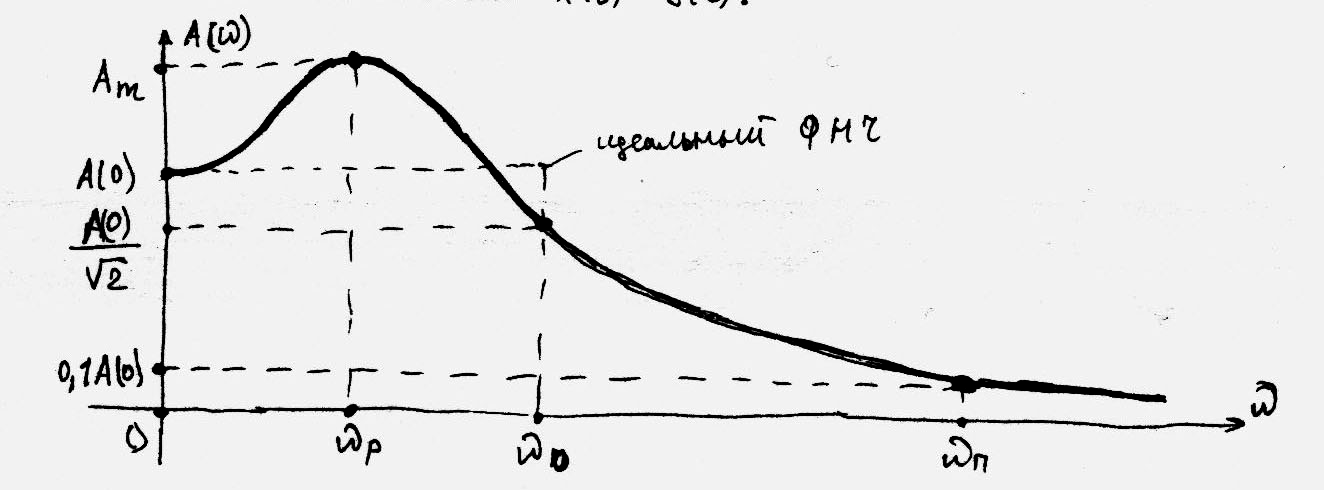
Частотний показник коливальності М: це відношення максимуму АЧХА_М до початкового значення АЧХ А(0).

Чим більше , тим сильніше коливальність системи (більше перерегулювання ), і як наслідок більше тривалість перехідного процесу t_п. Якість системи вважається задовільною, якщо показник М = 1,1...1…1,5

Непрямими частотними показниками швидкодії системи є характерні частоти.

• резонансна частота ω_р – відповідає піку АЧХ, близька до частоти коливань у перехідному процесі;

• смуга пропущення системи – це інтервал частот від ω=0 до ω₀, при якій виконується умова . Смуга пропущення не повинна бути занадто широкою, інакше система буде відтворювати високочастотні перешкоди. У той же час, чим менше смуга пропущення системи, тим більше інерційна система (більший час перехідного процесу).

АФЧХ (ЛЧХ) розімкнутої системи

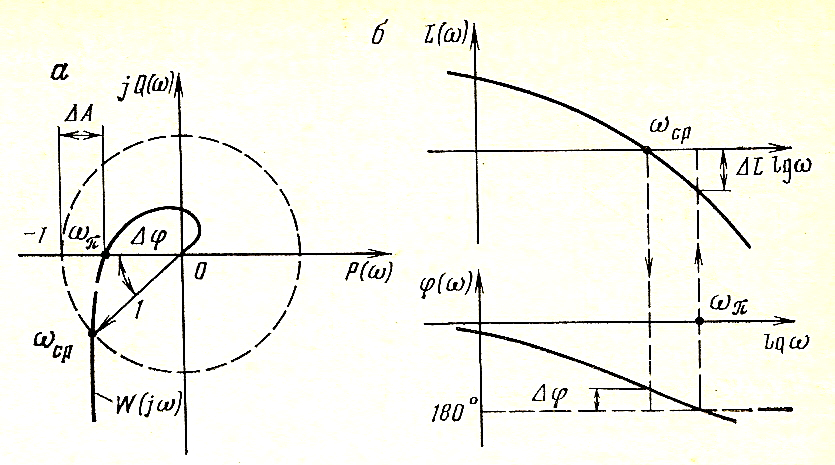
• запас стійкості по амплітуді

• запас стійкості по фазі

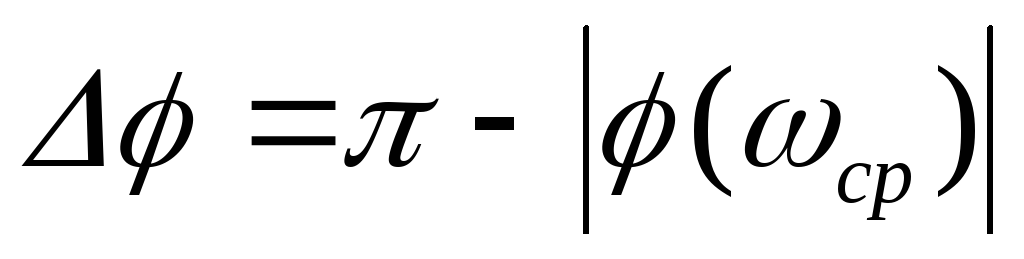
Показники якості ∆А й ∆φ разом характеризують далекість кривій W(jw) від критичної точки (-1; j0).

При проектуванні систем звичайно задаються запасом стійкості по амплітуді ∆А ≥0,5÷0,6 і по фазі ∆φ≥30÷60^о.

Варіанти	0 %	10..30 %	50..70 %
Застосовність	рідко	часто	уникають
Запас по фазі
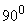
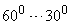
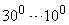
Число коливань	0	1, 2	3, 4,...

При рішенні задач синтезу САУ широке поширення одержали логарифмічні частотні характеристики. У цьому випадку запас стійкості по амплітуді визначається з вираження ∆L ≥ 6-8 дБ

Швидкодію системи можна приблизно оцінити по частоті зрізу ω_ср ЛАЧХ розімкнутої системи:

Необхідність прийняття запасів стійкості пов'язана з:

• зміною параметрів ОУ в процесі експлуатації (зношування, старіння...);

• лінеаризацією характеристик ОУ;

• погрішностями, що виникають при експериментальних дослідженнях характеристик ОУ.

ВЧХ замкнутої системи.

Якщо на лінійну систему діє гармонійний сигнал, то й стале значення вихідної величини буде гармонійним:

де - зображення вихідної величини y(t) за Фур'є;

- зображення вхідної величини x(t) за Фур'є;

- АФЧХ замкнутої системи.

При впливі на систему одиничної східчастої функції x(t)=1(t) вихідна величина, що є перехідною характеристикою системи h(t), визначається через дійсну частотну або мниму частотну характеристику замкнутої системи

(1)

(2)

Розглянемо основні властивості дійсних частотних характеристик і відповідних їм перехідних процесів. З (1) випливають основні властивості й h(t). Приведемо їх без доказів.

1. Властивість лінійності: якщо дійсну частотну характеристику можна представити сумою

,

те й перехідний процес h(t) може бути представлений сумою складових

, .

2. Відповідність масштабів по осі ординат для й h(t). Якщо помножити на постійний множник а, то відповідні значення h(t) теж множаться на цей множник а.

3. Початкове значення ДЧХ дорівнює кінцевому значенню перехідної характеристики

.

Початкове значення мнимої частотної характеристики .

4. Кінцеве значення ДЧХ дорівнює початковому значенню оригіналу перехідної характеристики

.

5. Відповідність масштабів по осі абсцис для та h(t). Якщо аргумент у відповідному виразі частотної характеристики помножити на постійне число (рис.), то аргумент у відповідному виразі перехідного процесу буде ділитися на це число.

Становлять інтерес розриви безперервності й піки у ДЧХ.

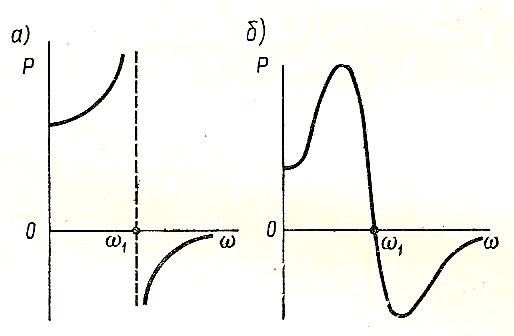
Припустимо, що при ДЧХ має розрив безперервності , при цьому характеристичне рівняння системи буде мати мнимий корінь тобто в системі встановлюються незгасаючі гармонічні коливання, якщо інші корені – ліві.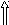

Характеристика для цього випадку показана на рис. а.

Високий і гострий пік частотної характеристики, за яким переходить через нуль, при частоті, близької до , відповідає повільно загасаючим коливанням (рис.б).

6. Щоб перехідна характеристика системи мала перерегулювання, яке не перевищує 18% (), ДЧХ повинна бути позитивною не зростаючою функцією частоти (рис. г), тобто.

в) г) д)

7. Умови монотонного протікання перехідного процесу. Щоб перехідний процес мав монотонний характер, досить, щоб відповідна йому ДЧХ була позитивною, безперервною функцією частоти з негативної, убутної по абсолютній величині похідній (рис. д), тобто (ВЧХ має ввігнутий вигляд).

8. Визначення найбільшого значення перерегулювання перехідного процесу по максимуму речовинної частотної характеристики (рис. в) ,

де - максимальне значення ;

- початкове значення ().

9. Тривалість перехідного процесу оцінюється приблизно по величині інтервалу істотних частот (частоті позитивності )

- для ДЧХ без вираженого максимуму

- для ДЧХ, що має максимум .