22.2. Передаточная функция формирующего звена

В модели линейной системы с амплитудно-импульсной модуляцией формирующее звено преобразует последовательность δ-функций в последовательность прямоугольных импульсов, т.е. прямоугольный импульс является реакцией формирующего элемента на воздействие в виде δ-функций. Таким образом, реакция формирующего звена на δ-функцию представляет собой весовую характеристику w_ф(t). Как известно, изображение по Лапласу весовой функции есть передаточная функция.

Определим передаточную функцию формирующего звена. Для этого представим прямоугольный импульс – весовую функцию формирующего звена в виде, как показано на рис.22.2.

Амплитуду прямоугольного импульса примем равной единице.

Изображение по Лапласу весовой функции w_ф(t):

.

Данное выражение представляет собой передаточную функцию формирующего звена.

τ=γT

T

w_ф(t)

t

t

k(t)

t

k(t-γT)

Рисунок 22.2. Представление прямоугольного импульса в виде двух скачкообразных функций

Если амплитуда прямоугольного импульса отлична от единицы и равна k_И, то передаточная функция формирующего элемента примет вид:

.

Аналогично определяется передаточная функция формирующего элемента, имеющего на выходе импульсы другой формы.

Если , то передаточная функция формирующего элемента определяется выражением:

.

Формирующий элемент с такой передаточной функцией называется фиксатором (экстраполятором) нулевого порядка. Такие фиксаторы получили наибольшее распространение в практике применения цифровых управляющих машин. Подавляющее большинство реальных восстанавливающих устройств описываются именно моделью фиксатора нулевого порядка. Это наиболее простой экстраполятор, легко реализуемый с помощью стандартной аппаратуры (ЦАП).

22.3. Математическое описание идеального импульсного элемента

Идеальный импульсный элемент представляет собой модулятор. Известно, что выходной сигнал модулятора равен произведению сигнала несущейна модулирующий сигнал.

Модулирующий сигнал есть последовательность- функций:

.

С учетом последовательности -функций выражение для выходного сигнала идеального импульсного элемента имеет вид:

.

Определим изображение по Лапласу функции . Для этого произведем некоторые преобразования.

;

.

Поскольку величина в течение периодаТ постоянна, то можно вынести за знак преобразованияD

.

Таким образом, изображение по Лапласу сигнала модулированного идеальным импульсным элементом по существу является дискретным изображением по Лапласу решетчатой функции соответствующей непрерывной функции.

Последнее выражение легко представить в виде z-изображения, применив подстановку :

.

Последовательность импульсов можно представить рядом Фурье

,

где - частота импульсов;

r – номер гармоники.

С учетом последнего выражения, сигнал можно записать в виде:

Применив к полученному выражению преобразование Лапласа и, учитывая теорему смещения, получим

Полученное соотношение устанавливает аналитическую связь между обычным и дискретным преобразованиями Лапласа и получило в литературе название прямого D-преобразования.

Перейдем далее к преобразованию Фурье сигнала .

Преобразование Фурье для k-го члена запишется в виде:

а для всего выражения

.

Последнее выражение показывает, что частотный спектр решетчатой функции представляет собой сумму частотных спектров модулирующего сигнала, смещенных по оси частот на величины.

Частотный спектр решетчатой функции показан на рис. 22.3.

Рисунок 22.3. Частотный спектр решетчатой функции

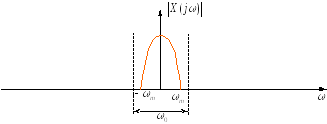
Рисунок 22.4. Частотный спектр непрерывного сигнала

Модуляция непрерывным сигналом последовательности-функцийприводит к появлению боковых (дополнительных) полос спектров, идентичных частотному спектру непрерывной функции, около частот, кратных частоте следования импульсов. Реально существуют спектры сигнала, расположенные справа от оси ординат.

Восстановление непрерывной функции, т.е. полезного сигнала может быть произведено по одной из полос спектра. Выделение полезной информации производится фильтрами низких частот, которые отфильтровывают боковые полосы модулированного сигнала. Обычно роль фильтров выполняют сами непрерывные инерционные элементы системы.

Для того чтобы выделить полезную информацию без искажений из модулированного сигнала, необходимо чтобы основной и дополнительные спектры не перекрывали друг друга (рис.22.4, рис.22.5).

Это условие можно сформулировать в виде теоремы, которая носит название теоремы В.А. Котельникова.

Чтобы исходная непрерывная функция была восстановлена без потери информации из модулированного сигнала, необходимо, чтобы частота следования импульсов была не менее чем в 2 раза выше наивысшей частотыв спектре полезного сигнала.

или

Если непрерывный сигнал обладает спектром, ограниченным частотой , то его квантование по времени с частотойне приводит к потере информации, т.е. сигнал однозначно и полностью представляется своими дискретными значениями, взятыми через интервал квантования.

Рисунок 22.5. Частотный спектр дискретного процесса

Теорема Котельникова-Шеннона

Непрерывный сигнал, преобразование Фурье которого равно нулю вне интервала (,),однозначно представляется своими значения в равноотстоящих точках, если частота квантования больше .Непрерывный сигнал может быть получен из дискретного по формуле