21. Математический аппарат исследования дискретных систем

21.1. Решетчатые функции и разностные уравнения.

Величины, описывающие поведение автоматических систем, представляют собой функции времени. Математическое исследование дискретных систем существенно упрощается в том случае, когда все величины рассматриваются в дискретные равноотстоящие моменты времени.

Решетчатая функция времени , или в сокращенной записи - это математическая функция, значения которой определены в дискретные равноотстоящие друг от друга моменты времени ,

где n - целое положительное число 0, 1, 2 ...,

Т - период дискретности.

То есть решетчатая функция представляет собой числовую последовательность:

, ,,, …,

На рис. 21.1 представлена разомкнутая цепь линейной дискретной системы с идеальным импульсным элементом (идеальным ключом), имеющим период замыкания T.

Под идеальным импульсным элементом будем понимать ключ, который замыкается на бесконечно малое время и в момент, когда ключ замкнут, его сопротивление равно нулю, а в разомкнутом состоянии его сопротивление равно бесконечности.

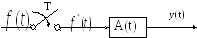
Рисунок 21.1 – Разомкнутая дискретная система с идеальным импульсным элементом

Если на вход такой цепи подать непрерывный сигнал (рис.21.2), то на выходе идеального импульсного элемента будет получен дискретный сигнал – решетчатая функция(рис.20.2).

Рисунок 21.2. Разомкнутая дискретная система с идеальным импульсным элементом

Если период дискретности T задан, то решетчатая функция однозначно формируется из исходной непрерывной. Обратная задача - формирование непрерывной функции из решетчатой - не может быть решена однозначно без дополнительных сведений о поведении функции в интервале между точками, так как функции, заданной в дискретные моменты времени, может соответствовать бесконечное множество непрерывных функций. Непрерывные функции, проходящие через дискреты заданной решетчатой функции, называют огибающими. Их бесконечно много (рис.21.3).

Рисунок 21.3. Восстановление непрерывной функции по решетчатой.

Для суждения о характере поведения непрерывной функции в интервалах между дискретными моментами времени водится понятие смещенной решетчатой функции, которая представляет собой числовую последовательность:

, ,,, …,,

где - постоянное число, называемое смещением, выбираемое из интервала.

Для удобства записи вводят переменную – относительное время . В этом случае непрерывной функции в относительном временибудет соответствовать решетчатая функцияили смещенная решетчатая функция, обозначаемая сокращенно.

Аналогами производных и интегралов непрерывных функций для решетчатых функций являются конечные разности и конечные суммы.

Конечные разности решетчатых функций бывают двух видов: прямые (упреждающие) и обратные (отстающие).

Первой прямой конечной разностью функции называется решетчатая функция вида.

Первая обратная конечная разность .

Вторую прямую конечную разность определяют как разность двух первых разностей .

Вторая обратная конечная разность .

Разности произвольного порядка k определяются при помощи рекуррентных соотношений:

где k = 1, 2, 3, ........

Пример 21.1. Пусть , тогда:

первая разность - ;

вторая разность - ;

k-тая разность -

Аналогами интеграла непрерывной функции в пределах от 0 до t для решетчатой являются неполная сумма и полная сумма:

Разностные уравнения (уравнения в конечных разностях) связывают между собой решетчатые функции и их конечные разности:

Разностное уравнение может быть записано:

- непосредственно через конечные разности

;

- через решетчатую функцию

;

Общее решение однородного разностного уравнения при некратных корнях характеристического уравнения может быть записано следующим образом:

где z_i - корни характеристического уравнения

C_i - постоянные коэффициенты.

Для получения возможности исследования решений разностных уравнений в общем виде широко используются дискретное преобразование Лапласа, z-преобразование, -преобразование, а также частотные методы.