3.1.3. Матричный метод.

Пусть дана система n линейных уравнений с n неизвестными:

,

которую можно записать в матричной форме, как

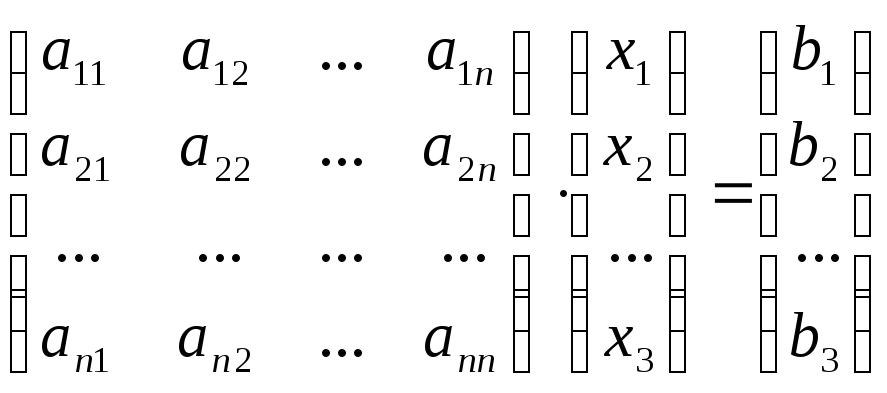, или ,

где

А=, х =, b =.

Предположим, что . В этом случае матрица имеет обратную . Умножим слева обе части системы на , и, выполнив преобразования,

получим:

т.е. .

Данное соотношение и представляет суть матричного метода.

Замечание. Матричный метод, как и правило Крамера, применим, если .

Пример 4. Решить систему матричным методом .

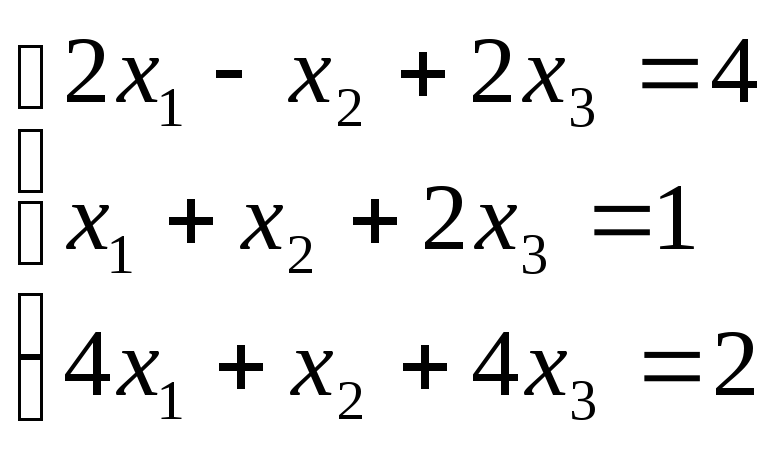Решение.

Имеем

, ,.

Таким образом существует. Найдём алгебраические дополнения:

Получим:

.

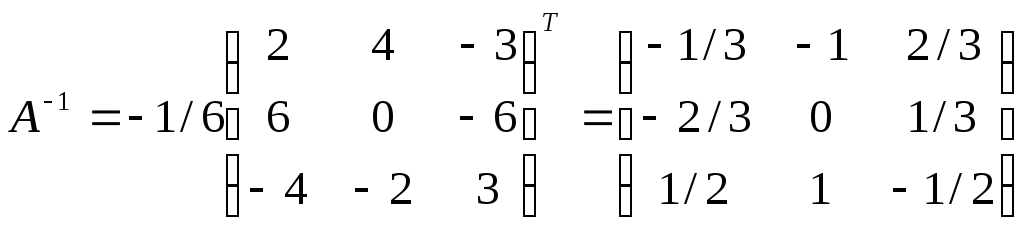Следовательно,

Т.е. _, ,.

Выполним проверку.

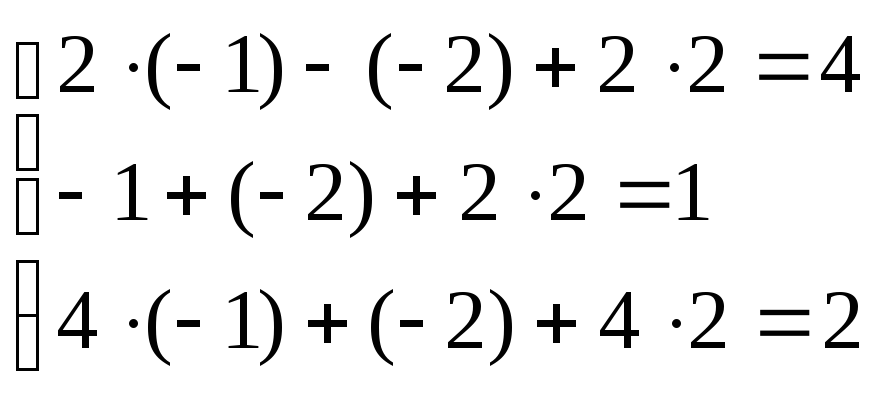
Решение найдено верно.

Ответ. (-1;-2;2).

3.2. Решение типовых примеров

1. Решить систему линейных алгебраических уравнений двумя способами: матричным методом и по правилу Крамера. Результаты сравнить.

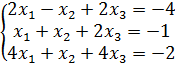
Решение.

Правило Крамера.

Найдем главный определитель системы по правилу треугольников. Имеем

.

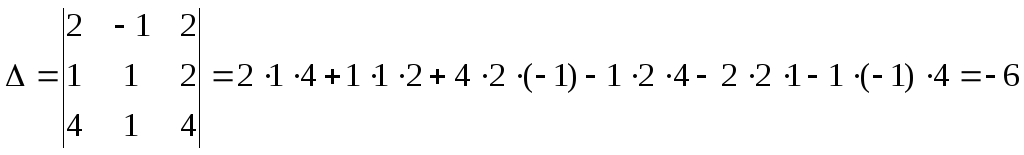Определим вспомогательные определители.

,

,

.

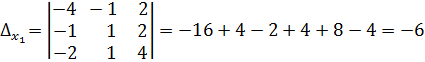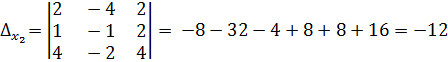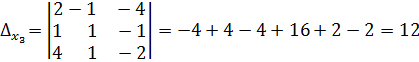Найдем значения переменных. Имеем

.

Матричный метод.

Таким образом существует. Найдём алгебраические дополнения:

,,,

,,,

,,

Имеем:

.

Следовательно,

.

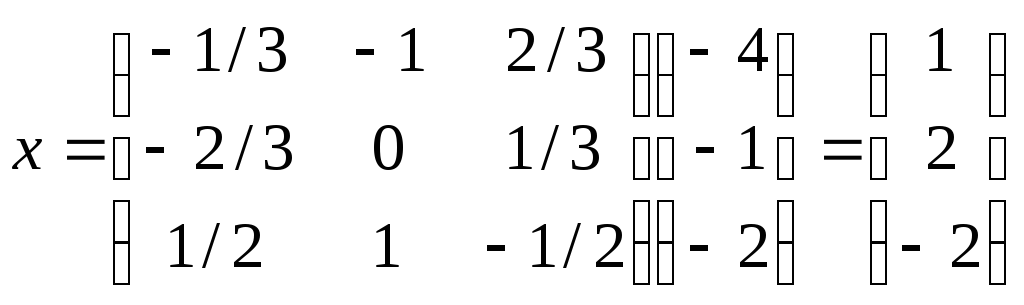Т.е.

Решив систему двумя способами, мы пришли к одному и тому же ответу (1;2;-2), значит, система решена правильно.

Ответ. (1;2;-2).

2. Решить систему линейных алгебраических уравнений методом Гаусса.

Решение.

Ход решения аналогичен примерам 1,2,3.

Приводим составленную таблицу к ступенчатому виду: умножаем первую строку на (-3), прибавляем к ней вторую, затем умножаем первую строку на (-4) и прибавляем к ней третью; Втору строку умножим на (-21), а третью на (10), результаты сложим. Имеем

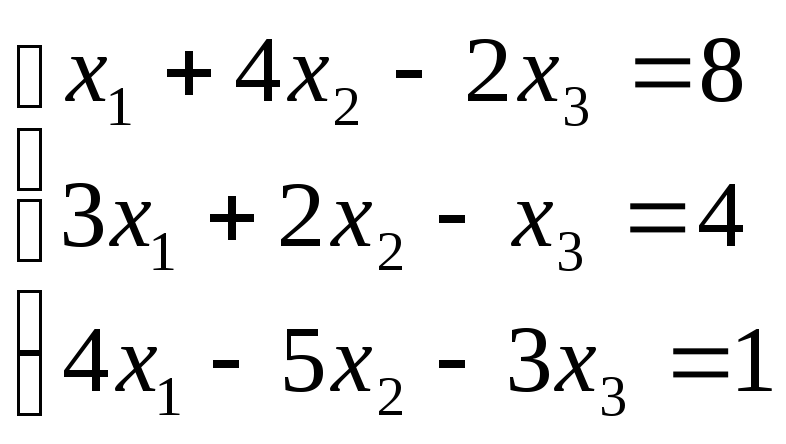
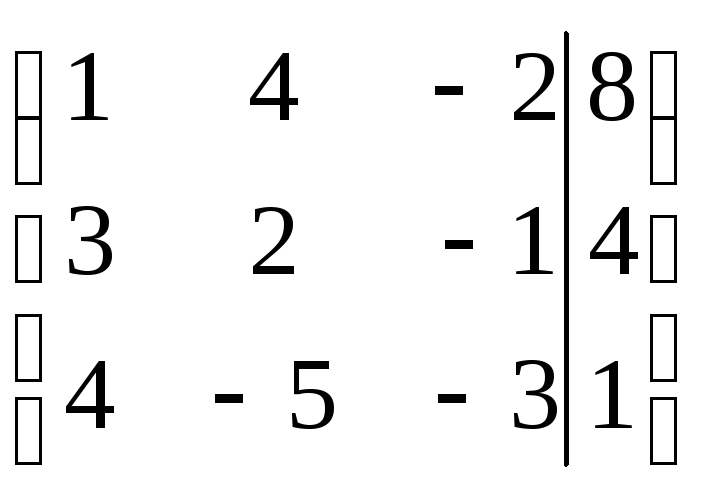
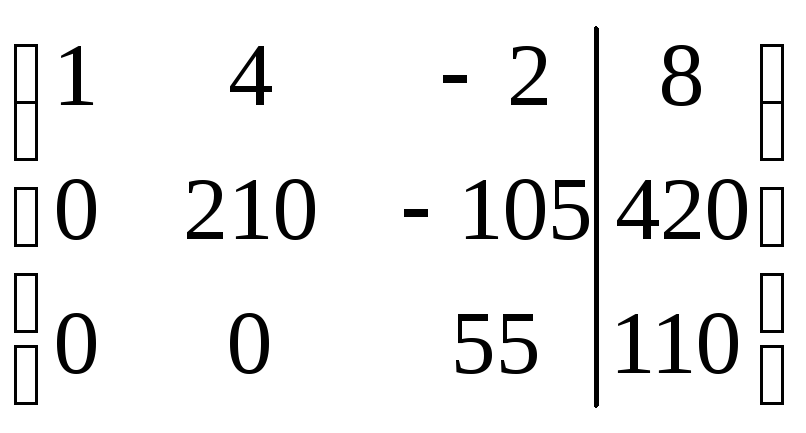
В результате получим следующую систему:

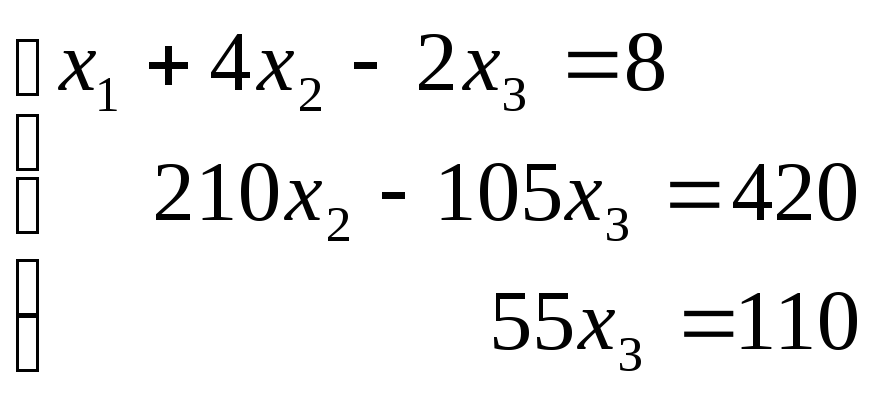
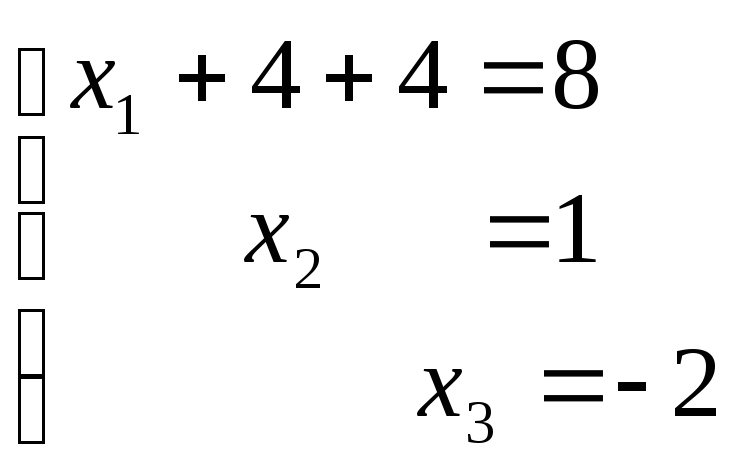
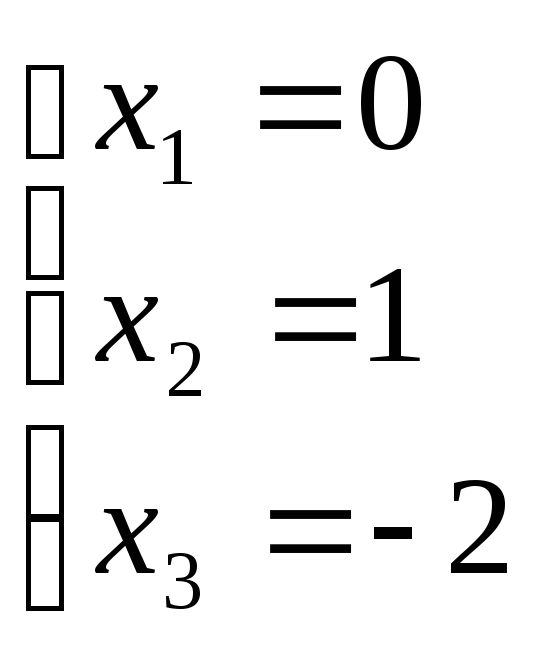
Выполним проверку

Решено верно.

Ответ. (0;1;-2).

3. При каких a и b система имеет

а) единственное решение;

б) не имеет решения;

в) бесчисленное множество решений.

Решение.

Найдём главный определитель системы по правилу Крамера. Если он будет отличен от нуля, тогда система будет иметь лишь одно решение.

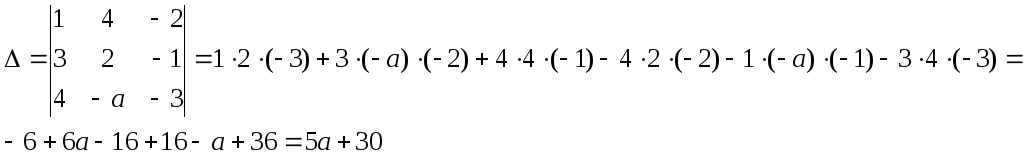
Главный определитель зависит от а. Он обращается в ноль при а=-6.

Если , тои система имеет только одно решение при любом.

Если , то получим следующую систему линейных уравнений 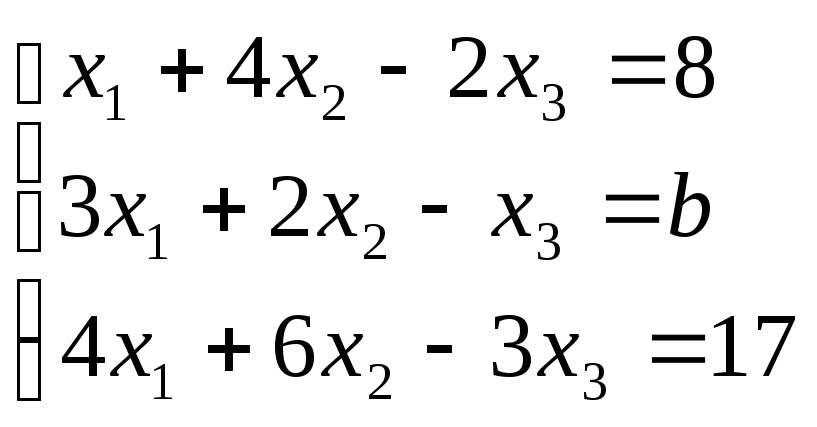, которой соответствует расширенная матрица :

Умножим первую строку на (-3) и сложим со второй, первую строку умножим на (-4) и сложим с третьей.

Заметим, что две последних строки матрицы имеют одинаковую левую часть. Поэтому, чтобы система была совместна необходимо, чтобы правые части также совпадали. При этом возможны следующие варианты.

Если =25, то два последних уравнения одинаковы. Опускаем одно из них, в результате чего исходная система трех уравнений сводится к системе двух уравнений, но с тремя неизвестными.

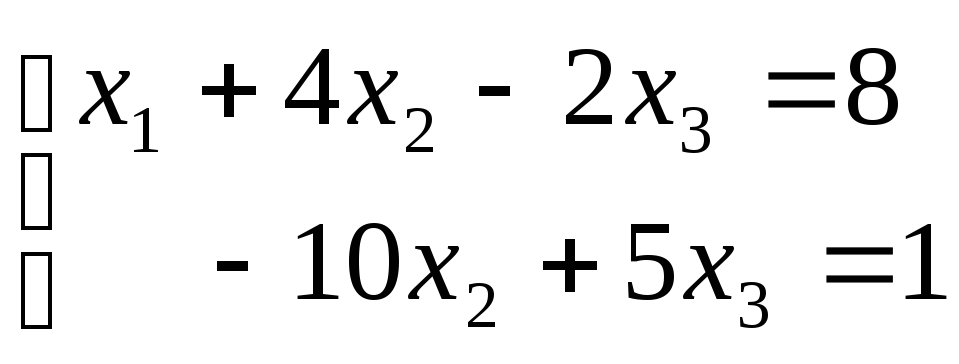
Эта система имеет бесконечное количество решений.

Если же , то система несовместна.

Ответ: Если , то система имеет единственное решение.

Если - система решений не имеет.

Если - система имеет бесконечно много решений.

4. Составить систему трёх линейных уравнений с тремя неизвестными, имеющую решение (8;7;5). Имеет ли полученная система другие решения?

Решение.

Возьмем произвольные коэффициенты при неизвестных,,.и рассмотрим систему

.

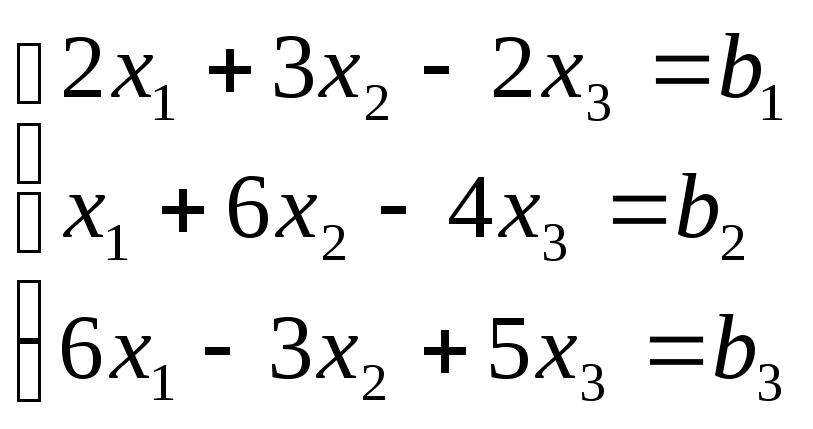Теперь, подставив решение (8;7;5), вычислим коэффициенты ,,

.

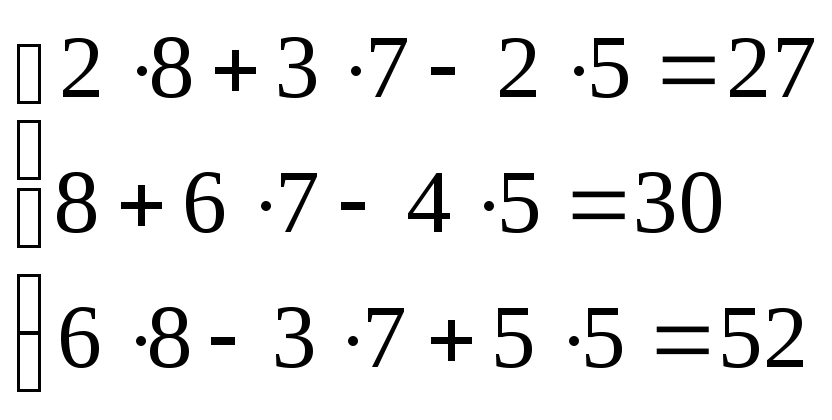Таким образом, мы получили систему, которая имеет решение (8;7;5)

.

Проверим эту систему на наличие других решений. С этой целью найдем ее главный определитель

.

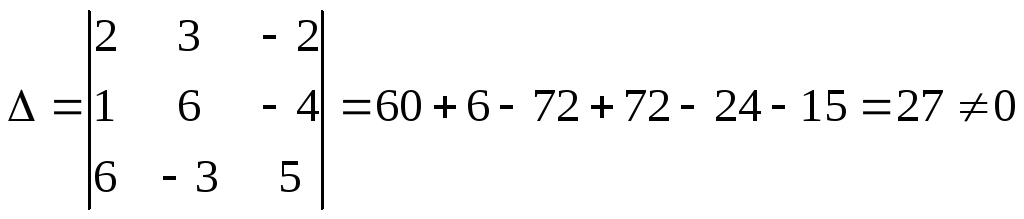Так как определитель составленной системы отличен от нуля, то эта система имеет единственное решение (8;7;5).

Замечание. Если бы , то составленная, таким образом ,система имела бы бесконечно много решений.

Ответ. .