
- •Методические указания для самостоятельной работы студентов по дисциплине «Элементы линейной алгебры и аналитической геометрии».
- •1. Определители, их свойства 5
- •1.2. Типовые примеры, задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •1.3 Варианты индивидуальных заданий
- •2. Матрицы
- •2.1. Определения, основные операции, свойства
- •2.2. Типовые примеры, задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •2.3. Варианты индивидуальных заданий
- •3. Решение систем линейных алгебраических уравнений
- •3.1. Основные методы
- •3.1.1. Правило Крамера.
- •3.1.2. Метод Гаусса.
- •3.1.3. Матричный метод.
- •3.2. Решение типовых примеров
- •3.3. Задачи для самостоятельного решения
- •3.4. Варианты индивидуальных заданий
- •4. Векторы
- •4.1. Понятие вектора, основные операции
- •4.1.1.Способы задания векторов
- •4.1.2. Линейные операции над векторами
- •4.1.2.1. Умножение вектора на число
- •4.1.2.2. Сложение (вычитание) векторов
- •4.1.3. Разложение вектора по базису
- •4.1.4. Скалярное произведение векторов
- •4.1.5. Векторное произведение векторов
- •4.1.6. Смешанное произведение векторов
- •4.2. Типовые примеры, методические указания
- •4.3. Варианты индивидуальных заданий
- •5. Плоскость в пространстве
- •5.1. Формы уравнения
- •5.1.1.Каноническое уравнение
- •5.1.2.Плоскость, проходящая через три заданные точки
- •5.1.3.Общее уравнение
- •5.2.Некоторые задачи, связанные с плоскостью
- •5.2.1.Угол между плоскостями
- •5.2.2.Расстояние от точки до плоскости
- •5.3.Типовые примеры, задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •5.4.Варианты индивидуальных заданий
- •6. Прямая в пространстве
- •6.2.2.Угол между прямой и плоскостью
- •6.2.3.Расстояние от точки до прямой
- •6.2.4.Расстояние между двумя скрещивающимися прямыми
- •6.3.Замечание
- •6.4. Примеры и задачи для самостоятельного решения
- •6. 5. Варианты индивидуальных заданий
- •7. Кривые второго порядка
- •7.1.Канонические формы уравнений
- •7.1.1. Эллипс
- •7.1.2. Окружность
- •7.1.3. Гипербола
- •7.1.4. Парабола
- •7.2. Общее уравнение кривых второго порядка, их классификация
- •7.3. Типовые примеры, задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •7.4. Варианты индивидуальных заданий
- •Список литературы
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ,
МОЛОДЁЖИ И СПОРТА УКРАИНЫ
ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Беловодский В.Н., Бабакина А.А.
Методические указания для самостоятельной работы студентов по дисциплине «Элементы линейной алгебры и аналитической геометрии».
(Для студентов заочной формы обучения
специальностей 6.05010101 и 6.05010105
«Информационные управляющие системы»,
«Компьютерный эколого-экономический мониторинг»,
«Программирование медиа-систем и компьютерный дизайн».)
Рассмотрено на заседании
кафедры КСМ
Протокол №2 от 16.09.11
Утверждено на заседании
учебно-издательского
Совета ДонНТУ
протокол № 6 от 06.10.11
Донецк -2011
УДК 512.8
Методические указания для самостоятельной работы студентов по дисциплине «Элементы линейной алгебры и аналитической геометрии».(Для студентов заочной формы обучения специальностей 6.05010101 и 6.05010105 «Информационные управляющие системы», «Компьютерный эколого-экономический мониторинг», «Программирование медиа-систем и компьютерный дизайн».) Сост.: Беловодский В.Н., Бабакина А.А.- Донецк, ДонНТУ, 2011.-105 стр.
Приведены краткие теоретические сведения, методические указания и задания к выполнению индивидуальных работ по курсу «Элементы линейной алгебры и аналитической геометрии» для студентов заочной формы обучения специальностей «Компьютерный экологический мониторинг», «Программирование и компьютерный дизайн» и «Информационные и управляющие системы». Изложены вопросы, связанные с основными понятиями линейной алгебры (определители, матрицы, системы линейных уравнений, векторы) и аналитической геометрии (прямая и плоскость в пространстве, кривые второго порядка). Каждый раздел содержит образцы решения типовых примеров, задачи для самостоятельного решения и наборы индивидуальных заданий.
Методическое пособие направлено на изложение теоретических основ курса линейной алгебры и аналитической геометрии и формирование практических навыков по решению типовых задач.
Рецензент: доцент кафедры КСМ к.ф.-м.н. Г.Т. Климко
Содержание
1. Определители, их свойства 5
1.1. Определения, правила вычисления 5
1.2. Типовые примеры, задачи для самостоятельного решения 8
1.3 Варианты индивидуальных заданий 10
2. Матрицы 13
2.1. Определения, основные операции, свойства 13
2.2. Типовые примеры, задачи для самостоятельного решения 16
2.3. Варианты индивидуальных заданий 22
3. Решение систем линейных алгебраических уравнений 24
3.1. Основные методы 24
3.1.1. Правило Крамера. 24
3.1.2. Метод Гаусса. 25
3.1.3. Матричный метод. 28
3.2. Решение типовых примеров 30
3.3. Задачи для самостоятельного решения 35
3.4. Варианты индивидуальных заданий 36
4. Векторы 39
4.1. Понятие вектора, основные операции 39
4.1.1.Способы задания векторов 39
4.1.2. Линейные операции над векторами 39
4.1.2.1. Умножение вектора на число 40
4.1.2.2. Сложение (вычитание) векторов 40
4.1.3. Разложение вектора по базису 40
4.1.4. Скалярное произведение векторов 41
4.1.5. Векторное произведение векторов 42
4.1.6. Смешанное произведение векторов 44
4.2. Типовые примеры, методические указания 46
4.3. Варианты индивидуальных заданий 52
5. Плоскость в пространстве 55
5.1. Формы уравнения 55
5.1.1.Каноническое уравнение 55
5.1.2.Плоскость, проходящая через три заданные точки 55
5.1.3.Общее уравнение 56
5.2.Некоторые задачи, связанные с плоскостью 57
5.2.1.Угол между плоскостями 57
5.2.2.Расстояние от точки до плоскости 58
5.3.Типовые примеры, задачи для самостоятельного решения 58
5.4.Варианты индивидуальных заданий 65
6. Прямая в пространстве 67
6.1.Формы уравнений 67
6.1.1.Канонические уравнения 67
6.1.2.Параметрические уравнения 67
6.1.3.Прямая, проходящая через две точки 68
6.1.4.Общие уравнения прямой 68
6.2.Некоторые основные задачи 68
6.2.2.Угол между прямой и плоскостью 70
6.2.3.Расстояние от точки до прямой 71
6.2.4.Расстояние между двумя скрещивающимися прямыми 71
6.3.Замечание 73
6.4. Примеры и задачи для самостоятельного решения 73
6. 5. Варианты индивидуальных заданий 82
7. Кривые второго порядка 85
7.1.Канонические формы уравнений 85
7.1.1. Эллипс 85
7.1.2. Окружность 87
7.1.3. Гипербола 88
7.1.4. Парабола 91
7.2. Общее уравнение кривых второго порядка, их классификация 93
7.3. Типовые примеры, задачи для самостоятельного решения 94
7.4. Варианты индивидуальных заданий 101
Список литературы 103
1. Определители, их свойства
1.1. Определения, правила вычисления
Понятие определителя было введено во второй половине XIX века в связи с разработкой основ теории решения линейных систем алгебраических уравнений. Под определителем понимается число, представленное в виде квадратной таблицы чисел, заключенной между вертикальными отрезками, которое вычисляется по определенным правилам.
Пусть дана некоторая
квадратная таблица чисел 2х2:
 .
.
Определителем
(детерминантом)
порядка 2
называется число![]() ,
которое вычисляется по следующему
правилу:
,
которое вычисляется по следующему
правилу:
![]() =
=
![]() =
=![]()
![]() -
-
![]()
![]() .
.
Определитель 3-го порядка для квадратной таблицы чисел 3х3 называется число, которое вычисляется по правилу:
![]()
 =
=![]()
![]()
![]() +
+![]()
![]()
![]() +
+![]()
![]()
![]() -
-
-![]()
![]()
![]() -
-![]()
![]()
![]() -
-![]()
![]()
![]() .
.
Это выражение хорошо запоминается с помощью специального мнемонического правила называемого, правилом треугольников. Схематически его можно представить так:
« + » « - »

 ,
,
где слева указаны произведения элементов, входящих в выражение (3) со знаком «+», справа,- со знаком «-» .
Для вычисления определителей более высоких порядков используется правило, основанное на понятии алгебраического дополнения.
Рассмотрим элемент
![]() .
Удалим из определителя i-ю
строку и j-ый
столбец. Оставшиеся элементы образуют
определитель порядка (n-1).
Он называется
минором
элемента
.
Удалим из определителя i-ю
строку и j-ый
столбец. Оставшиеся элементы образуют
определитель порядка (n-1).
Он называется
минором
элемента
![]() и обозначается символом
и обозначается символом
![]() .
Тогда число
.
Тогда число
![]() =
=
![]()
![]()
![]()
![]() ,
,
называется
алгебраическим
дополнением элемента
![]() .
Справедливо утверждение: сумма
произведений элементов любой строки
(или столбца) на их алгебраические
дополнения равна определителю
.
Справедливо утверждение: сумма
произведений элементов любой строки
(или столбца) на их алгебраические
дополнения равна определителю
![]() .
Т.е.
.
Т.е.
![]() +
+![]() +…
+
+…
+![]() =
=
![]() +
+![]() +…
+
+…
+
![]() =…=
=…=
=![]() +
+![]() +…+
+…+
![]() =
=
![]() +
+![]() +…
+…![]() =…=
=…=![]() .
.
Данное правило удобно тем, что позволяет сводить вычисление одного определителя n-го порядка к вычислению n определителей порядка (n-1), понижая, тем самым, порядок оперируемых определителей.
Пример 1. Вычислить
определитель
 .
.
Решение:
Возьмём первую
строку. Для элемента 4 – алгебраическое
дополнение
![]()
 ,
для элемента 2 – алгебраическое дополнение
,
для элемента 2 – алгебраическое дополнение![]()
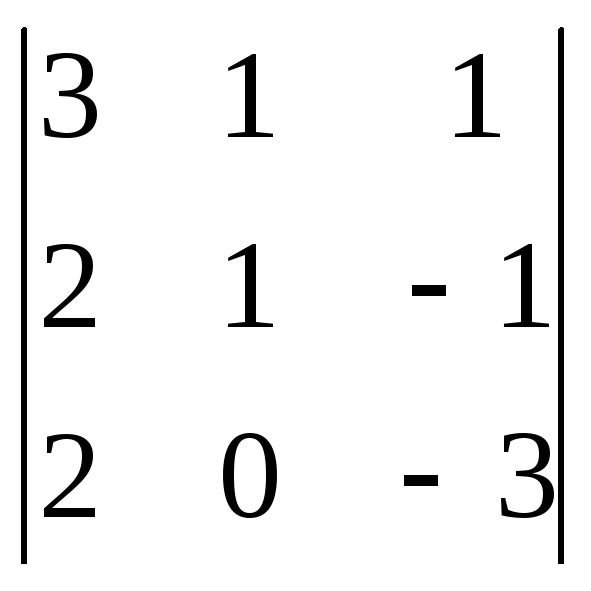 ,
для элемента 0 - алгебраическое дополнение
,
для элемента 0 - алгебраическое дополнение![]()
 ,
для элемента -2 - алгебраическое
дополнение
,
для элемента -2 - алгебраическое
дополнение![]()
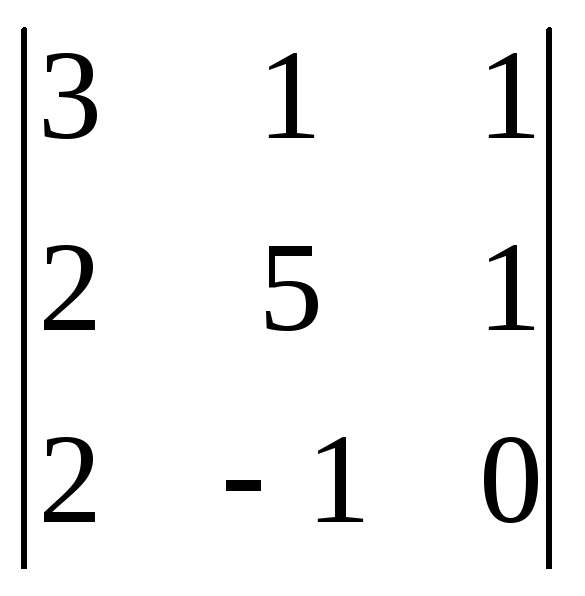 .
Таким образом,
.
Таким образом,
![]() 4
4![]()
 +2
+2![]()
 +0
+0![]()
 +(-2)
+(-2)![]()
 =
=
=4![]() 14+2
14+2![]() (-7)+0
(-7)+0![]() (-56)+(-2)
(-56)+(-2)![]() (-7)=56+14-0-14=56.
(-7)=56+14-0-14=56.
Ответ: 56.
Замечание. Если в строках таблицы встречаются нулевые элементы, то целесообразно стараться проводить разложение определителя по той его строке, в которой нулевых элементов больше.
В ряде случаев удается упростить вычисление определителя, предварительно преобразовав его, воспользовавшись свойствами:
При умножении всех элементов строки или столбца определителя на некоторое число её определитель также умножается на это число.
Определитель не изменится, если к одной строке поэлементно прибавить другую строку, умноженную на некоторое число.
При перестановке двух строк или столбцов знак определителя меняется на противоположный.
Два последних свойства определителя позволяют привести таблицу определителя к треугольному виду, тогда определитель с точностью до знака совпадёт с произведением диагональных элементов:
 и
и
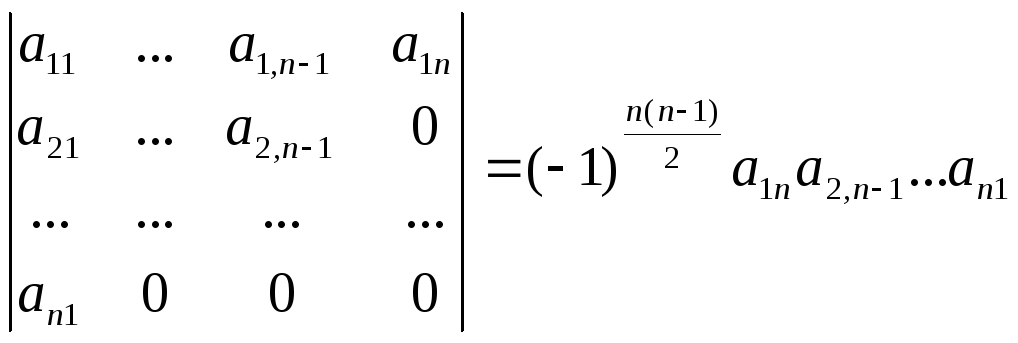
Пример 2.Вычислить
определитель
![]() =
=
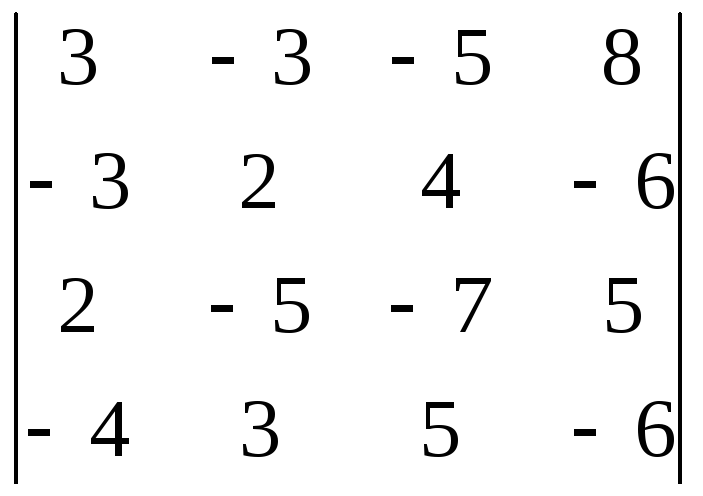 .
.
Решение:
Шаг 1.Прибавим ко второй строке первую, а к четвёртой – третью, умноженную на 2.
Шаг 2.Умножим третью строку на 3. Для того, чтобы значение определителя не изменилось, умножим полученный определитель на 1/3.
Шаг 3. Умножим первую строку на -2 и прибавим к ней третью. При этом, согласно второго свойства, значение определителя не изменится.
Шаг 4. Умножим вторую строку на -9 и прибавим ее к третьей, а вторую строку на -7 и прибавим к ней четвёртую.
Шаг 5. Умножим третью строку на -1 и прибавим к ней четвёртую.
Шаг 6. Воспользуемся формулой (4).
Имеем
 =
=
 =
=![]()
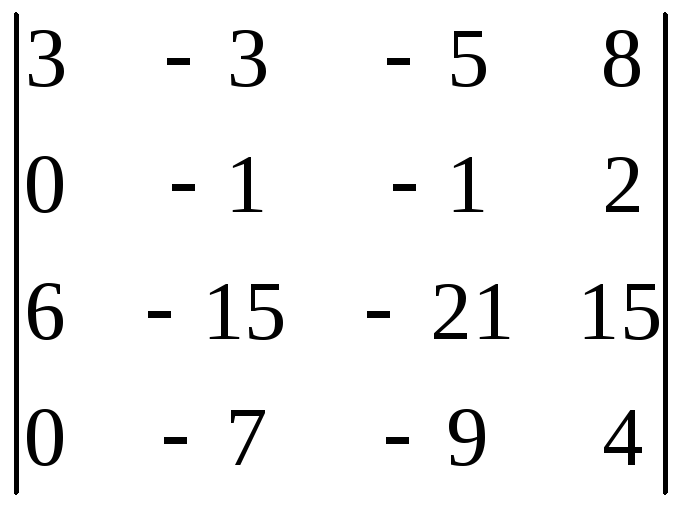 =
=
=
![]()
 =
=![]()
 =
=![]()
 =
=
=
![]()
![]() = 18 .
= 18 .
Ответ: 18.
