2.2. Типовые примеры, задачи для самостоятельного решения

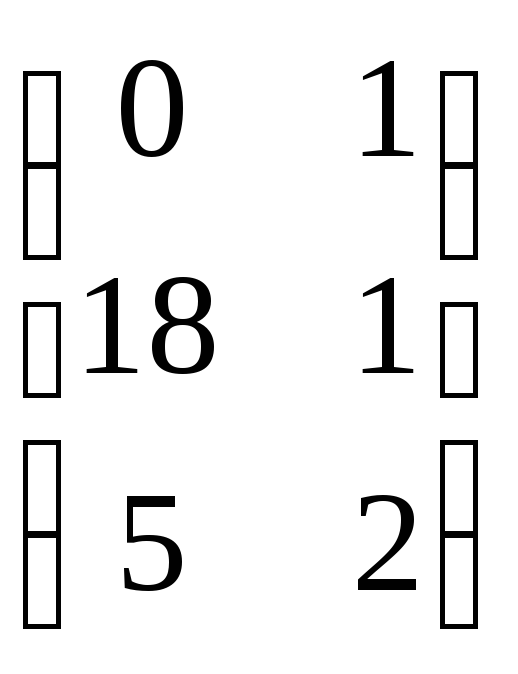
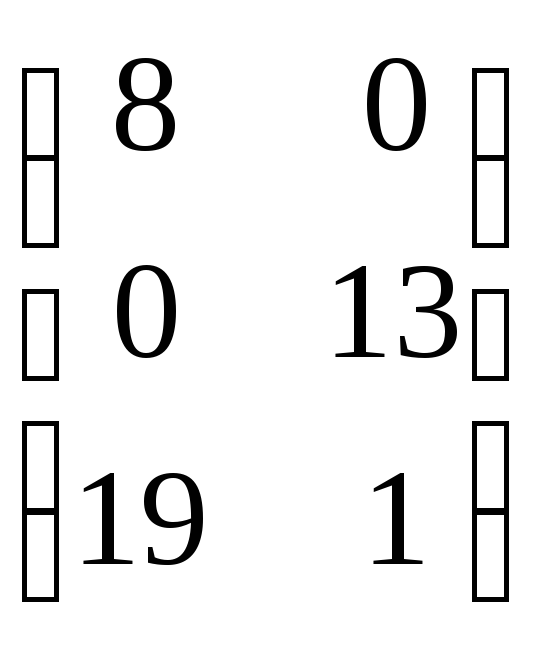
1. Даны матрицы А, В, С, D. Найти А+В, А-В, В-А, А², В³, СD.

; ;;.

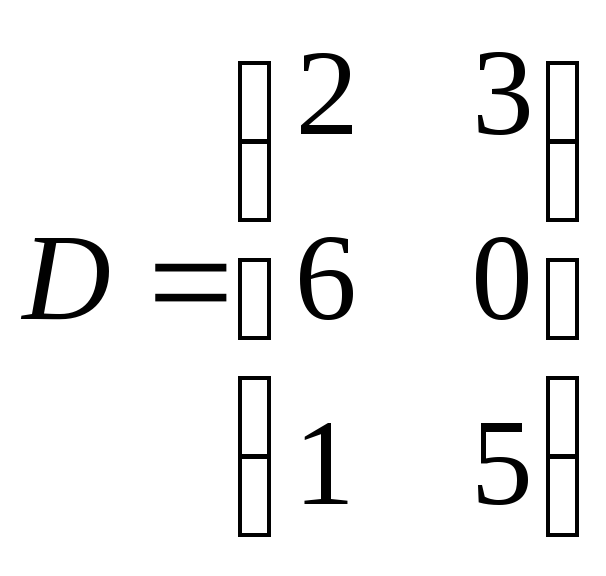Решение:

Согласно п.2.1, имеем

А+В==

А-В==

В-А=-=

А²⁼

В³=

СD==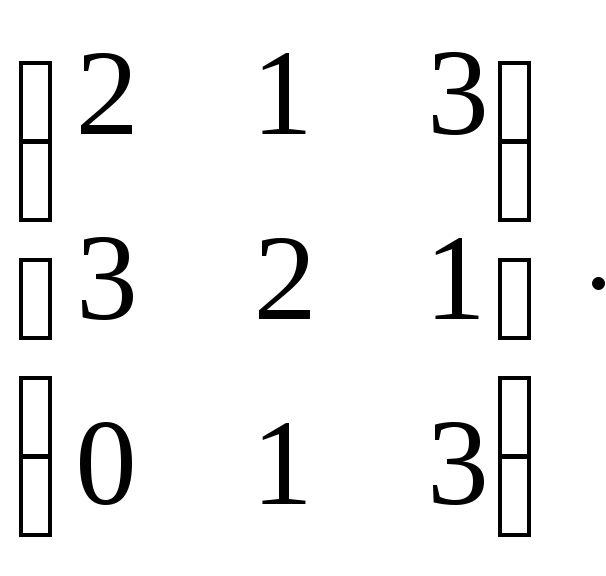

Ответ: А+В=;А-В=;В-А=;А²=;

В³=; СD=.

2. Найти обратные матрицы к матрицам А и С.

; .

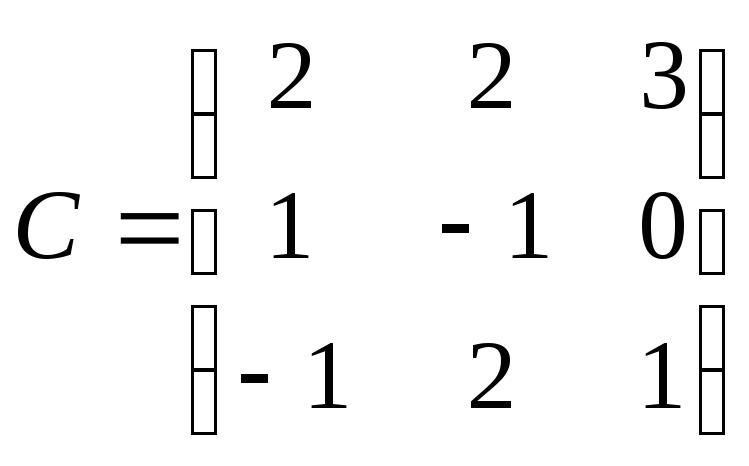Решение:

Для матрицы А

Шаг 1. Найдем определитель матрицы А.

Имеем

Шаг 2. Составим присоединенную матрицу .

Определим алгебраические дополнения:

Таким образом,

.

Шаг 3. Транспонируем полученную присоединённую матрицу

=

Шаг 4. Составим обратную матрицу:

,или.

Шаг 5. Проверим результат. Ограничимся вычислением

Найдём теперь обратную матрицу для матрицы С

Шаг 1. Найдем определитель матрицы С.

Имеем

Шаг 2. Составим присоединенную матрицу .

Определим алгебраические дополнения:

Таким образом,

.

Шаг 3. Транспонируем полученную присоединённую матрицу

=

Шаг 4. Составим обратную матрицу:

,или.

Шаг 5. Проверим результат. Ограничимся вычислением

Ответ: ; .

3. Решить матричное уравнение .

Решение.

Уравнение имеет вид . Для того, чтобы найти необходимо и левую и правую части уравнения умножить слева на А^-1: ,, .Здесь Е - единичная матрица, представленная ранее. Она обладает свойством .

В данном примере . Построим:

Составим присоединенную матрицу .

Найдем алгебраические дополнения:

.

Транспонируем :.

Найдём обратную матрицу=.

Теперь найдём Х:

.

Ответ: .

Замечание. Если уравнение имеет вид , то для того, чтобы найтинеобходимо и левую и правую части уравнения умножить уже справа на А^-1: ,, .

Такой способ решения матричных уравнений можно применять только в том случае, если матрица А^-1 существует ().

4. Найти все матрицы второго порядка, удовлетворяющие уравнению:

.

Решение.

Имеем

, .

Воспользуемся методом, который, как правило, можно использовать к решению матричных уравнений. Представим матрицу в виде

.

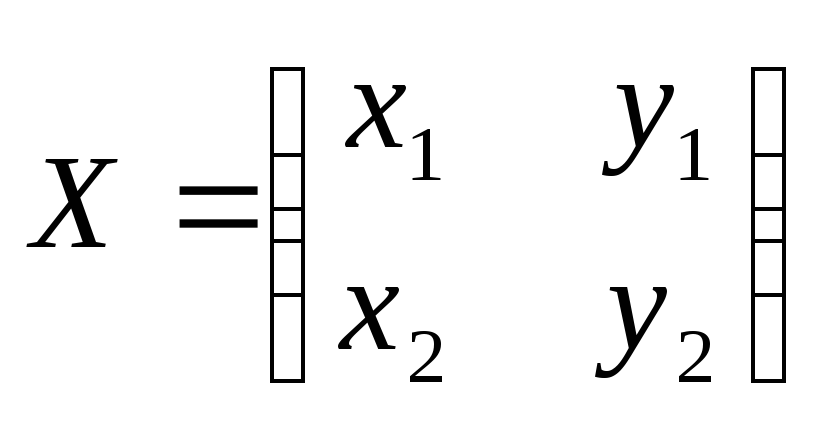Тогда исходное уравнение примет вид

,

или после перемножения,

.

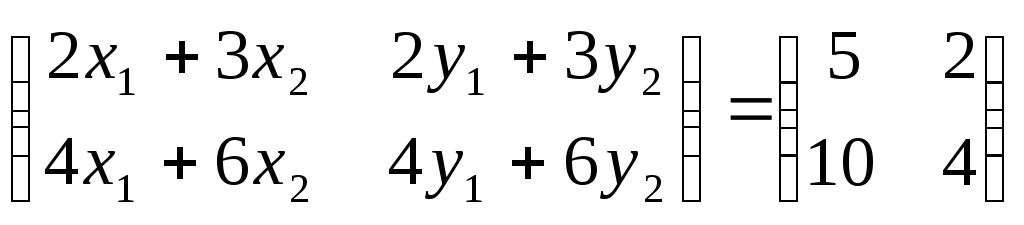Отсюда, сравнивая соответствующие элементы,

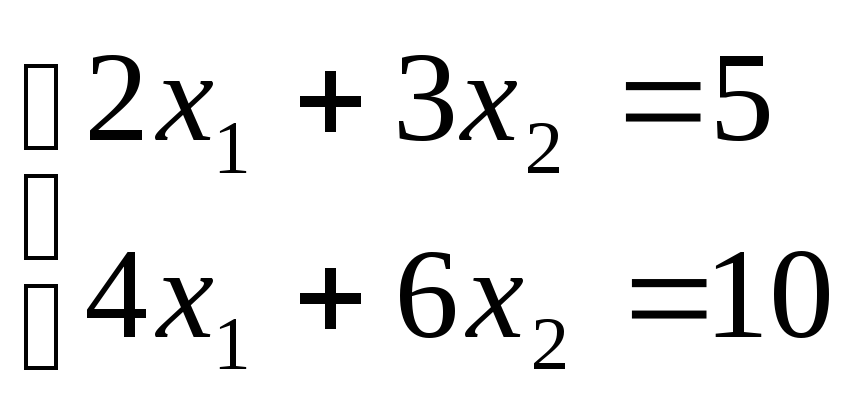и .

Обе системы имеют бесконечное количество решений. Отбросим в каждой из систем вторые уравнения и выразим одну переменную через другую

, ,

где - произвольные числа. Таким образом, окончательно, матрицаХ имеет вид:

,.

Ответ: ,.

Задачи для самостоятельного решения

1. Даны матрицы А, В, С. Вычислить А+В, А-В, А*В, А*С, А².

а) ;;;

б) ;;.

Ответ: : a)А+В=;А-В=;АВ=; AC=;А²=;

б) А+В=;А-В=;АВ=; AC=;А²=;

2. Найти произведение матриц .

Ответ:

3. Найти матрицу, обратную к . Используя формулуАА^-1=Е, проверить ответы.

Ответ: А^-1=

4. Решить матричные уравнения: а);

б) .

Ответ: а); б).

2.3. Варианты индивидуальных заданий

1. Даны матрицы А, В, С, D. Найти А+В, А-В, В-А, А², В³, СD.

2. Найти матрицы обратные к А и С.

3. Решить матричное уравнение.

Исходные данные:

	Матрицы				Уравнение
	А	В	С	D
Вариант 1
Вариант 2					=
Вариант 3					=
Вариант 4
Вариант 5
Вариант 6					=
Вариант 7
Вариант 8					=
Вариант 9
Вариант 10					=
Вариант 11
Вариант 12
Вариант 13
Вариант 14					=
Вариант 15					=