Нейросетевые технологии / АСУ Скобцов Искусственные нейронные сети лекции

1

НЕЙРОННЫЕ СЕТИ В КОМПЬЮТЕРНОЙ ИНЖЕНЕРИИ

Нейронные сети (НС) представляют новую и перспективную вычислительную технологию, дающую новые подходы к исследованию сложных и трудно формализуемых задач. Первоначально они были разработаны для решения задач распознавания образов. В настоящее время применяются в следующих областях: распознавание образов и изображений,

обработка зашумленных данных (фильтрация), сжатие данных,

классификация и кластеризация данных, ассоциативный поиск, решение оптимизационных задач, задачи диагностики, управление сложными процессами, моделирование сложных процессов, финансовая математика ,

задачи прогнозирования и многие другие.

Идея разработки интеллектуальных систем обработки информации по образу нервной системы возникла давно. В 1943 г. Маккалах и Питс создали упрощенную модель нервной клетки – искусственный нейрон. Параллельно с прогрессом в области нейроанатомии и нейрофизиологии были разработаны модели человеческого обучения. Далее в 50-60 годы XX века, группа исследователей, объединив эти два направления, создала первые искусственные нейросети и методы их обучения.

В последние годы нейросетевые технологии бурно развиваются поскольку: во-первых, в этой области сформировалась серьезная теоретическая база; во-вторых, достижения современной электроники позволяют практическую реализацию быстродействующих и недорогих нейрокомпьютеров, которые с успехом используются во многих сферах человеческой деятельности. За последние десять лет на русском языке опубликовано достаточно много литературы, часть которой представлена в приведенном списке литературы (в частности, [1-4]).

Отношение НС и компьютерной инженерии двоякое. С одной стороны,

нейрокомпьютеры являются подклассом параллельных компьютерных систем, которые постепенно вытесняют классические машины фон Неймана;

3

Таким образом, нейрон имеет много входов (дендритов) и один выход

(аксон). Соединение между нейронами реализуется в синапсах. Принятые синапсом сигналы подводятся к телу нейрона. Здесь они суммируются,

причем одни входы стремятся возбудить нейрон, другие воспрепятствовать возбуждению. Когда сумма возбуждающих сигналов в теле превышает некоторый порог, нейрон возбуждается, посылая по аксону сигнал возбуждения другим нейронам. У этой функциональной схемы есть много обобщений, но, тем не менее, большинство моделей искусственного нейрона моделируют только эти простейшие свойства.

Искусственным или формальным нейроном называется элементарный процессор, используемый в узлах нейронной сети. Математическую модель искусственного нейрона можно представить выражением

где у - выходной сигнал нейрона; f (s) - функция выходного блока нейрона; wi - синаптический коэффициент - вес i-го входа; xi - i-й входной сигнал; w0

- начальное возбуждение или смещение нейрона, i 1, n - номер входа нейрона и n - число входов. Выражению (1) может быть поставлена в соответствие структурная схема искусственного нейрона, представленная на рис.2. Как видно из рисунка, схема формального нейрона включает n входных блоков умножения на коэффициенты wi , один сумматор (часто называемый разными авторами адаптивным сумматором) и выходной блок функционального преобразования. Функция, которую реализует выходной блок, получила название функции активации (функции возбуждения или переходной функции). Коэффициенты wi называются синаптическими коэффициентами или коэффициентами межнейронной связи. Эти коэффициенты являются аналогами синапсов биологических нейронов. Если

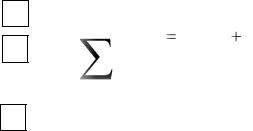
4

значение коэффициента wi отрицательное, то принято считать i-ю связь тормозящей, если положительное - возбуждающей.

Рис.2 Искусственный нейрон

В общем случае функционирование искусственного нейрона заключается в следующем (Рис.2). Перед началом работы на блок сумматора

подают сигнал начального смещения (начального возбуждения) w0 . На каждый i-й вход нейрона поступают сигналы xi либо от других нейронов,

либо с устройства ввода. Каждый i-й входной сигнал xi умножается на коэффициент межнейронной связи (синаптический коэффициент) wi . В блоке сумматора взвешенные входные сигналы и начальное возбуждение w0

алгебраически складываются. Результат суммирования (взвешенная сумма) s

подается на блок функционального преобразования f (s) . Итак, на выходе

первого каскада рис.2, как правило, реализуется скалярное произведение вектора синаптических коэффициентов W (параметры нейрона) и входного

различным для разных типов (или даже слоев) нейросетей. Основные типы используемых во втором каскаде активационных функций представлены ниже на рис.3

5

Рис.3 Типовые активационные функции

В настоящее время наиболее распространенными на практике являются следующие активационные функции :

Таким образом, искусственный нейрон можно рассматривать как процессор с ограниченной специальной системой команд (в нейросетевом базисе).

1.2. Основные типы архитектуры нейронных сетей

Нейросети представляют собой совокупность искусственных

нейронов, определенным образом соединенных между собой и с внешней

6

средой с помощью связей, определяемых весовыми коэффициентами wij.

Множество параллельно работающих процессоров обеспечивают высокое быстродействие НС.

В целом вид выполняемого сетью преобразования обусловлен не только характеристиками составляющих ее нейронов, но и особенностями архитектуры сети, а именно топологией межнейронных связей, способами обучения этой сети, наличием или отсутствием конкуренции между нейронами, направлением и способом управления и синхронизации,

способом передачи информации между нейронами.

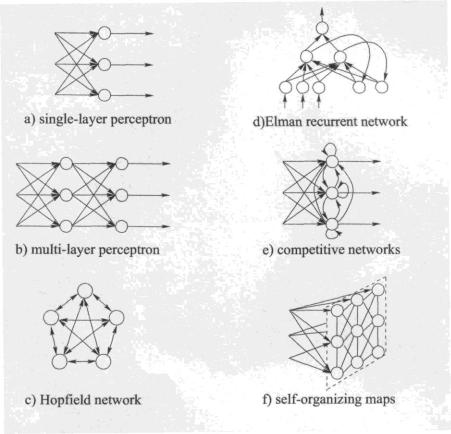
С точки зрения топологии можно выделить следующие основные типа НС, представленные на рис.4.

Рис.4 Основные типы топологий НС:

7

1)Сети с прямыми связями. Простейшими из них являются однослойные НС (однослойный перцептрон - рис.4.а). На рис.4 для простоты каждый искусственный нейрон представлен кружком. Более сложными и мощными по своим функциональным возможностям являются многослойные НС прямого распространения, наиболее широко в настоящее время используемые на практике. Двухслойный вариант сети показан на рис.4 б. В многослойных нейронных сетях нейроны объединяются в слои. Слой содержит совокупность нейронов с едиными входными сигналами. Число нейронов в слое может быть любым и не зависит от количества нейронов в других слоях. Внешние входные сигналы подаются по входам нейронов входного слоя (0-й слой). Далее сигналы распространяются от входа к выходу по слоям. Выходами сети являются выходные сигналы последнего слоя. Кроме входных и выходных слоев может быть один или несколько скрытых слоев. Как правило, нейроны одного слоя имеют один тип активационной функции.

2)Сети с обратными связями, в которых информация с последующих слоев передается на предыдущий (рис.4 c), d) ). Введение обратных связей в НС, с одной стороны, расширяет ее функциональные возможности, с другой стороны, может создать дополнительные проблемы (например, с устойчивостью ее функционирования).

Обратными связями могут охватываться как отдельные слои, так и несколько слоев и даже вся сеть. Наиболее часто используются сети

Хопфилда, представленные на рис.4 с).

3) Регулярные (конкурирующие) сети представлены на рис.4.e), f).

Регулярность сети состоит в том, что каждый нейрон связан определенным образом со своими соседями. Как правило, нейроны располагаются в узлах некоторой регулярной решетки (сетки), и кроме внешних входных сигналов на каждый нейрон поступают выходные сигналы в некотором смысле соседних нейронов. Понятие соседства зависит от типа используемой решетки.

8

Известные нейросети можно разделить по типам структур нейронов:

гомогенные (однородные) и гетерогенные. Гомогенные сети состоят из нейронов одного типа с одинаковой активационной функцией. В

гетерогенную сеть входят нейроны с различными активационными функциями.

Различают бинарные и аналоговые сети. Бинарные оперируют только с двоичными сигналами. Аналоговые – с произвольными сигналами.

Классифицируют синхронные и асинхронные сети. В первом случае лишь один нейрон в каждый момент времени меняет свое состояние. Во втором -

состояние меняется сразу у целой группы нейронов (или у всего слоя).

1.3 Сети прямого распространения

Сети этого типа наиболее часто используются в практических приложениях и характеризуются тем, что в них сигналы распространяются в прямом направлении – от входов к выходам.

1.3.1 Однослойные сети

Исторически первыми были разработаны однослойные сети типа персептрон и методы их обучения. Персептрон представляет собой однослойную сеть,

представленную на рис.4 а) и состоящую из нейронов, имеющих пороговые активационные функции. Данный класс НС предназначен для классификации линейно разделимых классов, в которых образы различных классов можно разделить некоторой гиперплоскостью. Персептрон, состоящий из одного нейрона, может решать задачу разделения только двух классов. Увеличивая число нейронов, можно решать задачу классификации на большее число классов.

Рассмотрим более детально один двухвходовой персептрон, показанный на рис.5.

9

Рис.5 Персептрон с 2 входами

x2

W1

x1

W2

Рис. 6 Два линейно-разделимых класса

Рассмотрим обратную задачу: есть обучающая выборка, то есть множество образов с известной для каждого образа принадлежностью к

классу. Требуется найти синаптические коэффициенты W0 ,W1 ,W2 таким

образом, чтобы образы первого класса отделялись от второго. В графической

интерпретации необходимо найти линию (или гиперплоскость),

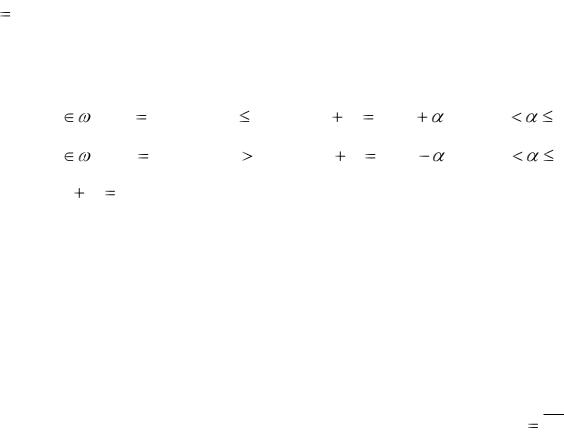
10

разделяющую образы двух классов. Для этого можно использовать,

например, классический алгоритм обучения персептрона, который представлен ниже.

Воснове данного алгоритма лежит принцип поощрения и наказания.

1.Всем весам сети присваиваются некоторые малые случайные значения

(чтобы сеть сразу не могла войти в состояние насыщения).

4. Повторение пунктов 2,3 пока результаты текущей итерации не совпадут с результатами предыдущей итерации.

Доказана сходимость данного алгоритма для линейно разделимых классов. В случае линейно неразделимых классов этот алгоритм “циклит”.

Алгоритм использует “обучение с учителем”, где учитель подает на входы персептрона входной образ и сообщает его принадлежность определенному

классу. Обучающая выборка состоит из k входных векторов X p , p 1, k , для

каждого из которых указан требуемый выходной вектор Yp . Компоненты входного вектора задаются непрерывным диапазоном значений, компоненты требуемого выходного вектора являются бинарными (0,1). Подобный подход при соответствующем кодировании образов позволяет распознавать достаточно сложные образы.

Для примера на рис.7 представлен персептрон, распознающий буквы русского алфавита. Он имеет 12 двоичных входов по числу клеток входного поля и 33 выхода, каждый из которых соответствует своей букве. Буква