
Нейросетевые технологии / АСУ Скобцов Искусственные нейронные сети лекции
.pdf
21
Видно, что здесь обучение сводится к минимизации разности между входными синапсами нейронов, поступающих с выходов нейронов
предыдущего слоя, и весовыми коэффициентами его синапсов.
Полный алгоритм обучения имеет приблизительно такую же структуру,
как и алгоритм Хебба, но на шаге 3 из всего слоя выбирается 1 нейрон,
значение синапсов которого максимально подходят на входной образ X и
подстройка весов этого нейрона выполняется по формуле (10). Таким образом, здесь реализуется принцип «победитель получает все». Именно этот подход называют конкурирующим (competitive) обучением. Приведенная процедура разбивает множество входных образов на кластеры, присущие входным данным. Здесь важнейшей проблемой является определение
нейрона-победителя. |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
Определение нейронов-победителей в сети Кохонена. |
|||||||||||
|
|
|
|
|
|
|
Рассмотрим пример сети простейшей структуры с входным вектором |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
out и матрицей синаптических весов W . Когда |
||||||||
|
|
|
, |
выходным вектором Y |
|||||||||||||||||
|
|
X |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
входной образ X подается на входы сети, активизируется только один |
|||||||||||||||||||||
выходной |
|
нейрон-победитель |
с |
вектором |
весовых |
коэффициентов |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
W j |
|
|
(W1 j ,...,Wnj ). В правильно обученной сети входные образы из одного |
||||||||||||||||||
кластера |
активизируют один и |
тот |
же выходной нейрон-победитель, |
||||||||||||||||||
соответствующий этому кластеру. |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
Обычно применяются два метода определения нейрона победителя. |
||||||||||||||
1. Первый подход основан на определении скалярного произведения |
|||||||||||||||||||||
|
|
|
|
|
|
tj * |
|
, |
|
|
|
|
|
|
(11) |
||||||
|
y j |
W |
X |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
где |
X - |
входной вектор, |
W jt - |
транспонированный j-й столбец матрицы |
|||||||||||||||||
весовых |
коэффициентов, |
|
соответствующий |
вектору |
синаптических |
||||||||||||||||
коэффициентов j-очго нейрона. Для каждого j-го выходного нейрона вычисляется скалярное произведение (11) и определяется k-й нейрон с максимальным значением (11), который считается нейроном-победителем.
При этом обычно вектора X и W j нормализуются (то есть делятся на свою

22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
длину |
|
X |
|
и приводятся к единичным векторам). Доказано, что если хотя бы |
||||
|
|
|
||||||
|
|
|
||||||
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
один из |
векторов X или W j подвергается нормализации, то процесс |
|||||||
самоорганизации приводит к связному разделению пространства данных.
Далее устанавливаются выходные |
значения нейронов yk |
1для |
нейрона- |
||||||||||||||||||||||
победителя и |
y j |
k |
0 для остальных (проигравших) нейронов. |
|
|
|
|||||||||||||||||||
|
|
|
|
Как только определяется победитель, его веса корректируются |
|||||||||||||||||||||
следующим образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Wk (t |
1) |
(x |
Wk (t |
1)) |
, |
|
|
|
(12) |
|
|||||||||||
Wk |
(t) |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
Wk |
|
x(t) Wk (t) |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
где |
|
деление |
на |
норму |
Wk |
|
x(t) Wk (t) |
сохраняет |
вектор W k |
||||||||||||||||
нормализованным. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
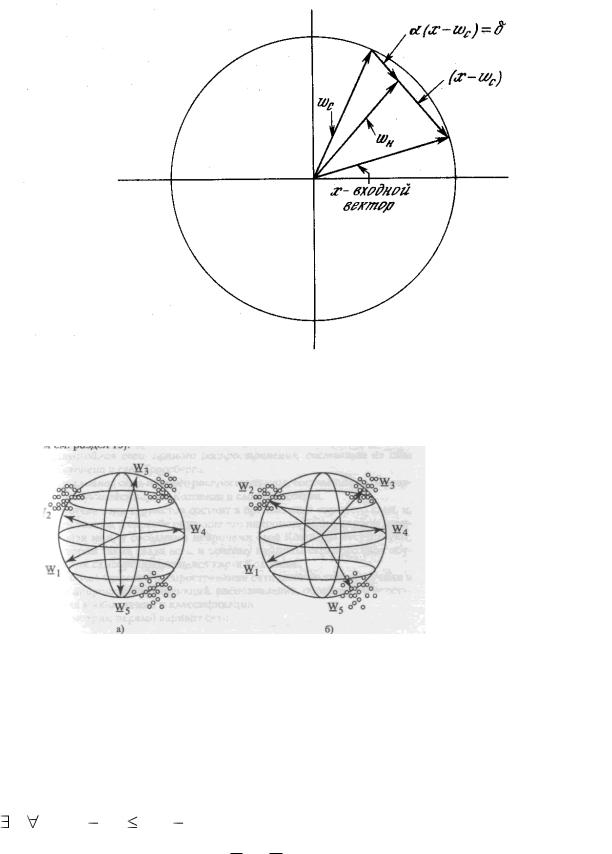
Согласно этому |
выражению вектор весов “подкручивается” в |
сторону |
|||||||||||||||||||||||
вектора x , что показано на рис.10.
Впроцессе обучения, каждый раз, когда предъявляется текущий вектор
x, определяется ближайший к нему весовой вектор нейрона победителя,
который “подкручивается” по направлению к x . В результате вектора весов нейронов вращаются по направлению к тем областям, где находится много входных образов (т.е. кластеров), что показано на рис. 11.
23
Рис. 10 Вращение весового вектора в процессе обучения (Wн – вектор новых весовых коэффициентов, Wс – вектор старых весовых коэффициентов)
Рис.11 Установление весовых векторов нейронов в центры кластеров
Второй метод определения нейрона-победителя основан на вычислении евклидова расстояния. При этом в качестве победителя выбирается k-й
нейрон для которого евклидово расстояние удовлетворяет условию:
|
|
|
|
|
|
|
|
|
|
|
|
|
k, j : |
Wk X |
|
W j X |
|
(13) |
|||||||
Очевидно, что если вектора X и W нормализованы, то этот метод дает те же результаты, что и первый. После определения победителя его веса
корректируются по той же формуле
24
1.4.4 Самоорганизующиеся карты Кохонена
Сети этого типа также рассчитаны на самообучение. В процессе обучения на вход сети подаются различные образы обучающего множества.
Сеть улавливает особенности их структуры и разделяет образы на кластеры.
Уже обученная сеть относит каждый вновь поступивший входной образ к одному из кластеров, руководствуясь некоторым критерием близости.
Сеть состоит из одного входного и одного выходного слоя и представлена на рис.9. Количество элементов в выходном слое определяет,
сколько различных кластеров система может распознать. Каждый из входных элементов получает на вход весь входной образ Х, как и в любой НС. Каждой связи приписан некоторый синаптический вес Wij , но при этом каждый
выходной нейрон соединен и с ближайшими соседями по регулярной структуре (сетке). Таким образом на выходной нейрон поступают входные сигналы Х и выходные сигналы y j соседних нейронов.
Таким образом, выходные нейроны активизируются в двумерном массиве (сетке), вид которого зависит от приложения. В процессе обучения веса нейронов выходного слоя адаптируются, т.о. что порядок или близость во входном пространстве сохраняется и в выходном слое. Образы близкие во входном пространстве отображаются в выходные нейроны, которые физически близки на заданной сетке. Таким образом, имеет место отображение, сохраняющее топологические свойства. Отметим, что внутрислойные связи играют важную роль в процессе обучения, т.к.
корректировка весов происходит только в окрестности того элемента,
который наилучшим образом откликается на очередной вход. Как и в конкурирующем обучении выигрывает тот нейрон, который имеет вес W
ближе всех к входному нейрону. Но в отличие от предыдущего случая корректируются веса не только нейрона-победителя, но и его ближайшего окружения.
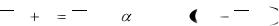
25
Обычно в качестве обучающего множества берутся случайные образы.
На текущем шаге обучения t предъявляется образ Х(t). По приведенным выше формулам определяется нейрон-победитель К. Далее его вес и веса его соседей изменяются по формуле:
W0 (t 1) Wo (t) 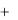 * g(0, k) x(t) Wo (t) . (13)
* g(0, k) x(t) Wo (t) . (13)
Здесь g(o,k) – убывающая функция, определенная на заданной сетке
нейронов в зависимости от расстояния между ними. Например, часто используется формула Гаусса, график которой представлен на рис.12 a).
Благодаря этому правилу образы близкие во входном пространстве признаков отображаются в выходном слое на сетке. Наряду с формулой Гаусса часто используется функция вида “мексиканская шляпа”, показанная на рис.12б). Подобная функция имеет место в живой природе при самоорганизации клеток с использованием латерального торможения.
Сеть и карта Кохонена имеет следующие недостатки: 1) метод обучения по сути является эвристическим, поскольку формально не обосновано (не сведено к задаче оптимизации); 2) конечные весовые вектора нейронов зависят от последовательности обработки входных образов; 3) при различных начальных условиях могут получиться различные результаты; 4)
некоторые параметры алгоритма обучения, такие как скорость обучения,
размер окрестности и вид функции коррекции весов необходимо изменять в процессе обучения и даже менять обучающие выборки. Поэтому часто применяют комбинированные сети, где пытаются объединить лучшие черты различных архитектур и методов обучения.
Сети Кохонена (и их современные модификации) широко применяются для сжатия данных, в частности, изображений. При этом образующая кластер группа данных представляется единственным нейроном-победителем. В этом случае достигается значительное сокращение информации, которое и называется сжатием (компрессией).

26
Рис. 12 Функции коррекции весов окружения нейрона-победителя
Допустим, что изображение размером N x N y пикселов разделяется на |
|
одинаковые кадры размером nx ny пикселов. Компоненты входного вектора |
|
X размерностью nx |
ny представляют пикселы данного кадра изображения. |
Каждая компонента |
определяет интенсивность пиксела в кадре. Сеть |
Кохонена содержит n нейронов, каждый из которых связан со всеми
компонентами |
вектора |
X. При обучении |
сети |
в данном случае |
|||||||||
|
|
|
|
1 p |
|
|
|
|
2 |
||||
минимизируется |
ошибка |
квантования |
Eq |
|
|
|
xi |
wk (i) |
|
, где wk (i) |
|||
|
|
|
|||||||||||
|
|
|
|
|
|
||||||||
p i 1 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
представляет весовой вектор нейрона – победителя в случае предъявления вектора X и p –число входных векторов. После обучения вектору X каждого кадра соответствует весовой вектор нейрона-победителя. Для похожих, но разных кадров, побеждать будет один и тот же нейрон (либо их группа).
Номера нейронов-победителей образуют кодовую таблицу, а веса этих

27
нейронов представляют средние значения, соответствующие компонентам вектора X. Поскольку число нейронов n существенно меньше количества кадров N r , то имеем значительное уменьшение объема информации для хранения изображения. Коэффициент компрессии при этом определяется [7
Осовский] следующей формулой: K y |
|
N nx nyT |
, где T и t – число битов, |
|
N |
lg 2 n nnx ny t |
|||
|
|
используемых для представления значений интенсивности и весов соответственно. Данный подход позволяет достичь степени компрессии 16
при значениях коэффициента PSNR 26-28 дб. На рис.13 представлены исходное и сжатое изображения “Барбара” (размером 512x512 пикселов). При этом использовалась сеть Кохонена из 512 нейронов. В случае 8-битового представления получена степень компрессии Kr 9.8 .
Рис.13 Сжатие изображений сетью Кохонена
1.5 Рекуррентные сети
Ранее рассмотренные сети не имели обратных связей, т.е. связей идущих от выходов нейронов к их входам. С одной стороны это хорошо, так как такие сети не могут войти в режим генерации, когда выходные сигналы все время изменяются и поэтому непригодны для использования. Но с другой
28
стороны это плохо, потому что сети без обратных связей обладают более ограниченными возможностями по сравнению с сетями, имеющими обратные связи. Самой известной рекуррентной НС является сеть Хопфилда, которая была разработана в середине 80-х годов и открыла новое направление в теории нейронных сетей. Отличительной особенностью этих сетей являются динамические зависимости на каждом этапе функционирования. Здесь изменение состояния одного нейрона отражается на всей сети, поскольку он связан обратными связями со всеми нейронами.
Если поведение многослойной сети прямого распространения можно описать системой нелинейных алгебраических уравнений, то поведение рекуррентных сетей описывается системой дифференциальных уравнений.
Можно провести аналогию с цифровыми схемами: многослойный персептрон соответствует комбинационным схемам, а рекуррентные сети последовательностным схемам (с памятью).
Сеть Хопфилда
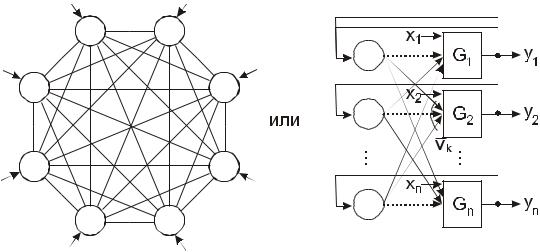
Эта сеть, как показано на рис.14, состоит из одного слоя нейронов,
количество которых равно также числу входов и входов сети.
Рис.14 Сеть Хопфилда Поменять местами и откорректировать.
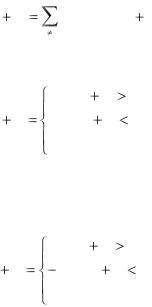
29
Каждый нейрон имеет один вход и его выход связан со всеми остальными нейронами. Поэтому эти сети часто также называют полносвязными и представляют в виде, показанном на рис.14 а). В своих ранних работах Хопфилд использовал обычную двоичную активационную функцию:
S k (t |
1) |
y j (t) *W jk |
xk |
(14) |
|
|
j |
k |
|
|
|
|
|
1, Sk (t |
1) |
Tk |
|
yk (t |
1) |
0, Sk (t |
1) |
Tk |
(15) |
yk (t), иначе
В последнее время часто применяется в качестве активационной функции следующая модификация
|
1, Sk (t |
1) |
Tk |
|
yk (t 1) |
1, Sk (t |
1) |
Tk |
(16) |
yk (t), иначе
Состояние сети определяют множество текущих значений выходных сигналов yj = 0, 1. Так как выходы нейронов с пороговой активационной функцией принимают значения 0 или 1, то текущее состояние сети является двоичным n-разрядным числом (вектором). В этом случае, очевидно, для n
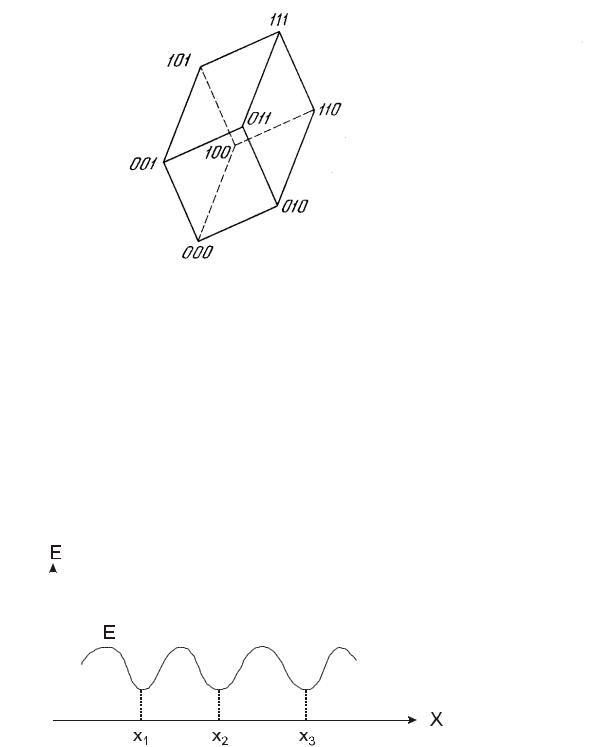
нейронов возможны 2n состояний, которые наглядно представлять вершинами двоичного (гипер) куба, что показано на рис.15.
При подаче нового входного набора сеть переходит из вершины в вершину до тех пор, пока не стабилизируется. Из всех 2n состояний только часть состояний являются устойчивыми. Устойчивая вершина определяется сетевыми весами W, текущими входами X и величиной порога Тк . Как и в других типах сетей веса между слоями можно рассматривать в виде матрицы
W. Показано, что сеть Хопфилда является устойчивой, если матрица W
имеет 0 на главной диагонали Wii=0 и симметричной - Wij = Wji.
30
Рис.15 Двоичный куб состояний сети Хопфилда
При этих ограничениях можно представить, что всевозможные состояния образуют некоторую холмистую поверхность, где впадины
(минимумы) соответствуют устойчивым состояниям (рис.16). Изменение текущего состояния при этом соответствует поведению тяжелого шарика,
катящегося по этой поверхности – он движется вниз по склону в ближайшую впадину, представляющую локальный минимум.
Рис.16 Энергетические состояния сети Хопфилда Добавить шарик
Каждая точка поверхности в этой интерпретации соответствует некоторому состоянию активности нейронов, а высота поверхности
