Нейросетевые технологии / АСУ Скобцов Искусственные нейронные сети лекции

41

Центрирование данных для каждого элемента обучающей выборки может быть выполнено по следующим формулам:

задачи и сложность проектируемой сети. Следует отметить, что часто НС с меньшим числом входов может быть более эффективной, чем сеть с большим числом входных параметров. Этот этап не является обязательным. Если,

например, эксперты определили приемлемое множество входных параметров для данной задачи, то его можно не изменять. Но в общем случае, число параметров может быть сокращено с помощью трех основных способов.

Первый способ основан на применении статистических методов или методов нелинейной динамики для определения частоты отсчетов (в случае

чувствительности для определения влияния каждого входа. Это позволяет ранжировать входные параметры и отсечь нижнюю часть списка. При этом

входа на среднее значение всех переменных, что требует предварительного нормирования данных.

В целом сокращение входов ведет к уменьшению сложности сетей,

времени обучения и часто к улучшению некоторых характеристик НС.

42

Разбиение данных на обучающую и тестовую выборки выполняется перед этапом обучения (обычно 2/3 данных выделяется на обучающее множество и 1/3 – на тестовое). Основным требованием является репрезентативность, т.е эти множества должны правильно отражать процесс,

из которого извлекаются данные. Непосредственно обучение НС производится с использованием обучающего множества и заключается, как было рассмотрено ранее, в поиске значений синаптических весов, которые дают минимальную ошибку между требуемыми и фактическими значениями выходов сети (в случае обучения с учителем). Очевидно, на обучающем множестве при наличии достаточного числа нейронов ошибка обучения может быть достигнута достаточно малой. Но это еще не говорит о том, что для остальных данных ошибка будет также малой. Поэтому обученная сеть проверяется на тестовом множестве. Способность НС учиться на обучающем множестве и показывать хорошие результаты на данных,

которые относятся к тому же множеству, но не участвовали непосредственно в процессе обучения называется обобщением.

Способность к обобщению основана на большом числе кодовых комбинаций входных данных по сравнению с используемыми для обучения.

Например, для двоичной нейронной сети с n входами возможно 2n входных векторов. Если для обучения использовалось m наборов, то остальные (2n -

m)характеризуют потенциально возможный уровень обобщения.

Существует тесная связь между числом синаптических весов (связей) в сети и числом образов в обучающей выборке. Очевидно, что если бы целью обучения было просто запоминание образов обучающей выборки, то число образов могло бы быть равно числу весов. В этом случае каждый синаптический коэффициент соответствовал бы одной обучающей паре (X, Yd). Но, такая сеть, очевидно не будет обладать способностью к обобщению.

Для приобретения такой способности сеть должна обучаться на избыточном множестве данных. На погрешность обобщения влияет отношение числа образов в обучающей выборке к числу весов сети. Экспериментально

43

показано, что высокие показатели обобщения достигаются тогда, когда число образов в обучающей выборке в несколько раз превышает т.н. меру Vcdim,

которая характеризует сложность сети и количество ее весов.

Качество обобщения определяют посредством наблюдения ошибки,

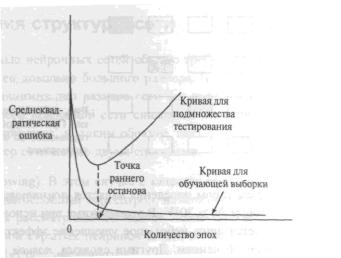
вычисленной на тестовом множестве. Если по прошествию определенного числа итераций обучения ошибка на обучающем множестве падает почти до нуля, а ошибка обобщения (на тестовом множестве) снова начинает расти

(как показано на рис.19), то это говорит, как правило, о переобучении. В

этом случае сеть обучается больше шумам, чем истинной зависимости,

которую необходимо определить. Очевидно, что в такой ситуации обучение лучше остановить раньше, не дожидаясь переобучения. Это можно сделать путем использования тестового множества для определения момента “ранней остановки», что требует, однако, проверки качества обучения еще на одном

“подтверждающем множестве”. Метод ранней остановки иногда дает лучшие результаты по сравнению со стандартным обучением, является более быстрым и обычно используется в сетях, где число весов существенно превышает размер выборки данных.

Рис.19 Ошибка обучения на обучающем и тестовом множестве

Обучение нейронной сети в большинстве случаев представляет собой автоматизированный процесс, в котором только после его окончания требуется участие специалиста для оценки результатов. Естественно, часто

44

может требоваться корректировка, создание дополнительных сетей с другими параметрами и т.д., однако всегда есть возможность оценить работу системы на любом этапе обучения, протестировав контрольную выборку.

Как отмечалось выше, обучение НС выполняется фактически за два этапа:

1)Обучение на обучающем множестве пока не выполнено одно из условий останова:

а) ошибка на обучающем множестве становится меньше заданной величины;

б) ошибка перестает изменяться в течение определенного числа итераций;

в) достигнута верхняя граница числа итераций обучения.

2)проверка правильности функционирования сети на тестовом множестве.

Если ошибка обобщения больше заданной величины, то увеличивается либо число итераций при обучении, либо количество образов в обучающем множестве или модифицируется архитектура НС.

Качество обученной сети обычно оценивается по следующим критериям:

1)эффективность модели;

2)эффективность функционирования сети;

3)устойчивость;

4)стабильность.

Эффективность модели определяет качество обученной сети исходя из полученных результатов на обучающем множестве путем сравнения требуемых значений выходов с реальными значениями. Эффективность функционирования оценивается на тестовом множестве также путем сравнения выходных сигналов (требуемых и фактических). Следует отметить, что нет гарантии, что эти показатели (способность обобщения)

будут поддерживаться в будущем. Поэтому важно проверить устойчивость НС во времени - в различные временные периоды, в качестве которых могут

45

выступать перекрывающиеся или не перекрывающиеся окна изменяющихся размеров. Стабильность обученной сети оценивается на окнах переменной длины. Обычно для этого используется метод Монте-Карло на множестве временных интервалов, каждый из которых имеет случайные точки начала и окончания.

Идентификация выходных индикаторов и их кодирование является важным этапом в проектировании НС. Выбор выходных параметров НС существенно зависит от решаемой задачи и применяемого метода обучения НС. При обучении с учителем значения выхода сравнивается с желаемым значением. Для задач предсказания будущих цен, уровня производства или

желательно выбрать такие выходные параметры, которые соответствуют используемому временному окну. Например, если система учета использует ежедневную отчетность, то прогнозирование также должно производиться на этот период.

В случае задачи классификации или распознавания образов даже для одной задачи может быть различное число выходных индикаторов,

принадлежит распознаваемый текущий образ (по принципу “победитель забирает все”). В этом случае удобно вводить и нечеткую интерпретацию.

Например, выходной сигнал после масштабирования в отрезок [0,1] может интерпретироваться в качестве значения функции принадлежности к классу,

определяемому данным выходным нейроном. Очевидно, для большого числа классов этот метод требует большого количества выходных нейронов, что конечно является существенным недостатком.

46

Иногда для сетей, использующих двоичные сигналы 0,1 (или –1,1)

применяется знаковая интерпретация, которая для M классов требует log2M

выходных нейронов. При этом совокупность выходных сигналов y1, ,…,yM ,

интерпретируется как номер класса. Например, выходные значения нейронов

(101) интерпретируются как номер класса – 5. Таким образом, здесь M

нейронов позволяют интерпретировать 2M классов (в отличие от M классов в

предыдущем случае).

Порядковая интерпретация [3] позволяет еще больше повысить число интерпретируемых классов – для M нейронов описать принадлежность к M!

классам. Для этого можно выполнить сортировку выходных сигналов y1, ,…, yM по величине сигнала (1 соответствует самому малому сигналу, а M –

можно рассматривать в качестве слова, кодирующего номер класса.

Очевидно, всего возможно M! перестановок, что и определяет число интерпретируемых классов. При этом ошибка выходного сигнала должна быть меньше 1/M.

2.2 Основные задачи, решаемые с применением нейронных сетей

Нейронная сеть, прежде всего, является универсальным апроксиматором нелинейной векторной функции нескольких переменных Y=f(X), где X-

входной и Y выходной вектор. Постановка многих практических задач может быть сведена к именно к аппроксимационному представлению. Необходимо построить такое отображение X Y , чтобы на каждый возможный входной сигнал X формировался правильный выходной сигнал в соответствии: а) со всеми примерами обучающей выборки; б) со всеми возможными входными

47

сигналами, которые не вошли в обучающую выборку (что значительно сложнее).

Именно поэтому, нейросети находят широкое применение при решении многих проблем, к которым относятся: аппроксимация и интерполяция, распознавание и классификация образов и изображений,

сжатие данных, прогнозирование, идентификация, управление,

ассоциативная память и многие другие.

В случае обучения с учителем отображение частично задается с помощью обучающей выборки – множества пар (Xi,Yi). Число этих пар

(обучающих примеров), как правило, существенно меньше числа возможных сочетаний входных значений. Рассмотрим прикладные возможности НС.

Задача классификации(распознавания).

В этом случае X – некоторое представление образа (в пространстве признаков), а Y – номер класса, к которому принадлежит этот образ. Для определенности предположим, что имеется набор данных, каждый из которых представляет m-мерный вектор X. Таким образом, матрица исходных данных состоит из n строк и m столбцов. На входы сети подаются поочередно наборы данных. То есть каждый вход соответствует компоненте входного вектора. Каждый выход нейросети соответствует своему классу

(для M классов, как правило, используется M выходов). Задачей НС является разделение исходных данных на группы (классы) в некотором смысле похожих объектов (образов). Эта задача может быть решена с помощью НС различных типов, например, многослойной нейросетью с прямым распространением путем обучения с учителем. С другой стороны при решении этой задачи можно использовать сеть (или карту) Кохонена с использованием обучения без учителя. В последнее время для этих целей все чаще применяются сети радиального базиса.

В случае многослойного перцептрона количество слоев, как правило, не превышает трех. Для классификации используются выходные переменные обычно с применением двух видов кодирования: 1) бинарном;

48

2) 1- из M. В случае бинарного представления выходной слой содержит один нейрон, выход которого может принимать два значения (0 или 1). При использовании кодирования 1- из M каждому классу соответствует свой нейрон, значение выхода которого равно 1 при нулевых сигналах остальных нейронов. Например, для трех классов имеем следующие коды выходов НС:

(100), (010), (001). В режиме распознавания каждый из выходных нейронов имеет числовые значения в интервале от 0 до 1. Для определения класса необходимо определить, достаточно ли близки выходные значения к 0 или 1.

На практике, как правило, допускается расхождение в пределах 5%, что вполне достаточно для большинства практических задач.

Как отмечалось, при классификации могут использоваться и самообучающиеся сети (или карты) Кохонена. Это подход применяется,

прежде всего, для предварительного анализа данных. При этом на этапе обучения похожие в некотором смысле данные объединяются в кластеры. На этапе распознавания подаваемый входной образ относится к одному из известных классов. Следует отметить, что в том случае, когда входной вектор

«не похож» на известные НС, можно сформировать для него новый класс.

Задача прогнозирования.

Взадачах прогнозирования в качестве входных сигналов X

используются временные ряды, представляющие значения контролируемых параметров на некотором интервале времени. В качестве выходных сигналов

Y (НС) обычно выступает некоторое множество переменных, являющееся подмножеством переменных входных сигналов. Здесь целью является прогноз будущих значений переменной на основе ее предыдущих значений.

Прогнозирование временных рядов часто сводится к регрессии. Следующее значение ряда прогнозируется на основе некоторого числа его предыдущих значений. При идентификации таких закономерностей, обычно применяется метод скользящих окон, который использует два окна Wi и W0

фиксированных размеров n и m, скользящих вдоль временной оси t. Для фиксированного размера окна последовательность предыдущих значений

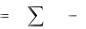
49

Wi0, …,Win связана с последовательностью будущих значений Wo0, …,Wom .

Вид связи определяется установленными данными. Далее для поиска двух конфигураций значений могут быть использованы различные методы. При использовании НС пара Wi -> W0 принимается в качестве обучающего

вектора. Оба окна скользят вдоль временного ряда с фиксировнным размером шага s. Получающиеся пары используются в качестве элементов обучающей выборки. Далее, НС обучается на этой выборке, извлекает скрытые закономерности и на этой основе строит оценку прогноза.

Применяются два основних вида прогнозирования:

1)Многошаговый прогноз, используемый при необходимости долгосрочного прогноза, цель которого состоит в идентификации общин тенденций и наиболее важних поворотних точек во временном ряду. При этом для предсказания временного ряда в фиксированный период используется конфигурация текучих значений. Затем прогноз снова вводится в сеть для прогнозирования следующего периода.

2)Одношаговый прогноз, где в отличие от предыдущего случая повторно вводить спрогнозированные ранее данные не требуется. НС предсказывает значение ряда на какой-либо момент времени и для каждого последующего прогнозного значения использует фактическую

величину, а не значение, которое было предсказано ранее.

При решении задачи идентификации X и Y представляют входные и выходные сигналы системы. В этом случае Y=f(X) описывает соотношение между входами и выходами в неизвестной системе без памяти (инвариантной во времени). Тогда обучающая выборка – множество пар {Xi,Yi} может быть использована для обучения НС, которая представляет модель этой системы. Разность (di - yi) между требуемым откликом di и фактическим выходом yi составляет вектор ошибки сигнала ei , который используется для определения параметров сети при минимизации среднеквадратичной

50

В задачах управления входом X является множество контролируемых параметров управляемого объекта, а выход Y определяет управляющее воздействие на объект. Системы управления, в которых применяются НС,

являются одной из возможных альтернатив классических методов управления.

Одним из первых методов нейросетевого управления является метод предложенный Уидроу, который основан фактически на “копировании” существующего контроллера. Архитектура такой системы управления показана на рис.20 [НС в управлении??]. Автор назвал его методом построения экспертной системы за счет получения знаний

Рис. 20. Копирование существующего контроллера

Сейчас разработаны и широко используются на практике различные архитектуры нейросетевого управления. В этом случае, назначением нейросетевого контроллера является выработка адекватного управляющего сигнала управления динамикой состояний объекта ( переход от начального состояния до требуемого конечного состояния должен происходить по оптимальной траектории). Контроль состояния объекта и вид нейросетевого контроллера зависят от выбранного алгоритма обучения и структуры системы управления. Наиболее распространенными на практике являются: 1)