Нейросетевые технологии / АСУ Скобцов Искусственные нейронные сети лекции

31

определяет “энергию” этого состояния, которую формально можно определить следующим образом:

Wij - вес от выхода нейрона i ко входу j; yj - выход j-го нейрона;

хj - вход j-го нейрона;

Тj - порог j-го нейрона.

Можно показать, что любое изменение состояния одного нейрона (при фиксированных значениях входов), либо уменьшает энергию, либо оставляет еѐ без изменения. Вследствие непрерывного стремления к уменьшению энергии в результате сеть должна достичь состояния, в котором функция энергии Е имеет min (хотя бы локальный) и прекратить изменение. Такое состояние сети является устойчивой. Таким образом, сеть устанавливается в устойчивое состояние, а не входит в режим генерации. Отметим, что если связь между некоторыми нейронами имеет большой положительный вес, то состояния, в которых данные нейроны активны, соответствуют низкому уровню энергии, и именно в такие состояния будет стремиться перейти сеть.

Наоборот, активизация нейронов с отрицательной связью добавляет к энергии сети большую величину, поэтому сеть избегает таких состояний. Эта интерпретация основана на известной в физике модели Изинга, где совокупность взаимодействующих магнитных диполей (спинов) стремится перейти в такое энергетическое состояние, в котором суммарная энергия минимальна.

Следует отметить, что одна сеть (с одними и теми же значениями весовых коэффициентов) может хранить и воспроизводить множество различных образов – эталонов. При этом каждый эталон соответствует своему энергетическому минимуму и является атрактором, вокруг которого существует область притяжения. Систему с множеством атракторов, к

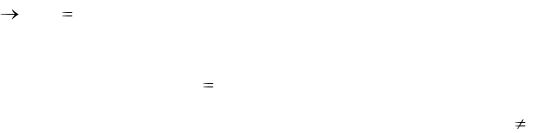
32

которым она тяготеет, можно рассматривать как содержательно адресуемую память, т.е. ассоциативную память.

Ассоциативная память с успехом может быть реализована с помощью рекуррентных НС с обратными связями, например, сетью Хопфилда.

Напомним, что ассоциативная память (associative memory) представляет собой распределенную память, которая обучается на основе ассоциаций (как

это происходит в мозгу живых существ). Различают два типа ассоциативной

запоминается множество эталонных (неискаженных) образов (например,

изображения цифр 0,1, …,9). Затем в режиме распознавания на сеть подаются неполные или зашумленные образы (например, искаженное

изображение цифры). При распознавании сеть по зашумленному образу

должна найти наиболее близкий из запомненных эталонных образов и

выдать его на выход сети. При этом фактически используется обучение без

учителя. Это показано на рис.17, где в верхней части рисунка представлены эталонные изображения цифр, а в нижней - их искаженные изображения.

В случае гетероассоциативной памяти произвольному набору входных образов ставится в соответствие другой произвольный набор выходных

сигналов. Настройка этой сети производится по методу обучения с учителем.

где q определяет емкость сети (число хранимых образов). В

33

и размерность выходных векторов может отличаться от размерности входных.

Рис. 17 Эталонные (сверху) и искаженные (снизу) изображения цифр

Пусть x является стимулом – зашумленной или искаженной версией

ассоциативная память при восстановлении образа сделала ошибку.

Число q эталонных образов, которые можно хранить в ассоциативной памяти, называется емкостью памяти. При проектировании ассоциативной

34

памяти стремятся максимально увеличить ее емкость и проверить, чтобы

большая часть запомненых образов восстанавливалась коректно.

Чтобы организовать ассоциативную память с помощью нейронной сети с обратными связями, на этапе обучения веса должны выбираться так, чтобы образовались энергетические min в запоминаемых эталонах -

соответствующих вершинах единичного гиперкуба состояний сети.

Хопфилд разработал ассоциативную память для нейронов с непрерывными выходами. В общем случае любой сигнал может быть описан

(вспоминает) какой либо образец на основе предъявляемых ей идеальных

данных еѐ выходы будут содержать идеальный объект Y X k . Если,

например сигналы представляют собой некоторые данные с выхода сети можно увидеть картинки полностью совпадающие с одним из идеальных образов.

Обучение сетей Хопфилда

До этого мы рассмотрели два способа обучения - с учителем и без

него. Строго говоря, обучение сетей Хопфилда не попадает ни в один из них.

В данном случае весовые коэффициенты Wij рассчитываются один раз перед началом функционирования сети на основе информации о запоминаемых данных, и все обучение фактически сводится к этому расчету. Из компонент идеальных образцов вычисляется по несложным правилам значение всех коэффициентов сети. Итак, обучение сводится к инициализации весов коэффициенты, которые устанавливаются следующим образом:

0, i j.

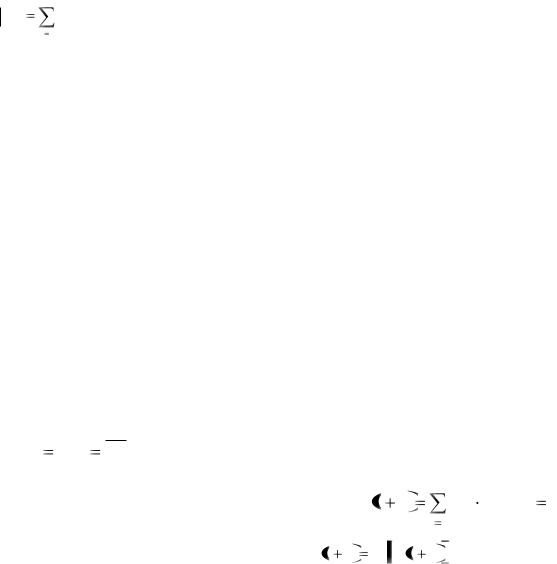
35

Здесь суммирование выполняется по всем запоминаемым образцам, при этом из каждого образца выбирается i-я и j-я компонента, которые перемножаются между собой.

В векторном виде это можно представить так

Приведенное правило вычисления коэффициентов можно интерпретировать как правило обучения по Хеббу. Как только веса сети Wij найдены, сеть

"готова к употреблению". Она должна выдать на выходы идеальный образ по заданному входному вектору, который может быть частично неправильным (искаженным). Для этого выходам сети сначала придают значения входного вектора, который должен быть распознан. Затем он убирается и сети предоставляется возможность "расслабиться" опустившись при этом в ближайший min, который должен содержать соответствующий эталонный образ.

Алгоритм состоит из следующих этапов:

1. На входы сети подается неизвестный сигнал, который вводится непосредственно установкой выходов следующим образом:

yi (0) xi , i 1,n.

3.Выполняется проверка, изменились ли выходные значения yi за последнюю итерацию. Если да (неустановившееся состояние) то переход на п.2. Если сеть попала в устойчивое состояние, то она выдает выходной вектор, ближайший (но имеющий сходство не меньше определенного порога) из запомненных к эталонному сигналу.

Если среди хранимых эталонов нет похожих образцов, то выдается соответствующее сообщение.

36

Важнейшим параметром ассоциативной памяти является ее емкость – максимальное количество запоминаемых эталонов, которые распознаются с допустимой погрешностью . Показано [7] (Осовский с.180), что при использовании для обучения приведенной выше методики (Хебба) для

0.01 максимальная емкость памяти составляет 0.138n (от числа нейронов, образующих сеть). Таким образом, правило Хебба здесь не эффективно, поэтому разработаны другие методы [7] (Осовский с.181)

обучения, которые позволяют повысить емкость памяти.

По окончанию вычисления синаптических весов их значения

“замораживаются” и сеть может быть использована непосредственно для распознавания.

Существует три основных применения сетей этого типа:

1.Распознавание образов

2.Ассоциативная память

3.Решение задач комбинаторной оптимизации.

Последнее применение совершенно нестандартно для нейронных сетей. Оно основано на том, что из условий задачи формируется функция энергии E и

после установки сети в необходимое начальное состояние она “отпускается” и стремится достичь состояния минимума энергии, которое и дает решение задачи. Таким образом, с успехом решаются многие проблемы, например,

задача коммивояжера, которая является базовой задачей комбинаторной оптимизации и имеет большое практическое значение.

37

2. Прикладные аспекты использования нейросетей

Для решения некоторой задачи с применением нейросетевых технологий необходимо выполнить априорный анализ объекта исследования, который включает в себя обобщение опыта и специальных знаний о нем, крайне желательно получение предварительных рекомендаций экспертов в данной области, изучение специальной технической и патентной литературы и известных прототипов, сбор необходимых данных и формирование обучающей и тестовой выборки для проектируемой НС.

Специалист в данной предметной области, как правило, в состоянии самостоятельно поставить задачу, более того, никто, кроме него, не сможет сделать это лучше. Сбор материала желательно также осуществлять с помощью специалиста в этой области.

4.Отбор наиболее существенных переменных.

5.Разбиение данных на обучающую и тестовую выборки. Производится сбор набора примеров для обучения сети, каждый из которых представляет массив входных данных с соответствующими ему заранее известными ответами.

6.Разработка архитектуры нейронной сети. Данный этап не требует проведения статистических вычислений в том случае, если задача укладывается в стандартную схему (в большинстве случаев). Если задача

38

нестандартная, требуется адаптация структуры нейросети и методов

вычисления функции ошибки при обучении.

7.Обучение нейросети. Создание интерфейса. Выполняется также как и для классических экспертных систем с учетом инструментальных программных средств для работы с нейронными сетями.

8.Оценка нейросети, отладка и тестирование. На данном этапе выполняется,

в основном, отладка работы программы, т.к. тестирование чаще производится в процессе обучения сетей.

9.Доучивание. Этап, характерный только для обучающихся систем. При создании нейросетвых систем довольно редко возможно сразу собрать достаточное количество данных для хорошего обучения сети. Поэтому,

создавая нейросистему, разработчик определяет наилучшие параметры сети и проводит начальное обучение. В последующей эксплуатации пользователь должен иметь возможность доучивать систему в условиях

реальной работы и реальных данных, передавая ей (появляющийся новый)

опыт.

Более того, коренное отличие методологии проектирования нейросетевых систем от традиционных состоит именно в том, что система никогда не создается сразу готовой, и никогда не является полностью законченной,

продолжая накапливать опыт в процессе эксплуатации.

Далее рассмотрим некоторые этапы более подробно.

Сбор данных включает извлечение качественных (достоверных) данных из доступных источников, содержащих достаточно полную информацию в данной проблемной области. На этом этапе выполняется также, если это необходимо, восстановление пропущенных данных и их очистка

(фильтрация). В больших объемах данных, как правило, пропущены некоторые интервалы наблюдений или собрана информация не по всем параметрам. При восстановлении данных обычно используются два подхода: во-первых исключение строки или столбца матрицы данных с пропущенными значениями; во-вторых восстановление данных, например,

39

по средним значениям соседних элементов. Очистка (фильтрация) данных состоит в устранении нежелательных шумов, которые могут существенно исказить реальную картину. Необходимо также контролировать поступающие значения и отсекать те данные, которые выходят за пределы диапазона изменений соответствующих параметров. Процедура выборки часто сводится к снижению популяции данных, которая должна удовлетворять некоторым критериям. К ним относятся уменьшение стоимости анализа, ускорение времени обучения и т.д. При формировании выборки важно, чтобы необходимые данные извлекались пропорционально сложности обучения. Часто при выборочной стратегии для ускорения обучения и нейросетевого моделирования объем выборки снижается до 10%

от имеющихся всех данных. При этом выборка должна оставаться репрезентативной и подчеркивать специфические черты данных.

Преобразование и анализ данных существенно зависит от решаемой задачи и требует ответа на следующие вопросы:

1)какие переменные оказывают влияние на выходы сети;

2)какие переменные используются в известных прототипах (если они есть) или предлагаются экспертами;

3)какова приемлемая частота отсчета данных;

4)какой вид преобразования данных необходим.

Преобразование данных направлено на улучшение классификации, переход от нелинейных задач к линейным, и концентрацию обработки только в части входного диапазона. Часто для удобства работы проводят статистическую обработку данных, исключение аномальных данных (фильтрация),

нормирование и центрирование данных для того, чтобы значение каждой компоненты входного вектора лежало в диапазоне [0,1] или [-1, 1].

40

Где [a,b] представляет заданный диапазон изменения входных сигналов, а

[xmin , xmax ]- диапазон изменения конкретной входной переменной, p- значение преобразованного входного сигнала. Обычно [a,b] равны [0,1] или [-1, 1].

Очевидно, после этого преобразования значения всех переменных лежат в диапазоне [a,b]. Следует отметить, что для активационных функций типа сигмоид (гиперболический тангенс) диапазон выходных значений [0,1] ([-1,

1]) может представлять определенные трудности (на концах диапазона производная имеет малые значения и скорость обучения резко падает) и

иногда целесообразно проводить масштабирование таким образом, чтобы диапазон изменения выхода составлял [0,2 - 0,8] ([-0,8 – 0,8]).

Кодирование параметров требует учета типа переменных – непрерывные или дискретные, количественные или качественные.

Качественные переменные могут принимать конечное число значений,

например, состояние больного можно оценить как (очень тяжелое, средней тяжести, удовлетворительное и т.п.). Если качественная переменная может принимать только два значения, то она называется бинарной.

Взависимости упорядоченности качественных признаков

(упорядоченные, частично упорядоченные, неупорядоченные) существенно различается их кодирование. Например, упорядоченные признаки кодируются в шкале порядка. Так как произвольные состояния неупорядоченного признака не связаны отношением порядка, их нельзя кодировать различными значениями. Отсюда при кодировании неупорядоченных качественных признаков лучше применять шкалу наименований и рассматривать переменные, которые соответствуют данным признакам, как номинальные

В случае кодирования количественных переменных, которые

принимают числовые значения, необходимо учитывать семантику

признаков, расположение значений в интервале значений, точность измерений и т.п.