6.2.4. Метод комбинированный

Соединил метод хорд и метод Ньютона. На каждом этапе этого метода находят значение по недостатку и значение по избытку корня нелинейного уравнения.

Рассмотрим случай

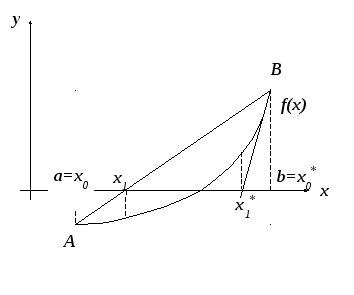
Рис. 6.6

Для метода хорд неподвижен конец b, , то естьх₀=а.

Для метода касательных так как

Метод хорд применяется на каждом шаге к новому отрезку

(6.10)

(6.11)

Вычисления прекращаются, если

Тогда корень уравнения по окончании вычислений лучше взять за среднее арифметическое

(6.12)

Комбинированный метод можно рассматривать иначе

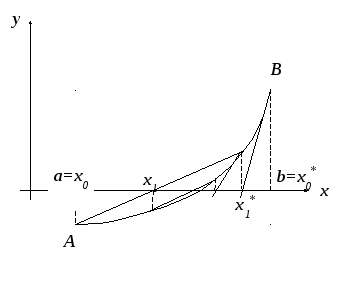
Рис. 6.7

→по методу касательных

(6.13)

по методу хорд.

Метод хорд на каждом шаге применяем к отрезку

(6.14)

Условие окончания и ответ аналогичен комбинированному методу для рис. 6.6

6.2.5. Метод итераций

Суть метода заключается в следующем

Исходное уравнение

заменим равносильным уравнением

. (6.15)

Выберем каким-либо способом приближенное значение корня х₀ и подставим его в правую часть преобразованного уравнения

и далее

То есть,

(6.16)

Процесс итерации следует продолжать до тех пор, пока для двух последовательных приближений не будет обеспечено выполнение неравенства

Преобразование исходного уравнения необходимо выполнить таким образом, чтобы

(6.17)

на отрезке [a,b], что является условием сходимости.

6.2.6. Особенности решения алгебраических нелинейных уравнений

Вспомним предварительно известные из курса алгебры некоторые свойства алгебраических уравнений с действительными коэффициентами в виде

1. Уравнения степени n имеет n корней, среди которых могут быть как действительные, так и комплексные.

2. Число положительных действительных корней меньше или равно числу перемен знаков в последовательности коэффициентов a₀, a₁,…, a_n. Заменяя х на (-х) в уравнении таким же способом можно оценить число отрицательных действительных корней.

3. Комплексные корни образуют комплексно-сопряженные пары, то есть каждому корню x=c+id соответствует x=c-id

Одним из способов решения алгебраического уравнения является метод понижения порядка. Он состоит в том, что после нахождения какого-либо корня x=c данное уравнение можно разделить на x-c, понизив тем самым его порядок на 1 до n-1 степени.

Для уменьшения погрешностей лучше сначала находить меньшие по модулю корни многочлена и сразу удалять их из уравнения. Поэтому, если отсутствует информация о величинах корней, в качестве начальных приближений принимают числа 0, ±1 и так далее.

Изложенные методы решения нелинейных уравнений могут быть использованы и для нахождения комплексных корней многочлена. Если в качестве начального приближения корня взять комплексное число, то последующие приближения и окончательное значение корня могут быть комплексными. Комплексные корни попарно сопряженные и при их исключении порядок уравнения уменьшается на два, поскольку оно делится сразу на квадратный трехчлен.