6.2.1. Метод деления отрезка пополам. Метод половинного деления. Метод дихотомии. Метод бисекции.

Один из простейших методов. Довольно медленный, однако он всегда сходится, то есть при его использовании решение получается всегда, причем с заданной точностью (разумеется, в рамках разрядности ЭВМ). Требуемые обычно большее число итераций по сравнению с некоторыми другими методами не является препятствием к применению этого метода, если вычисление значения f(x) несложно.

Суть метода в следующем:

В качестве х₁ принимаем середину отрезка [a,b]

(6.4)

Далее исследуем функцию f(x) на отрезках [a,х₁], [х₁,b], точнее на концах этих отрезков. Тот из них, для которого выполняется теорема 1, содержит искомый корень. Отрезок, для которого теорема 1 не выполняется, отбрасываем.

То есть, если f(a)f(x₁)<0, то b=x₁,

отрезок [х₁,b] отбрасываем, если f(x₁)f(b)<0, то a=x₁, отрезок [a,х₁] отбрасываем.

Далее в качестве x₂ принимаем середину нового отрезка и так далее. Таким образом, после каждой итерации, отрезок, на котором расположен корень, уменьшается вдвое, то есть после n итераций он сокращается в 2ⁿ раз.

Итерационный процесс продолжаем до тех пор, пока значение функции

(6.5)

или длина отрезка [a,b] на i-ой итерации

не станет меньше по модулю некоторого заданного малого числа.

6.2.2. Метод пропорциональных частей Метод хорд

Алгоритм метода хорд и метода дихотомии похожи, но метод хорд в ряде случаев дает более быструю сходимость итерационного процесса. Успех применения этого метода, как и метода дихотомии, гарантирован.

Рис. 6.1

выпукла вниз выпукла вверх

В данном методе процесс итераций состоит в том, что в качестве приближения к корню принимают значения х₁, х₂,…, являющиеся абсциссами точек пересечения хорды АВ с осью абсцисс.

Уравнение хорды АВ

Для точки пересечения хорды с осью 0х на первой итерации координаты х=х₁ и у=0.

Далее рассматривая отрезки [a,х₁], [х₁,b], оставляем тот из них, для которого выполняется теорема 1, второй при этом отбрасываем.

Итерационный процесс продолжается до тех пор, пока, как и для метода дихотомии,

Для рассмотренного рисунка видно, что неподвижным на всех итерациях является конец b отрезка [a,b].

Для случая

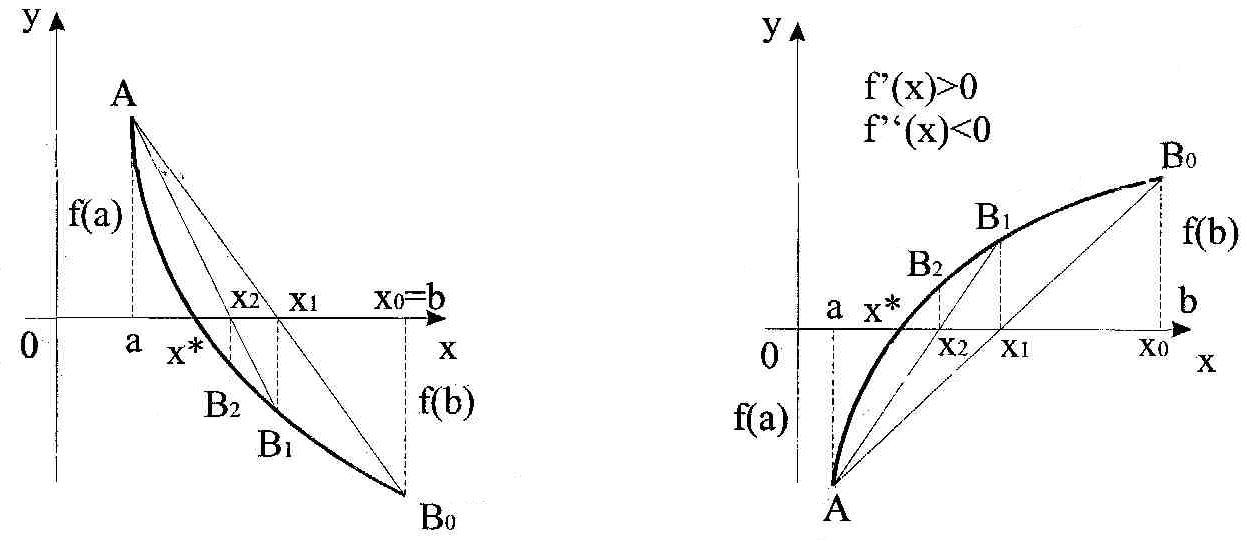
Рис. 6.2

выпукла вниз выпукла вверх

неподвижным остается конец а отрезка [a,b].

Рассмотрим формулу метода хорд отдельно для каждого из случаев 1 и 2.

Для случая 1 (неподвижен конец b)

(6.6)

Для случая 2 (неподвижен конец а)

(6.7)

Для того, чтобы воспользоваться этими формулами без анализа графической картины функции f(x) необходимо следовать правилу

- неподвижен тот конец, для которого знак функции совпадает со знаком ее второй производной.

неподвижен a, x₀=b

неподвижен b, x₀=a

Естественно при этом требуется вычислить значении

При использовании этих формул условие окончания вычислений

или

6.2.3. Метод Ньютона. Метод касательных

Алгоритм метода Ньютона схож с алгоритмом метода хорд. Отличие состоит в том, что на некоторой итерации вместо хорды проводится касательная к графику функции f(x) при x=a или x=b и отыскивается абсцисса точки пересечения касательной с осью 0х.

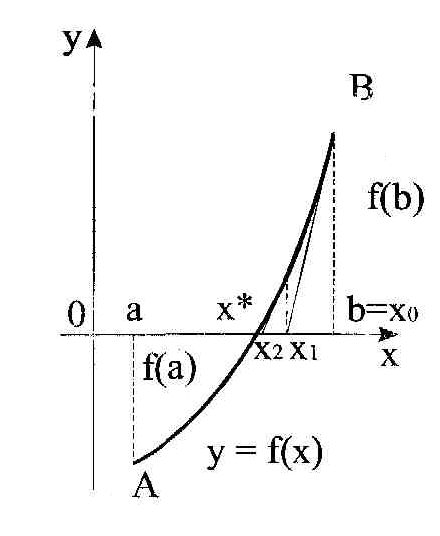
Рис. 6.3

Уравнение касательной по формуле Тейлора

Для точки пересечения касательной с осью 0х на первой итерации координаты х=х_1, у=0.

Далее проверяем значения функции на концах отрезка [a,х₁], [х₁,b] и оставляем тот из концов отрезка, для которого выполняется теорема 1.

На рисунке 6.3 видно, что для данного поведения функции конец а отрезка [a,b] остается неподвижным.

На рисунке 6.4 неподвижным остается конец b.

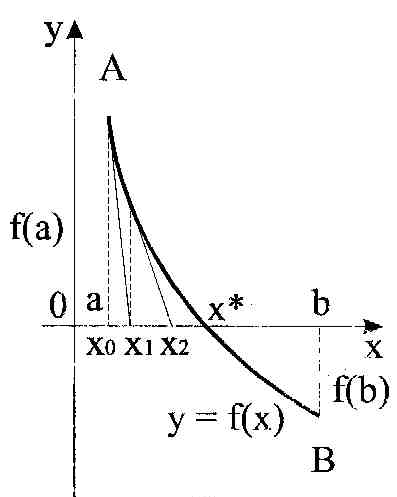
Рис. 6.4

Таким образом, также как и для метода хорд, можно написать формулу, связывающую между собой два соседних приближения корня

(6.8)

При этом в качестве х₀ принимается тот из концов отрезка [a,b], для которого выполняется условие: значение функции и значение второй производной одинаковы по знаку

x₀=а

x₀= b

Итерационный процесс продолжается до выполнения условий

или

Из анализа расчетной формулы метода Ньютона следует, что

1. должно быть ,

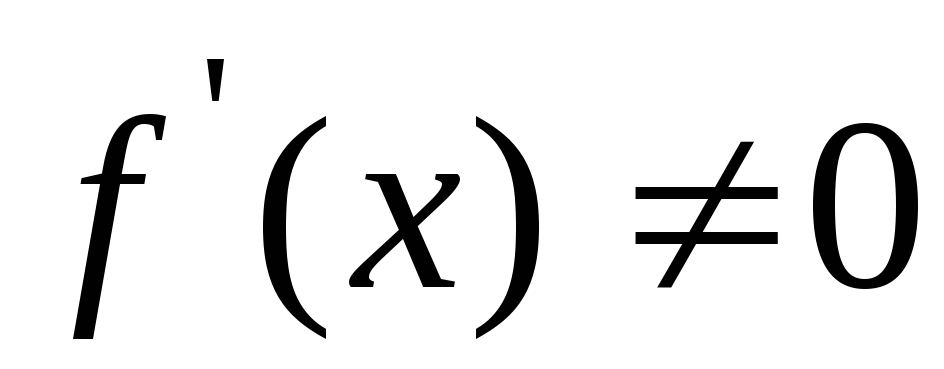2. на каждой итерации объем вычислений больший, чем в рассмотренных ранее методах дихотомии и хорд, так как требуется вычислить не только 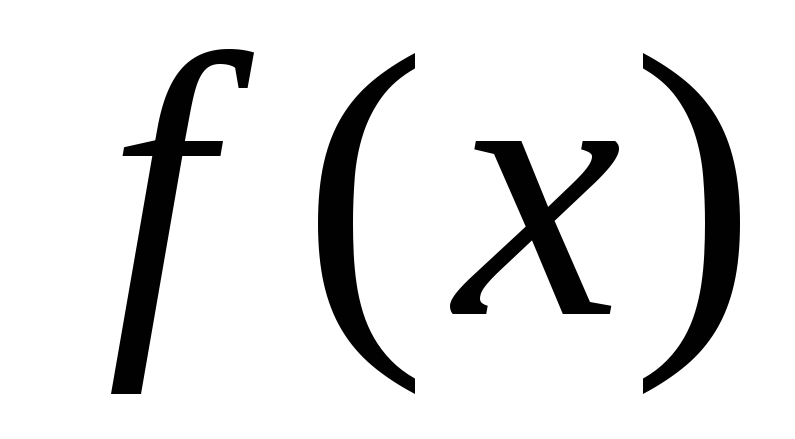, но и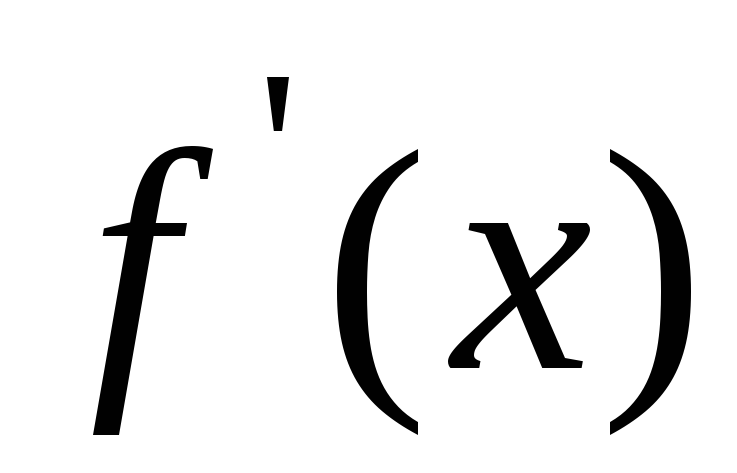. Однако скорость сходимости этого метода значительно выше, чем в других методах.

Уменьшить количество вычислений на каждой итерации позволяет видоизмененный метод Ньютона, для которого расчетная формула имеет вид

, (6.9)

то есть для получения этой формулы предположили, что . Данное предположение допустимо, если мало изменяется на отрезке [a,b].

Теоретически это означает, что мы заменяем касательную в точках с абсциссой прямыми, параллельными касательной проведенной к точке с абсциссой.

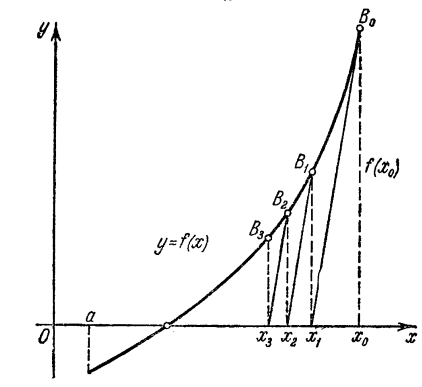
Рис. 6.5

Видоизмененный метод Ньютона избавляет нас от необходимости вычислять каждый раз значение производной , что весьма полезно, еслиявляется сложной.