
Kursovaya_rabota_programmirovanie
.pdfТаблица 3.1. Значения ti в формуле Чебышева
n |
i |
ti |
2 |
1; 2 |
0,577350 |
3 |
1; 3 |
0,707107 |
|
2 |
0 |
4 |
1; 4 |
0,794654 |
|
2; 3 |
0,187592 |
5 |
1; 5 |
0,832498 |
|
2; 4 |
0,374541 |
|
3 |
0 |
6 |
1; 6 |
0,866247 |
|
2; 5 |
0,422519 |
|
3; 4 |
0,266635 |
7 |
1; 7 |
0,883862 |
|
2; 6 |
0,529657 |
|
3; 5 |
0,323912 |
|
4 |
0 |
Квадратурные формулы Гаусса
Вернемся к общему виду квадратурной формулы для функции заданной на промежутке [–1; 1]
1 |
n |
|
f (t)dt Ai f (ti ) |
( 3.52) |
|
1 |
i 1 |
|
Попытаемся найти коэффициенты Ai и узловые точки ti, таким образом, чтобы квадратурная формула (3.48) была точной для всех полиномов f(t) степени 2n–1
f(t)=1, t, t2, … , t2n–1.
В этом случае построение квадратурной формулы вида (3.52) приводит к определению Ai и ti из нелинейной системы 2n уравнений:
n |
|
|
|
|
|
|
|
Ai |
2, |
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
n |
ti |
0, |
|
|
|
|
|
Ai |
|
|
|
|
|||
i 1 |
|
|
|
2 |
|
|
|
n |
2n 2 |
|
|
|
|
||
Ai |
ti |
|
|
|
|
, |
( 3.53) |
|
2n 1 |
||||||
i 1 |
|
|
|
|
|
||
............................... |
|
||||||
n |
|
|
|
|
|
|
|
Ai t2n 1 0,i 1 i
61
Решение нелинейной системы (3.53) задача нетривиальная, но ее можно обойти, если знать, что значениями ti квадратурной формулы (3.52) служат корни многочлена Лежандра Pn(t)
Pn |
(t) |
1 |
|
|
dn |
t2 1 2 , |
n 0,1,2... |
( 3.54) |
|
|
dtn |
||||||
|
2n n! |
|
|
|
|
|||
Как известно, корни полинома (3.54) существуют при любом n, различны и принадлежат интервалу [–1; 1].
Значения Ai вычисляют интегрированием базисных многочленов Лежандра Pi(t) степени n–1:
1 |
|
|
t t ... t t |
i 1 |
t |
t |
i 1 |
... t t |
n |
|
|
|
|
|||||||||||||||
Ai |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
||||||
t |
|
t ... t |
|
|
|
|
t |
|
|
|
|
... t |
|
t |
|
|
||||||||||||
1 |
i |
i |
t |
i 1 |
i |
t |
i |
1 |
i |
n |
|
|||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Итак, выражение (3.52) или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
b |
|
|
|
b a |
|
|
n |
|
|
|
|
a b |
|
|
b a |
|
|
|
|
|
||||||||
f (x)dx |
|
Ai |
f |
|
|
|
|
|
|
|
|
|
ti |
|
|
|||||||||||||
2 |
|
|
2 |
|
|
2 |
|
|
|
|||||||||||||||||||
a |
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
( 3.55)
( 3.56)
где ti – корни полинома (3.54), а Ai определяется из (3.55), называют квадратурной формулой Гаусса. Для удобства практического применения квадратурной формулы Гаусса значения ti и Ai, для n = 2, 3, 4, 5, приведены в табл. 3.2.
Таблица 3.2. Значения ti и Ai в формуле Гаусса |
|
||
n |
i |
ti |
Ai |
2 |
1; 2 |
0,577350 |
1 |
3 |
1; 3 |
0,707107 |
5 |
9 |
|||
|
2 |
0 |
8 |
|
|
|
9 |
4 |
1; 4 |
0,794654 |
0,347855 |
|
2; 3 |
0,187592 |
0,652145 |
5 |
1; 5 |
0,832498 |
0,236927 |
|
2; 4 |
0,374541 |
0,478629 |
|
3 |
0 |
0,568889 |
Метод Монте-Карло
Метод Монте-Карло – это статистический метод. Его используют при вычислении сложных интегралов, решении систем алгебраических уравнений высокого порядка.
Алгоритм вычисления интеграла методом Монте-Карло следующий. Для
b
вычисления определенного интеграла f (x)dx вводят случайную величину U,
a
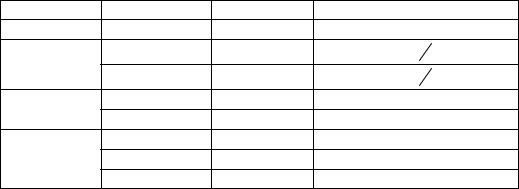
равномерно распределенную на отрезке интегрирования [a;b] (рис. 3.4). и
изменяющуюся по какому то правилу. Случайную величину выбирают таким
образом, чтобы искомая в задаче величина стала математическим ожидание от U.
62
Математическое ожидание случайной величины можно легко оценить, смоделировав эту случайную величину и посчитав выборочное среднее. Для этого бросаем N точек, равномерно распределённых на [a;b] (рис. 3.4) и для каждой точки Ui вычисляем значение f(Ui). Затем вычисляем выборочное среднее
|
1 |
N |
|
|
||
значение: |
f (Ui ). |
В этом случае интеграл считается по приближенной |
||||
|
||||||
формуле |
N i 1 |
|
|
|||
|
|
b a |
|
|||
b |
|
|
N |
|||
f (x)dx |
f (Ui ) |
|||||
|
||||||
a |
|
|
N |
|
i 1 |
|
Точность оценки зависит только от количества точек N.
Рисунок 3.4. Геометрическая интерпретация метода Монте-Карло
Геометрическая интерпретация – область интегрирования заполняется случайными точками, на каждой из которых строим «столбик», определяя его
ширину как b a . Далее суммируются площади «столбиков».
N
Для определения площади под графиком функции можно использовать следующий алгоритм:
ограничить функцию прямоугольником, площадь которого Sпр легко вычисляется;
«набросать» в этот прямоугольник N точек, координаты которых выбираются случайным образом;
определить К число точек, которые попадут под график функции;
площадь области, ограниченной функцией и осями координат, S
K
определяется выражением S Sпр N
Вычисление интеграла с заданной точностью
При одном и том же числе точек формула Симпсона в большинстве случаев намного точнее, чем формулы прямоугольников и трапеций.
Точность интегрирования по методу прямоугольников с постоянным шагом h связана с величиной шага следующим образом:
h.
63
При интегрировании методом трапеций это соотношение имеет вид:
h2.
Метод Симпсона обеспечивает точность вычислений
h2 h4.
Ошибка в выборе величины шага интегрирования либо не обеспечит нужной точности, либо приведет к необоснованным затратам машинного времени. Заданную точность при минимальных затратах времени обеспечивают алгоритмы интегрирования с автоматическим выбором величины шага.
Для достижения нужной точности поступают следующим способом:
1.Задаются начальным значением N и вычисляют интеграл S1 для принятого N.
2.Уменьшают N в два раза и вычисляют новое значение интеграла S2 для нового N.
3.Если разность |S2 - S1| меньше заданной точности , то интеграл вычислен. Если разность больше , то возвращаемся на п.2
3.3.Метод наименьших квадратов
Метод наименьших квадратов используется при обработке реальных количественных данных, полученных в результате всевозможных научных опытов, технических испытаний, астрономических, геодезических и т.п. наблюдений.
Пусть в результате эксперимента были получены некоторые данные, представленные в виде таблицы (табл. 3.3). Необходимо построить аналитическую зависимость, наиболее близко описывающую результаты эксперимента.
Таблица 3.3. Экспериментальные данные
xi |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
… |
xn |
yi |
y1 |
y2 |
y3 |
y4 |
y5 |
y6 |
y7 |
… |
yn |
Идея метода наименьших квадратов заключается в том, что функцию
Y = f(x, a0 a1, ..., ak)
необходимо подобрать таким образом, чтобы сумма квадратов отклонений измеренных значений yi от расчетных Yi была наименьшей (рис. 3.5):
n |
|
S yi f xi ,a0,a1,...,ak 2 min |
( 3.57) |
i 1
64

Рисунок 3.5. Геометрическая интерпретация метода наименьших квадратов
Задача сводится к определению коэффициентов ai из условия (3.57). Для ее решения необходимо составить систему уравнений
S |
|
|
|
|
|
|
0, |
||
a0 |
||||
|
|
|
||
S |
|
|
||
|
0, |
|||
a1 |
||||
|
|
|
||
..... |
|
|||
S |
|
|
|
|
|
0, |
|||
ak |
|
|||
|
|
|
||
Если параметры ai входят в зависимость Y = f(x, a0 a1, ..., ak) линейно, то получим систему из k-линейных уравнений с k неизвестными:
n |
|
|
|
|
|
|
|
2 |
|
S |
|
|
|
|
yi |
f xi ,a0 ,a1,...,ak |
|
|
|
0 |
|
|
|||||||
a0 |
|
|||||||||||||
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
y |
|
f x |
,a |
|
,a ,...,a |
|
2 |
S |
|
0 |
|
||
|
i |
0 |
k |
|
|
|||||||||
|
i |
|
1 |
|
|
a1 |
|
|
|
( 3.58) |
||||
i 1 |
|
|
|
........... |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
2 |
|
S |
|
|
|
|
yi |
f xi ,a0 ,a1,...,ak |
|
|
|
|
0 |
|
|||||||
|
ak |
|
|
|||||||||||
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Зная коэффициенты ai, являющиеся решением системы (3.58), можно составить искомую функцию Y = f(x, a0, a1, ..., ak).
Подбор параметров линейной функции
Пусть необходимо определить параметры функции: Y = a0 + a1x. Составим многочлен (3.57) для заданной функции:
n
Syi a0 a1xi 2
i 1
65
Сформируем систему линейных уравнений (3.58), решив которую, определим коэффициенты функции Y = a0 + a1x:
n |
|
|
|
|
|
|
2 |
|
|
S |
|
|
|
n |
|
|
|
|
|
|
|
|
|||
yi a0 |
a1xi |
|
|
|
|
|
|
0 |
|
2 yi |
a0 |
a1xi ( 1) 0 |
|
|
|||||||||||
|
|
a0 |
|
||||||||||||||||||||||
i 1 |
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|||||
n |
|
|
|
|
|
|
|
|
|
S |
|
|
|
n |
|
|
|
|
|
|
|
||||
|
y |
|
a |
|
a x 2 |
|
0 |
|
2 yi |
a0 a1xi ( xi ) 0 |
|
||||||||||||||
i |
0 |
|
|
|
|||||||||||||||||||||
|
|
|
1 |
i |
|
|
a1 |
|
|
|
i 1 |
|
|
|
|
|
|
|
|
||||||
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|||
|
a0 n a1 xi |
yi |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
i 1 |
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
n |
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|||||
a0 xi |
a1 xi2 yi xi |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
i 1 |
|
|
i 1 |
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
n |
|
|
|
n |
|
|
|
|
|
|
|
|
n |
|
|
|
n |
n |
|
|
|
|
a0 |
|
yi |
a1 |
xi |
a1 |
|
n yi xi |
yi xi |
|
|
|||||||||||||||
|
i 1 |
|
|
i 1 |
|
, |
|
|
|
i 1 |
|
|
i 1 |
i 1 |
|
. |
|
( 3.59) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||||
|
|
|
n |
|
|
|
n |
|
|
n |
2 |
|
|
n |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n xi |
|
xi |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
i 1 |
|
|
|
|
|
||
Квадратичная функция
Необходимо определить параметры функции: Y = a0 + a1 x + a2 x2. Составим функцию (3.57):
|
|
n |
|
2 |
2 |
|
|
S yi |
a0 a1xi |
||
|
|
a2 xi |
. |
||
|
|
i 1 |
|
|
|
После дифференцирования система уравнений (3.58) примет вид: |
|||||
|
n |
n |
n |
|
|
a0 n a1 xi |
a2 xi2 yi |
|
|||
|
i 1 |
i 1 |
i 1 |
|
|
n |
n |
n |
n |
|
|
a0 xi |
a1 xi2 a2 xi3 yi xi |
|
( 3.60) |
||
i 1 |
i 1 |
i 1 |
i 1 |
|
|
n |
n |
n |
n |
|
|
a0 xi2 a1 xi3 a2 xi4 yi xi2 |
|
||||
i 1 |
i 1 |
i 1 |
i 1 |
|
|
Решив систему (3.60), найдем значение параметров ao, a1, a2.
Кубическая функция
Необходимо определить параметры многочлена третьей степени:
Y = ao + a1 x + a2 x2 + a3 x3.
Составим функцию
n |
3 |
2 |
2 |
||
S yi a0 a1xi a2xi |
a3xi |
|
i 1 |
|
|
Система уравнений для вычисления параметров ao, a1, a2, a3 примет вид:
66
|
n |
n |
n |
n |
|
|
a0 n a1 xi a2 xi2 a3 xi3 yi |
|
|||||
|
i 1 |
i 1 |
i 1 |
i 1 |
|
|
n |
n |
n |
n |
n |
|
|
a0 xi |
a1 xi2 a2 xi3 a3 xi4 yixi |
|
|
|||
i 1 |
i 1 |
i 1 |
i 1 |
i 1 |
|
|
n |
n |
n |
n |
n |
|
( 3.61) |
a0 xi2 |
a1 xi3 |
a2 xi4 |
a3 xi5 |
yixi2 |
||
i 1 |
i 1 |
i 1 |
i 1 |
i 1 |
|
|
n |
n |
n |
n |
n |
|
|
3 |
4 |
5 |
6 |
3 |
|
|
a0 xi |
a1 xi |
a2 xi |
a3 xi |
yixi |
|
|
i 1 |
i 1 |
i 1 |
i 1 |
i 1 |
|
|
Полином k-й степени
Необходимо определить параметры многочлена k-й степени:
Y=a0 + a1x + a1x2 +... + ak xk.
Тогда система уравнений для определения параметров ak принимает вид:
|
n |
n |
|
n |
n |
a0 n |
a1 xi |
a2 xi2 |
|
... ak xik |
yi |
|
i 1 |
i 1 |
|
i 1 |
i 1 |
n |
n |
n |
|
n |
n |
a0 xi |
a1 xi2 |
a2 xi3 |
... |
ak xik 1 yixi |
|
i 1 |
i 1 |
i 1 |
|
i 1 |
i 1 |
...............................................................................
( 3.62)
n |
n |
n |
n |
n |
|
a0 xik a1 xik 1 |
a2 xik 2 |
... ak xi2k yi xik |
|||
i 1 |
i 1 |
i 1 |
i 1 |
i 1 |
|
Получив коэффициенты полинома, необходимо произвести выравнивание значений экспериментальной зависимости, то есть выполнить расчет теоретических значений по полученной формуле.
Функции, приводимые к линейной
Для вычисления параметров функции Y = axb необходимо выполнить некоторые арифметические преобразования:
ln(y) = ln(axb) = ln (a) + b ln (x)
и сделать замену
Y = ln (y), X = ln (x), A = ln (a),
которая приведет заданную функцию к линейному виду Y = A + bX, где коэффициенты A и b вычисляются по формулам (3.59) и, соответственно, a = eA.
Аналогично можно подобрать параметры функции вида Y = aebx. Прологарифмируем заданную функцию:
ln (y) = ln (a) + bx ln (e) ln (y) = ln (a) + bx.
Проведем замену:
Y = ln (y), A = ln (a)
и получим линейную зависимость Y = bx + A.
По формулам (3.59) найдем A и b, а затем вычислим a = eA.
Ниже, в табл. 3.4, приведены примеры еще нескольких функций, которые сводятся к линейной функции элементарными заменами.
67

Таблица 3.4. Преобразование функций Y = f(x, a,b) к виду Y = Ax + b
Функция |
Замена |
Функция |
Замена |
|
|
Функция |
|
Замена |
||||||||||||||
1 |
|
1 |
|
|
x |
|
Y |
1 |
;X |
1 |
|
|
|
1 |
|
|
|
1 |
x |
|||
y |
|
|
Y |
|
|
y |
|
y |
x |
|
y |
x |
b |
|
Y |
,X e |
||||||
ax b |
y |
|||||||||||||||||||||
|
|
|
ax b |
|
|
|
|
|
|
ae |
|
|
|
y |
|
|||||||
Подбор параметров функции y = axbecx
Прологарифмируем выражение Y = axbecx:
ln (y)= ln (a) + b ln (x) + cx ln (e)
и сделаем замену Y = ln (y), A = ln (a):
Y = A + b ln (x) + cx.
Составим функцию по формуле (3.57):
n
S(A,b,c) yi A bln(xi ) cxi 2 .
i 1
После дифференцирования получим систему трех линейных алгебраических уравнений для определения коэффициентов A, b и c.
|
n |
|
n |
|
|
n |
|
|
|
A n b ln(xi ) c xi |
yi |
|
|
||||||
|
|
|
|||||||
|
i 1 |
|
i 1 |
|
|
i 1 |
|
|
|
n |
n |
) 2 |
n |
|
|
n |
|
|
|
A ln(xi ) b ln(xi |
c xi |
ln(xi ) yi |
ln(xi |
) |
( 3.63) |
||||
i 1 |
i 1 |
|
i 1 |
|
|
i 1 |
|
|
|
n |
n |
|
n |
|
|
n |
|
|
|
A xi |
b xi |
ln(xi ) c xi2 |
yi xi |
|
|
|
|||
i 1 |
i 1 |
|
i 1 |
|
|
i 1 |
|
|
|
Значение коэффициента а вычислим по формуле a = еA.
Уравнение регрессии и коэффициент корреляции
Линия, описываемая уравнением вида y = a0 + a1x, называется линией регрессии y на x, параметры a0 и a1 называются коэффициентами регрессии и
определяются формулами (3.59).
n |
|
a0 2 |
|
Чем меньше величина S yi |
a1xi |
тем более обоснованно |
|
i 1 |
|
|
|
предположение, что экспериментальные данные описываются линейной функцией. Существует показатель, характеризующий тесноту линейной связи между x и y, называемый коэффициентом корреляции и рассчитываемый по формуле:
|
|
n |
Mx yi My |
|
|
n |
|
|
n |
|
|||||
r |
|
xi |
Mx |
|
xi |
My |
|
yi |
|
||||||
|
i 1 |
|
|
|
, |
|
i 1 |
, |
|
i 1 |
, |
( 3.64) |
|||
|
|
|
|
|
|
|
|||||||||
xi Mx |
|
||||||||||||||
|
|
2 yi My 2 |
|
|
n |
|
|
n |
|
||||||
|
|
n |
|
n |
|
|
|
|
|
|
|
|
|
||
|
|
i 1 |
|
i 1 |
|
|
|
|
|
|
|
|
|
||
Значение коэффициента корреляции удовлетворяет соотношению: –1 r 1.
68

Чем меньше отличается абсолютная величина r от единицы, тем ближе к линии регрессии располагаются экспериментальные точки.
Если коэффициент корреляции равен нулю, то это означает, что между x и y не существует линейной связи, но между ними может существовать зависимость, отличная от линейной.
Криволинейная корреляция
Обычно коэффициент корреляции r применяется только в тех случаях, когда между данными существует прямолинейная связь. Если же связь криволинейная, то пользуются индексом корреляции, который рассчитывается по формуле:
|
|
n |
|
|
R |
1 |
yi Yi 2 |
||
i 1 |
|
( 3.65) |
||
n |
|
|||
|
|
yi |
My 2 |
|
|
|
i 1 |
|
|
где y – экспериментальные значения, Y – теоретические значения,
My – среднее значение y.
Индекс корреляции по своему абсолютному значению колеблется в пределах от 0 до 1. При функциональной зависимости индекс корреляции равен 1. При отсутствии связи R = 0. Если коэффициент корреляции r является мерой тесноты связи только для линейной формы связи, то индекс корреляции R – и для линейной, и для криволинейной. При прямолинейной связи коэффициент
корреляции по своей абсолютной величине равен индексу корреляции: r R.
3.4. Интерполяция функций
Простейшая задача интерполирования заключается в следующем. На отрезке [a,b] заданы n+1 точки x0, x1, x2, …, xn, которые называют узлами интерполяции, и значения некоторой функции f(x) в этих точках
f(x0) y0, f(x1) y1, f(x2) y2,...,f(xn ) yn |
( 3.66) |
Требуется построить интерполирующую функцию F(x), принадлежащую известному классу и принимающую в узлах интерполяции те же значения, что и f(x), т.е. такую, что
F(x0 ) y0,F(x1) y1,F(x2 ) y2,...,F(xn ) yn |
( 3.67) |
Геометрически (рис. 3.6) это означает, что нужно найти кривую y=F(x), некоторого определенного типа, проходящую через заданную систему точек
Mi(xi,yi) (i=0, 1, 2 .. n).
В такой общей постановке задача может иметь бесчисленное множество решений или совсем не иметь решений. Однако эта задача становится однозначной, если вместо произвольной функции F(x) искать полином Pn(x) степени не выше n, удовлетворяющей условиям (3.66), т.е. такой, что
Pn(x0) y0,Pn(x1) y1,Pn(x2) y2,...,Pn(xn) yn .
69
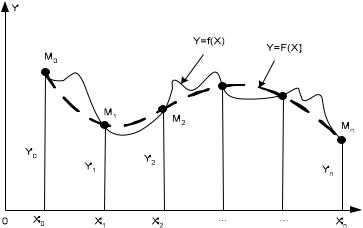
Рисунок 3.6. Геометрическая интерпретация интерполирования
Полученную интерполяционную формулу y=F(x), обычно используют для приближенного вычисления значений данной функции f(x) для значений аргумента x, отличных от узлов интерполирования. Такая операция называется
интерполированием функции f(x). При этом различают интерполирование в узком смысле, когда X [x0,xn], и экстраполирование, когда X [x0,xn].
Рассмотрим некоторые, наиболее часто используемые интерполяционные полиномы.
Канонический полином
Будем искать интерполирующую функцию F(x) в виде многочлена степени n.
( 3.68)
Выбор многочлена степени n основан на том факте, что через n+1 точку проходит единственная кривая степени n.
Подставив (3.66) в (3.67), получим систему линейных алгебраических уравнений:
|
n |
n 1 |
n 2 |
|
an 1x0 an y0 |
|||
a0x0 |
a1x0 |
a2x0 |
||||||
|
|
a xn 1 |
a xn 2 |
|
a |
x a |
y |
|
a xn |
||||||||
|
0 1 |
1 1 |
2 0 |
|
|
n 1 1 |
n |
1 |
.......... |
|
|
.................... |
.................... |
|
......... |
|
|
( 3.69) |
|
|
|
a xn 1 |
a xn 2 |
|
a |
x a |
y |
|
a xn |
n |
||||||||
|
0 |
n |
1 n |
2 0 |
|
n 1 |
n n |
|
|
Решая эту систему относительно переменных a0, a1, ..., an, найдем аналитическое выражение интерполяционного полинома (3.68).
Итак, пусть функция f(x) задана на отрезке [x0,xn] точками x0, x1, x2, …, xn, в которых она принимает значения y0, y1, y2, …, yn. Необходимо вычислить значение этой функции в некоторой точке T [x0,xn], используя интерполяционный канонический полином.
70
