Kursovaya_rabota_programmirovanie

Тогда, согласно идее метода Зейделя, предполагая, что к–е приближения корней известны, будем строить (к+1)–е приближения по следующим формулам:

xik 1 i ij xkj 1 ij xkj ;

j 1 j i

...............................................

Возникает вопрос о сходимости метода. Необходимо перейти к системе x x таким образом, чтобы выполнялись все условия сходимости. Выполним следующие преобразования:

эквивалентна системе A x=b и обладает следующими свойствами:

матрица F – симметрична, т.е. fij=fji;

все элементы главной диагонали матрицы F положительны fii>0;

соответствующая квадратичная форма является положительно определенной.

Теперь, если систему (3.21) привести к специальному виду

то она будет сходиться к единственному решению при любом начальном приближении.

Метод скорейшего спуска (метод градиента)

Довольно распространенным итерационным методом решения линейных систем является метод градиента или, как его еще называют, метод скорейшего спуска. Рассмотрим систему линейных уравнений

51

...................................

n

fn anj xj bn 0

j 1

сдействительной матрицей A={aij} и столбцом свободных коэффициентов b={bi}.

Алгоритм градиентного метода для решения линейных систем:

1)Выбираем начальное приближение, например x=b.

2)Вычисляем невязку r по формуле (3.26).

3)Находим расчетный коэффициент по формуле (3.27). Здесь под выражениями в скобках понимаются скалярные произведения соответствующих векторов.

4)Определяем x по формуле (3.25).

5)Если максимальная невязка системы не превышает точность вычислений , то решение x найдено, иначе переходим к п.2.

Метод релаксации

Метод релаксации или иначе, метод ослабления, это еще один итерационный способ решения линейных систем.

Пусть дана линейная система (3.1). Подготовим ее к релаксации. Для этого перенесем свободные члены налево и разделим первое уравнение на (–а11), второе на (–а22), и т.д. Получим систему вида

52

Пусть задан вектор начальных приближений x0. Подставим его в (3.28) и получим невязки:

Если одной из неизвестных xk0 дать приращение xk0, то соответствующая невязка Rk0 уменьшиться на величину xk0, а все остальные невязки Ri0 (i k) увеличатся на величину bik xk0. Таким образом, чтобы обратить очередную невязку Rk1 в нуль, достаточно величине xk0 дать приращение xk0 = Rk0, и мы будем иметь Rk1=0 и

Идея метода релаксации заключается в том, что на каждом шаге обращается в нуль максимальная по модулю невязка путем изменения значения соответствующей компоненты приближения. Процесс заканчивается, когда все невязки последней преобразованной системы будут равны нулю с заданной точность.

Алгоритм решение линейной системы методом релаксации:

1) Подготовка системы к релаксации, то есть ее преобразование по формулам (3.29).

2)Формирование вектора начальных приближений x0=0.

3)Расчет первых невязок R1 по (3.30).

4)Определения текущего вектора невязок R0.

5)Вычисление максимальной невязки системы (или иначе приращения ) и ее номера.

6)Уточнение невязки R1 в соответствии с формулой (3.31).

7)Вычисление значения корня Х с номером, соответствующим номеру максимальной невязки, как суммы приращения .

8)Если хотя бы одна невязка системы не равна нулю с заданной точность , то перейти к п.4, иначе решение системы Х найдено.

53

3.2. Методы численного интегрирования

Пусть дана функция f(x), известно, что она непрерывна на интервале [a, b] и уже определена ее первообразная F(x), тогда определенный интеграл от этой функции можно вычислить в пределах от a до b по формуле Ньютона–Лейбница:

a

f (x)dx F(b) F(a),

где F (x)= f(x).

Однако на практике часто встречаются интегралы c первообразной, которая не может быть выражена через элементарные функции или является слишком сложной, что затрудняет, или делает невозможным, вычисления по формуле (3.32). Кроме того, нередко подынтегральная функция задается таблицей или графиком и тогда понятие первообразной вообще теряет смысл. В этом случае, большое значение имеют численные методы интегрирования, основная задача которых заключается в вычислении значения определенного интеграла на основании значений подынтегральной функции.

Численное вычисление определенного интеграла называют механической квадратурой. Формулы, соответствующие тому или иному численному методу приближенного интегрирования называют квадратурными. Подобное название связано с геометрическим смыслом определенного интеграла: значение определенного интеграла

b

равно площади квадрата, которая в свою очередь, совпадает с площадью криволинейной трапеции с основаниями [a, b] и f(x).

Интегрирование по методу трапеций

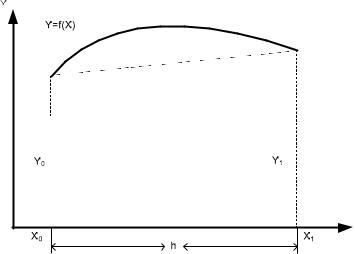
Для интегрирования методом трапеций участок интегрирования [a; b] также разбивают на n равных частей. Если провести ординаты во всех точках деления и заменить каждую из полученных криволинейных трапеций прямолинейной (рис. 3.1), то приближенное значение интеграла будет равно сумме площадей прямолинейных трапеций.

Площадь отдельной трапеции составляет:

S yi 1 yi h,

2

следовательно, площадь искомой фигуры вычисляют по формуле:

54

Суммируя площади всех криволинейных трапеций, получим:

где p = 6 – p, p = 4.

Следовательно, формула Симпсона для численного интегрирования имеет

вид:

Квадратурные формулы Ньютона–Котеса

Пусть необходимо вычислить интеграл для функции y=f(x)

a

ydx

b

Выберем шаг h=(b–a)/n и разобьем отрезок [a; b] на n равных частей, так что x0=a, xi = x0 + ih i = 1, …, n–1, xn=b, и пусть yi=f(xi) для i = 0, 1, …, n.

Заменим функцию y соответствующим полиномом Лагранжа и получим приближенную квадратурную формулу

Для того чтобы использовать выражение (3.39) вместо y нужно изменить границы интегрирования. Значению x=a будет соответствовать q=0, а значению x=b – q=n. Так же необходимо учесть, что dx=h dq. Таким образом, имеем

56

постоянные, которые называют коэффициентами Котеса.

Квадратурная формула Ньютона–Котеса при этом имеет вид

Применим формулы (3.42) и (3.43) для n=1. Имеем

Таким образом, получили уже известную формулу трапеций (рис. 3.3) для вычисления определенного интеграла.

Рисунок 3.3. Геометрическая интерпретация формулы Ньютона–Котеса для n=1.

57

Положим n=2 и подставим в (3.42) и (3.43):

Следовательно, так как x2–x0=2 h, имеем формулу Симпсона

Формулы Ньютона–Котеса определяют семейство квадратурных формул, параметром которого является число n – степень интерполяционного многочлена, которым заменяется подынтегральная функция.

Для n>2 получают квадратурные формулы Ньютона–Котеса высших порядков. Проведем вычисления, например, для n=3. Из формул (3.42) и (3.43) получим

Эта формула носит название квадратурной формулы Ньютона или правила трех восьмых.

Коэффициенты Котеса при большом числе ординат вычислить не так просто. Поэтому на практике для приближенного вычисления определенных интегралов поступают так. Разбивают промежуток интегрирования на достаточно большое число маленьких отрезков и к каждому из них применяют квадратурную формулу Ньютона–Котеса с небольшим числом ординат. В результате получаются не сложные формулы и расчеты по ним дают достаточно высокую точность.

Будем считать, что задан интервал интегрирования [a; b], определена подынтегральная функции f(x), сформирована по формуле (3.42) матрица Н коэффициентов Котеса, известно число разбиений интервала n и порядок N квадратурной формулы Ньютона–Котеса. Приведем алгоритм вычисления значения определенного интеграла по формулам Ньютона–Котеса.

1.Определить шаг h=(b–a)/n разбиения отрезка [a; b].

2.Сформировать массив Х, соответствующий абсциссам точек разбиения отрезка.

3.Начать процесс вычисления значения определенного интеграла, положив

Sum=0.

4.Организовать цикл параметр, которого i будет изменяться от 0 до n–1 и и характеризовать i–е разбиение интервала [a; b] на более мелкие отрезки. В цикле необходимо выполнить следующее.

5.Определить шаг dh разбиения отрезка [Xi+1; Xi].

58

6.Сформировать массив значений x точек разбиения отрезка [Xi+1; Xi].

7.Вычислить значения подынтегральной функции в этих точках, сформировав массив y.

8.Выполнить расчет коэффициентов А по формуле (3.41).

9.Определить значение определенного интеграла S на интервале [Xi+1; Xi] по формуле (3.43).

10. Добавить найденное значение S к общей сумме Sum и перейти к п. 5. Значение интеграла Sum будет найдено, когда будут определены и

Квадратурные формулы Чебышева

Напомним общую квадратурную формулу, выведенную ранее

b n

ydx Ai f (xi )

a i 0

Во всех рассмотренных квадратурных формулах xi располагались на равном расстоянии h. В формулах, предложенных Чебышевым, квадратурные коэффициенты рассчитываются специальным образом.

Сделаем линейную замену

22

ипреобразуем исходный интеграл к интегралу с промежутком интегрирования [–1;1]:

Следует обратить внимание, что в (3.46) n – это число узлов интегрирования ti, а не число разбиений отрезка [a; b], как это было в квадратурных формулах Ньютона–Котеса. Причем ti выбирают таким образом, чтобы

коэффициенты Bi были равны между собой:

квадратурная формула (3.46) была точной для всех полиномов до степени n включительно

f(t) 1. ( 3.48)

59

Заметим, что формула (3.49), согласно условию (3.48) должна быть точной для функций вида

f(t)=t, t2, … , tn.

Подставляя эти функции в (3.48), получим систему уравнений, из которой могут быть определены неизвестные ti (i=1, 2, …, n):

Доказано, что система (3.51) имеет единственный набор решений ti при i=1, 2, 3, 4, 5, 6, 7, 9 и не имеет действительных решений при i=8 и i 10. В таблице 3.1 приведены значения корней ti системы (3.51) для n=2..7.

Итак, если заданы пределы интегрирования a и b, известно число n и определены коэффициенты Чебышева t, то алгоритм решения определенного интеграла, с помощью квадратурных формул Чебышева будет выглядеть так:

1. Формирование массива абсцисс

2.Расчет значений функции yi=F(xi).

3.Вычисление значение определенного интеграла, как суммы yi.

60