
- •ВВЕДЕНИЕ
- •1. ОБЩАЯ ХАРАКТЕРИСТИКА НЕФТЯНОЙ ЗАЛЕЖИ
- •1.1. Понятие о нефтяной залежи
- •1.2. Механизм использования пластовой энергии при добыче нефти
- •2. ИСТОЧНИКИ ПЛАСТОВОЙ ЭНЕРГИИ
- •2.1. Пластовые давления
- •2.1.1. Статическое давление на забое скважины
- •2.1.2. Статический уровень
- •2.1.3. Динамическое давление на забое скважины
- •2.1.4. Динамический уровень жидкости
- •2.1.5. Среднее пластовое давление
- •2.1.6. Пластовое давление в зоне нагнетания
- •2.1.7. Пластовое давление в зоне отбора
- •2.1.8. Начальное пластовое давление
- •2.1.9. Текущее пластовое давление
- •2.1.10. Приведенное давление
- •2.2. Приток жидкости к скважине
- •2.3. Режимы разработки нефтяных месторождений
- •2.4. Водонапорный режим
- •2.5. Упругий режим
- •2.6. Режим газовой шапки
- •2.7. Режим растворенного газа
- •2.8. Гравитационный режим
- •3. ТЕХНОЛОГИЯ И ТЕХНИКА ВОЗДЕЙСТВИЯ НА ЗАЛЕЖЬ НЕФТИ
- •3.1. Цели и методы воздействия
- •3.2. Технология поддержания пластового давления закачкой воды
- •3.2.1. Размещение скважин
- •3.3. Основные характеристики поддержания пластового давления закачкой воды
- •3.4. Водоснабжение систем ППД
- •3.5. Техника поддержания давления закачкой воды
- •3.5.1. Водозаборы
- •3.5.2. Насосные станции первого подъема
- •3.5.3. Буферные емкости
- •3.5.4.Станции второго подъема
- •3.6. Оборудование кустовых насосных станций
- •3.7. Технология и техника использования глубинных вод для ППД
- •3.8. Поддержание пластового давления закачкой газа
- •3.9. Методы теплового воздействия на пласт
- •3.10. Техника закачки теплоносителя в пласт
- •3.11. Внутрипластовое горение
- •4. ПОДГОТОВКА СКВАЖИН К ЭКСПЛУАТАЦИИ
- •4.1. Конструкция оборудования забоев скважин
- •4.2. Приток жидкости к перфорированной скважине
- •4.3. Техника перфорации скважин
- •4.4. Пескоструйная перфорация
- •4.5. Методы освоения нефтяных скважин
- •4.6. Передвижные компрессорные установки
- •4.7. Освоение нагнетательных скважин
- •5. МЕТОДЫ ВОЗДЕЙСТВИЯ НА ПРИЗАБОЙНУЮ ЗОНУ СКВАЖИНЫ
- •5.1. Назначение методов и их общая характеристика
- •5.2. Обработка скважин соляной кислотой
- •5.3. Термокислотные обработки
- •5.4. Поинтервальная или ступенчатая СКО
- •5.5. Кислотные обработки терригенных коллекторов
- •5.6. Техника и технология кислотных обработок скважин
- •5.7. Гидравлический разрыв пласта
- •5.8. Осуществление гидравлического разрыва
- •5.9. Техника для гидроразрыва пласта
- •5.10. Тепловая обработка призабойной зоны скважины
- •5.11. Термогазохимическое воздействие на призабойную зону скважины
- •5.12. Другие методы воздействия на призабойную зону скважин
- •6. ИССЛЕДОВАНИЕ СКВАЖИН
- •6.1. Назначение и методы исследования скважин
- •6.2. Исследование скважин при установившихся режимах
- •6.3. Исследование скважин при неустановившихся режимах
- •6.4. Термодинамические исследования скважин
- •6.5. Скважинные дебитометрические исследования
- •6.6. Техника и приборы для гидродинамических исследований скважин
- •7. ОСНОВЫ ТЕОРИИ ПОДЪЕМА ЖИДКОСТИ В СКВАЖИНЕ
- •7.1. Физика процесса движения газожидкостной смеси в вертикальной трубе
- •7.1.1. Зависимость подачи жидкости от расхода газа
- •7.1.2. Зависимость положения кривых q (V) от погружения
- •7.1.3. Зависимость положения кривых q(V) от диаметра трубы
- •7.1.4. К. п. д. процесса движения ГЖС
- •7.1.5. Понятие об удельном расходе газа
- •7.1.6. Зависимость оптимальной и максимальной подач от относительного погружения
- •7.1.7. Структура потока ГЖС в вертикальной трубе
- •7.2. Уравнение баланса давлений
- •7.3. Плотность газожидкостной смеси
- •7.4. Формулы перехода
- •8. ЭКСПЛУАТАЦИЯ ФОНТАННЫХ СКВАЖИН
- •8.1. Артезианское фонтанирование
- •8. 2. Фонтанирование за счет энергии газа
- •8. 3. Условие фонтанирования
- •8. 4. Расчет фонтанного подъемника
- •8. 5. Расчет процесса фонтанирования с помощью кривых распределения давления
- •8. 6. Оборудование фонтанных скважин
- •8.6.1. Колонная головка
- •8.6.2. Фонтанная арматура
- •8.6.3. Штуцеры.
- •8.6.4. Манифольды
- •8. 7. Регулирование работы фонтанных скважин
- •8. 8. Осложнения в работе фонтанных скважин и их предупреждение
- •8.8.1. Открытое фонтанирование
- •8.8.2. Предупреждение отложений парафина
- •8.8.3. Борьба с песчаными пробками
- •8.8.4. Отложение солей
- •9. ГАЗЛИФТНАЯ ЭКСПЛУАТАЦИЯ СКВАЖИН
- •9.1. Общие принципы газлифтной эксплуатации
- •9.2. Конструкции газлифтных подъемников
- •9.3. Пуск газлифтной скважины в эксплуатацию (пусковое давление)
- •9.4. Методы снижения пусковых давлений
- •9.4.1. Применение специальных пусковых компрессоров
- •9.4.2. Последовательный допуск труб
- •9.4.3. Переключение работы подъемника с кольцевой системы на центральную
- •9.4.4. Задавка жидкости в пласт
- •9.4.5. Применение пусковых отверстий
- •9.5. Газлифтные клапаны
- •9.6. Принципы размещения клапанов
- •9.7. Принципы расчета режима работы газлифта
- •9.8. Оборудование газлифтных скважин
- •9.9. Системы газоснабжения и газораспределения
- •9.10. Периодический газлифт
- •9.11. Исследование газлифтных скважин
- •10. ЭКСПЛУАТАЦИЯ СКВАЖИН ШТАНГОВЫМИ НАСОСАМИ
- •10.2. Подача штангового скважинного насоса и коэффициент подачи
- •10.3. Факторы, снижающие подачу ШСН
- •10.3.1. Влияние газа
- •10.3.2. Влияние потери хода плунжера
- •10.3.3. Влияние утечек
- •10.3.4. Влияние усадки жидкости
- •10.3.5. Нагрузки, действующие на штанги, и их влияние на ход плунжера
- •10.4. Оборудование штанговых насосных скважин
- •10.4.1. Штанговые скважинные насосы
- •10.4.2. Штанги
- •10.4.3. Насосные трубы
- •10.4.4. Оборудование устья скважины
- •10.4.5. Канатная подвеска
- •10.4.6. Штанговращатель
- •10.4.7. Станки-качалки (СК)
- •10.5. Исследование скважин, оборудованных штанговыми насосными установками
- •10.5.1. Эхолот
- •10.5.2. Динамометрия ШСНУ
- •10.5.3. Динамограмма и ее интерпретация
- •10.6. Эксплуатация скважин штанговыми насосами в осложненных условиях
- •11. ЭКСПЛУАТАЦИЯ СКВАЖИН ПОГРУЖНЫМИ ЦЕНТРОБЕЖНЫМИ ЭЛЕКТРОНАСОСАМИ
- •11.1. Общая схема установки погружного центробежного электронасоса
- •11.2. Погружной насосный агрегат
- •11.3. Элементы электрооборудования установки
- •11.4. Установка ПЦЭН специального назначения
- •11.5. Определение глубины подвески ПЦЭН
- •11.6. Определение глубины подвески ПЦЭН c помощью кривых распределения давления
- •12. ГИДРОПОРШНЕВЫЕ НАСОСЫ
- •12.1. Принцип действия гидропоршневого насоса
- •12.2. Подача ГПН и рабочее давление
- •13. ПОГРУЖНЫЕ ВИНТОВЫЕ НАСОСЫ
- •14. РАЗДЕЛЬНАЯ ЭКСПЛУАТАЦИЯ ПЛАСТОВ ОДНОЙ СКВАЖИНОЙ
- •14.1. Общие принципы
- •14.2. Некоторые схемы оборудования скважин для раздельной эксплуатации пластов
- •14.3. Раздельная закачка воды в два пласта через одну скважину
- •15. РЕМОНТ СКВАЖИН
- •15.1. Общие положения
- •15.2. Подъемные сооружения и механизмы для ремонта скважин
- •15.3. Технология текущего ремонта скважин
- •15.4. Капитальный ремонт скважин
- •15.5. Новая технология ремонтных работ на скважинах
- •15.6. Ликвидация скважин
- •16. ЭКСПЛУАТАЦИЯ ГАЗОВЫХ СКВАЖИН
- •16.1. Особенности конструкций газовых скважин
- •16.2. Оборудование устья газовой скважины
- •16.3. Подземное оборудование ствола газовых скважин при добыче природного газа различного состава
- •16.4. Оборудование забоя газовых скважин
- •16.5. Расчет внутреннего диаметра и глубины спуска колонны НКТ в скважину
- •16.5.1. Определение внутреннего диаметра колонны НКТ
- •16.5.2. Определение глубины спуска колонны НКТ в скважину
- •16.6. Способы и оборудование для удаления жидкости с забоя газовых и газоконденсатных скважин
- •16.7. Одновременная раздельная эксплуатация двух газовых пластов одной скважиной
- •СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
ЗКСПЛУАТАЦИЯ НЕФТЯНЫХ И ГАЗОВЫХ СКВАЖИН
7. ОСНОВЫ ТЕОРИИ ПОДЪЕМА ЖИДКОСТИ В СКВАЖИНЕ
Подъем жидкости из скважин нефтяных месторождений практически всегда сопровождается выделением газа. Поэтому для понимания процессов подъема жидкости из скважин, умения проектировать установки для подъема и выбирать необходимое оборудование, надо знать законы движения газожидкостных смесей (ГЖС) в трубах. При всех известных способах добычи нефти приходится иметь дело с движением газожидкостных смесей либо на всем пути от забоя до устья, либо на большей части этого пути. Эти законы сложнее законов движения однородных жидкостей в трубах и изучены хуже. Если при движении однофазного потока приходится иметь дело с одним опытным коэффициентом λ (коэффициент трения), то при движении двухфазного потока - газожидкостных смесей приходится прибегать по меньшей мере к двум опытным характеристикам потока, которые в свою очередь зависят от многих других параметров процесса и условий движения, многообразие которых чрезвычайно велико.
7.1. Физика процесса движения газожидкостной смеси в вертикальной трубе
7.1.1. Зависимость подачи жидкости от расхода газа
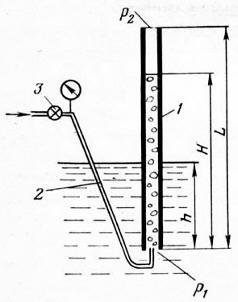
Качественную характеристику процесса движения газожидкостной смеси (ГЖС) в вертикальной трубе легче уяснить из следующего простого опыта (рис. 7.1). Представим, что трубка 1 длиною L погружена под уровень жидкости неограниченного водоема на глубину h. К нижнему открытому концу трубки, который по аналогии с промысловой терминологией будем называть башмаком, подведена другая трубка 2 для подачи с поверхности сжатого газа. На трубке имеется регулятор расхода 3, с помощью которого можно установить желаемый расход газа.
Рис. 7.1. Принципиальная схема газожидкостного подъемника
Давление у башмака подъемной трубки 1 будет равно гидростатическому на глубине h - P1 = gh и, очевидно, не будет изменяться от того, много или мало газа подается к башмаку. По трубке 2 подается газ,
и в трубке 1 создается газожидкостная смесь средней плотности с, которая поднимается на некоторую
180

ЗКСПЛУАТАЦИЯ НЕФТЯНЫХ И ГАЗОВЫХ СКВАЖИН
высоту H. Поскольку внутренняя полость трубки 1 и наружная область являются сообщающимися сосудами, имеющими на уровне башмака одинаковые давления, то можно написать равенство
g h с g H
откуда
H h . (7.1)
с
Плотность смеси в трубке с зависит от расхода газа V. Чем больше V, тем меньше с. Изменяя V, можно регулировать Н. При некотором расходе V = V1 величина Н может достигнуть L. При V<V1 H<L. При V>V1 H>L и наступит перелив жидкости через верхний конец трубки 1. При дальнейшем увеличении V расход поступающей на поверхность жидкости q увеличится. Однако при непрерывном увеличении V расход жидкости не будет увеличиваться непрерывно, так как под воздействием неизменяющегося перепада давления Р = Р1 - Р2 (Р1 = const, так как h = const), труба определенной длины L и диаметра d должна пропускать конечное количество жидкости, газа или газожидкостной смеси. Таким образом, при некотором расходе газа V=V2 дебит достигнет максимума q = q max.
Можно представить другой крайний случай, когда к башмаку подъемной трубы подводится так много газа, что при постоянном перепаде давления Р = Р1 - Р будет идти только газ, Р будет расходоваться на преодоление всех сопротивлений, вызванных движением по трубе чистого газа. Расход этого газа пусть будет V=V3. Если к башмаку подать еще больший расход (V>V3), то излишек газа не сможет пройти через подъемную трубу, так как ее пропускная способность при данных условиях (L, d, P) равна только V3, и устремится мимо трубы, оттесняя от башмака жидкость. Очевидно, при этом расход жидкости будет равен нулю (q = 0). Таким образом, из этого опыта можно сделать следующий вывод.
1. |
При V<V1 |
q = 0 |
(H < L). |
2. |
При V = V1 |
q = 0 |
(H = L) (начало подачи). |
3. V1 < V < V2 |
0 < q < qmax (H > L), |
||
4. |
При V = V2 |
q = qmax (точка максимальной подачи). |
|
5. |
При V2 < V < V 3 |
qmax > q > 0. |
|
6. |
При V = V3 |
q = 0 (точка срыва подачи). |
|
Обычно правая ветвь кривой q(V) (рис. 7.2) пологая, левая крутая.
Рис. 7.2. Зависимость подачи q газожидкостного подъемника от расхода газа V
181
ЗКСПЛУАТАЦИЯ НЕФТЯНЫХ И ГАЗОВЫХ СКВАЖИН
Для всех точек кривой постоянным является давление P1, так как погружение h в процессе опыта не изменялось. Существует понятие - относительное погружение = h / L. Таким образом, для данной кривой
еепараметром будет величина относительного погружения ε.
7.1.2.Зависимость положения кривых q (V) от погружения
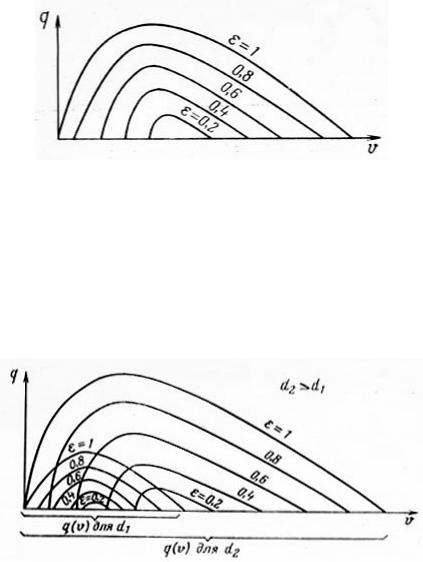
Поскольку при наших рассуждениях никаких ограничений на величину не накладывалось, то при любых , лежащих в пределах 0 < < 1, вид соответствующих кривых q(V) будет одинаковый. При увеличении е новые кривые q(V) обогнут прежнюю, так как с ростом h потребуется меньший расход газа для наступления перелива. По тем же причинам возрастет qmax, а точка срыва подачи на соответствующих кривых сместится вправо. При уменьшении все произойдет наоборот. Новые кривые q(V) расположатся внутри прежних и при = 0 кривая q(V) выродится в точку. Другой предельный случай - = 1 ( h = L, 100% погружения). В этом случае при бесконечно малом расходе газа немедленно произойдет перелив. Точка начала подачи сместится в начало координат. Кривая q(V) для = 1 начнется в начале координат и обогнет все семейство кривых. Таким образом, каждый газожидкостный подъемник характеризуется семейством кривых q(V), каждая из которых будет иметь свой параметр (рис. 7.3).
Рис. 7.3. Семейство кривых q(V) для газожидкостного подъемника данного диаметра
7.1.3.Зависимость положения кривых q(V) от диаметра трубы
Внаших рассуждениях никаких ограничений на диаметр подъемной трубы и на ее длину не
накладывается. Поэтому аналогичное семейство кривых q(V) должно существовать для подъемников любого диаметра и любой длины. Однако возникает вопрос, как располагать повое семейство кривых для трубы диаметром d2 > d1 по отношению к прежним кривым. Увеличение диаметра потребует большого расхода газа, так как
182

ЗКСПЛУАТАЦИЯ НЕФТЯНЫХ И ГАЗОВЫХ СКВАЖИН
Рис. 7.4. Семейство кривых q(V) для двух газожидкостных подъемников различных диаметров
объем жидкости, который необходимо разгазировать для достижения данной величины с, при прочих равных условиях ( h = const, L = const) возрастает пропорционально d2. Пропускная способность трубы по жидкости, газу или газожидкостной смеси (ГЖС) также возрастет. Поэтому для увеличенного диаметра будет существовать также семейство кривых q(V), все точки которого будут смещены вправо, в
сторону увеличенных объемов, кроме одной точки, совпадающей с началом координат для кривой q(V) при
= 1. В каждом из этих семейств и любых других, кривые q(V) при значениях , близких к единице и к нулю, не имеют практического значения, так как они либо неосуществимы ( = 0), либо бессмысленны ( = 1), и введены в рассуждения только для понимания физики процессов, происходящих при движении ГЖС в трубах.
7.1.4. К. п. д. процесса движения ГЖС
На каждой кривой q(V) имеется еще одна характерная и очень важная точка, точка так называемой оптимальной производительности, соответствующая наибольшему к. п. д. Если проанализировать произвольную кривую q(V), для которой = const, то для нее будут справедливы следующие рассуждения.
Из определения понятия к. п. д. следует, что
|
полезнаяработа |
|
Wп . |
(7.2) |
|
затраченнаяработа |
|||||
|
|
W |
|
||
|
|
|
з |
|
Полезная работа заключается в поднятии жидкости с расходом q на высоту L - h, так что
Wп q g L h . (7.3)
Затраченная работа - это работа газа, расход которого, приведенный к стандартным условиям, равен V. Полагая для простоты, что процесс расширения газа изотермический, на основании законов термодинамики идеальных газов можем записать
W |
V Рз0 |
Ln |
Р1 |
Р0 |
, |
(7.4) |
Р2 |
|
|||||
|
|
|
Р0 |
|
||
где Р1 + Рo - абсолютное давление у башмака; Р2 + Ро - то же на устье, Ро - атмосферное давление. Подставляя (7.3) и (7.4) в (7.2), получим
q g L h
V Р0 Ln Р1 Р0 .
Р2 Р0
В(7.5) все величины, кроме q и V, постоянны, которой ε = const. Следовательно, для данной кривой
(7.5)
так как рассматривается одна кривая q(V), для
|
q |
С , |
(7.6) |
|
V |
||||
|
|
|
183
