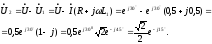Основы электротехники и электроники Лабораторная работа n 4 Исследование установившегося синусоидального режима методом комплексных амплитуд
Цель работы: привить практические навыки анализа электрических цепей методом комплексных амплитуд.
1. Теоретическая часть
Метод комплексных амплитуд основан на представлении синусоидальных функций через экспоненты с мнимым аргументом. Все расчеты по этому методу проводят с помощью алгебры комплексных чисел.
Аналитически комплексное число можно представить в алгебраической, тригонометрической и показательной формах:
z = a + jb = A (cos + jsin) = Aej.Здесь a и b - вещественная и мнимая составляющие; А - модуль и - аргумент комплексного числа.
Комплексное сопряженное число имеет вид
z* = a - jb = A (cos - jsin) = Ae-j.
Если взять сумму и разность комплексного числа и его сопряженного, то для косинуса и синуса имеем следующие представления:
Acos = Re[Aej] = 1/(2) ( Aej + Ae-j);
Asin = Im[Aej] = 1/(2j) ( Aej - Ae-j).
Для синусоидальной функции времени u(t) = Umcos(t + u) амплитуда A = Um и аргумент = t + u линейно возрастают во времени. Поэтому комплексная величина
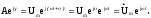
Первый множитель в этом выражении
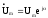
называется комплексной амплитудой. Модулем комплексной амплитуды является вещественная амплитуда синусоидальной функции, а аргументом - начальная фаза, так что одна величина (комплексная амплитуда) включает в себя оба параметра синусоиды: амплитуду и начальную фазу.
На
плоскости комплексных амплитуд
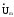 будет изображаться вектором, аргумент
которого равен начальной фазе , а длина
пропорциональна вещественной амплитуде
будет изображаться вектором, аргумент
которого равен начальной фазе , а длина
пропорциональна вещественной амплитуде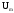 .
.
Комплексное сопротивление
Комплексное сопротивление представляет отношение комплексных амплитуд напряжения и тока и является комплексной величиной, зависящей от параметров цепи и частоты приложенного сигнала:
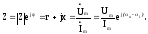
Модуль и аргумент сопротивления равны соответственно отношению вещественных амплитуд и разности начальных фаз напряжения и тока:
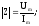 = u
- i.
= u
- i.
Вещественную и мнимую части Z называют активной и реактивной составляющими комплексного сопротивления.
Величина, обратная комплексному сопротивлению, представляющая отношение комплексных амплитуд тока и напряжения, называется комплексной проводимостью:
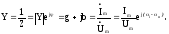
Ее модуль и аргумент являются величинами, обратными комплексному сопротивлению:

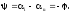
Введение комплексных сопротивлений и проводимостей, коэффициентов пропорциональности между комплексными амплитудами напряжения и тока означает введение закона Ома в комплексной форме для установившихся синусоидальных режимов:

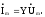
В отличие от закона Ома для постоянного тока выражения связывают комплексные величины; это отражает тот факт, что в случае синусоидальных напряжений и токов кроме амплитуд необходимо знать сдвиг фаз между ними. Если известно комплексное сопротивление, то по заданной комплексной амплитуде напряжения можно найти комплексную амплитуду тока.
Отсюда следует вывод о том, что комплексное сопротивление определяет вынужденную реакцию двухполюсных цепей, т.е. цепей с двумя внешними выводами, к которым приложен сигнал синусоидальной формы.
Первый закон Кирхгофа:
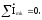
В установившемся синусоидальном режиме сумма комплексных амплитуд токов в узле электрической цепи равен нулю.
Второй закона Кирхгофа:
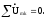
В установившемся синусоидальном режиме сумма комплексных амплитуд напряжений в контуре равна нулю.
При использовании законов Кирхгофа и Ома в комплексной форме расчет цепей в установившемся режиме получается аналогичным расчету цепей постоянного тока, лишь сопротивления и все переменные будут комплексными величинами в силу необходимости учета фазовых соотношений, кроме соотношений между амплитудами.
Характеристики элементов цепи в синусоидальном режиме
Резистивный элемент
Подставив в выражение в.а.х. элемента для мгновенных значений
i = Gu, получим Imcos(t + i) = Gumcos(t + u).
Приравнивание амплитуд и начальных фаз дает
Im = Gum; i = u.
В резистивном элементе ток и напряжение совпадают по фазе и отношение их амплитуд равно проводимости.
Подставим теперь в выражение в.а.х. комплексные амплитуды:

Комплексные проводимость и сопротивление имеют только вещественные составляющие:
Y = G; и Z = R.
Аргумент = - указывает на совпадение фаз напряжения и тока.
Индуктивный элемент
Подстановка в основное соотношение для индуктивного элемента u = Ldi/dt дает

Отсюда u = i +/2; Um = Lim = xLIm.
Напряжение
на индуктивности опережает по фазе ток
на 90,
а
отношение амплитуд напряжения и тока
определяется величиной, называемой
индуктивным
сопротивлением:
 .
.
Подстановка в основное соотношение для индуктивного элемента комплексных величин напряжения и тока дает
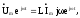
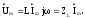

Отсюда получаем, что комплексные сопротивление и проводимость индуктивного элемента имеют только реактивные (мнимые) составляющие
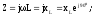
Угол сопротивления = 90 указывают на то, что напряжение опережает по фазе ток; модуль сопротивления равен индуктивному сопротивлению.
Емкостной элемент
Подставив выражения для синусоидальных токов и напряжений в соотношение для емкости получим
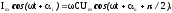
Отсюда


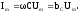
Ток в емкости опережает по фазе напряжение на 90, а отношение амплитуд напряжения и тока называется емкостным сопротивлением
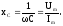
Подстановка комплексных значений тока и напряжения в соотношение для емкости получим комплексное сопротивление емкости, которое имеет только комплексную составляющую:
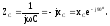
Емкость является также реактивным элементом.
Применение метода комплексных амплитуд к анализу установившегося
синусоидального режима в линейных цепях
После введения понятия комплексного сопротивления, комплексных сопротивлений и проводимостей основных элементов цепи, а также установления законов Кирхгофа для комплексных амплитуд токов и напряжений нет необходимости в предварительном составлении системы дифференциальных уравнений цепи во временной области и последующем их преобразовании в алгебраические уравнения для комплексных амплитуд.
При
анализе по методу комплексных амплитуд
удобно каждый элемент цепи представлять
своим комплексным сопротивлением или
комплексной проводимостью, а токи и
напряжения, как искомые, так и источников,
- комплексными амплитудами. В результате
получается комплексная схема
замещения.
На этой схеме каждую двухполюсную ветвь
можно изобразить виде резистора с
записанным значением комплексного
сопротивления. в результате схема будет
иметь вид резистивной цепи, только
вместо вещественных будут комплексные
величины: R
Z(j); G Y();
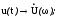
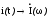 .
.
Уравнения равновесия для комплексных амплитуд составляются по комплексным схемам замещения аналогично резистивным цепям. Поэтому для анализа установившегося режима можно принять все методы, которые были разработаны для резистивных цепей.
Особенность цепей в синусоидальном режиме состоит в том, что сопротивления реактивных элементов зависят от частоты входного сигнала. Поэтому от частоты будут зависеть основные параметры цепи и, следовательно, все переменные. Для выявления свойств цепи в синусоидальном режиме необходимо исследовать основные параметры цепи при изменении частоты в диапазоне от 0 до . Соответствующие зависимости параметров цепи от частоты называются частотными характеристиками. В некоторых случаях интересуются поведением цепи в ограниченном диапазоне частот или при одной заданной частоте. Анализ по методу комплексных амплитуд называют также анализом в частотной области.
Пример
На
рис.1 показана цепь, в которой R1=0.5,
L1=0,5,
R2=0,5,
L2=0,5,
C=2.
Напряжение на входе равно

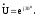
Сопротивления ветвей цепи: Z2 = R1 + jL =0,5 + j0,5; ZC = 1/ jC = -j0,5; Z2 = R2 + jL2 = 0,5 + j0,5.

R1
L1
2

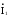
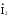
 R2
R2
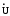 C L2
Рис.1.
C L2
Рис.1.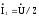 вх.Zвx
вх.Zвx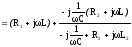 =
=
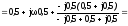
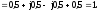
Ток