
Основы электротехники и электроники Лабораторная работа n 2 Расчет электрических цепей методом контурных токов и узловых потенциалов
Цель работы:привить практические навыки расчета электрических цепей методом контурных токов и узловых потенциалов.
1. Теоретическая часть
1.1. Метод контурных токов
При расчете методои контурных токов полагают, что в каждом независимом контуре схемы течет свой контурный ток. Уравнения составляют относительно контурных токов, после чего определяют токи веивей через контурные токи. число неизвестных в этом методе равно числу уравнений, которые необходимо было бы составить для схемы по второму закону Кирхгофа. Следоательно, метод контурных токов более экономен при вычислительной работе, чем метод на основе законов Кирхгофа (в нем меньшее число уравнений).



























 R2
R3
i1
i3
i2
R1
I11
R5
I22
R4
U1
+ U2
- U3
+
- +
-
Рис.
1.1.
R2
R3
i1
i3
i2
R1
I11
R5
I22
R4
U1
+ U2
- U3
+
- +
-
Рис.
1.1.
- U1 + (R1 + R2)I11 + R5(I11-I22) - U2 = 0 или
(R1 + R2 + R3)I11 + (- R5)I22 = U1 + U2.
Для второго контура
U2- R5(I11- I22) + (R3+ R4)I22+ U3= 0 или
(- R5)I11 + (R3 + R4 + R5)I22 = - U2 - U3.
Перепишем эти уравнения следующим образом
R11I11 + R12I22 = U11 (1.1)
R21I11 + R22I22 = U22
Здесь R11= R1 + R2 + R5, R22= R3 + R4 + R5, R12=R21=-R5,
U11= U1 + U2, U22 = - U2 - U3.
Решая систему линейных алгебраических уравнений (1.1) находим токи I11и I22. Если в результате решения системы уравнений какой-либо контурный ток окажется отрицательным, то это будет означать, что в действительности направление контурного тока обратно принятому за положительное.
В ветвях, не являющихся смежными между соседними контурами( в ветви с сопротивлениями R1, R2и R3, R4), найденный контурный ток будет являться истинным током. В смежных ветвях истинные токи находят через контурные В ветви с сопротивлением R5протекающему сверху вниз ток равен разности I11- I22.
Пример 1.1.
Пусть в схеме на рис.1.1 U1= 5 В, U2= 10 В, U3= 4 В, R1 = 2 Ком, R2 = 3 Ком, R3 = 4 КОм,
R4 = 6 Ком, R5 = 10 Ком. Найти токи в схеме.
Решение. R11= R1+ R2+ R3= 2 + 3 + 10 = 15 Ком.
R22= R3+ R4+ R5= 4 + 6 + 10 = 20 Ком.
R12= R21= - 10 Ком.
U11= U1+ U2= 5 + 10 = 15 В.
U22= - U2- U3= - 10 - 4 = 14 В.


















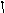

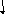
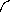
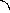


 R1
i1
i3
i2
Iк
I11
R2
I22
R3
U1
-
+
Рис.
1.2.
R1
i1
i3
i2
Iк
I11
R2
I22
R3
U1
-
+
Рис.
1.2.
15 I11 - 10 I22 = 15
-10 I11 +20 I22 = -14 .
Умножая первое уравнение на 2 и складывая их получим
20 I11 = 16, I11 = 0.8 мА.
I22 = - 0.3 мА.
I1 = I11 = 0.8мА,
I2 = I11 - I 22 = 0.8 - (-0.3) = 1.1мА,
I3 = -I22 =0.3мА.
Составлению уравнений по методу контурных токов для схем с источниками токаприсущи некоторые особенности. В этом случае полагаем, что каждая ветвь с источником тока входит в контур, замыкающийся через ветви с источниками напряжения и сопротивлениями, и что эти токи известны и равны токам соответствующих источников тока. Уравнения составляют лишь для контуров с неизвестными контурными токами.
Для схемы на рис. 1.2 ток источника Iк= I11, т.к. течет согласно направления контурного тока I11. Для определения неизвестного тока I22достаточно составить одно уравнение
R2(I22 - Iк) + I22R3 - U1 = 0.
I22 = (U1 + R2Iк) / (R3 + R2).
I2 = Iк - I22.
Пример 1.2.Пусть U1= 16В, R2= 2ком, Iк =2мА, R3= 5 Ком. Тогда
I22= (16 + 22) / (5 + 2) = 2.86 мА. I2= 2 - 2.86 = -0.86мА.
