3. Пример расчета схемы

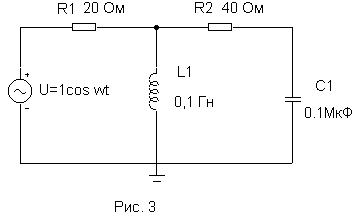
Пусть требуется определить установившееся синусоидальное напряжение на емкости схемы, показанной на рис.3. Величины элементов схемы приведены на схеме. Расчет провести для частоты, равной

.

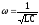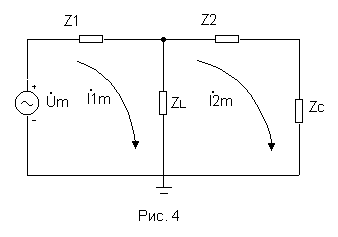
Для решения задачи воспользуемся методом комплексных амплитуд и перейдем к схеме замещения рис.4. Здесь Z₁=R₁, Z₂=R₂, Z_L=jL, Z_C=1/jC.

Расчет цепи будем вести в общем виде, т. к полученное выражение будет использоваться в следующей лабораторной работе для определения частотных характеристик электрической цепи. Для определения напряжения на емкости можно воспользоваться известными методами расчета электрических цепей постоянного тока, например, методом контурных токов. Для упрощения записи введем обозначение j = p и запишем уравнения для контурных токов I_1m и I_2m. Также для упрощения записи в дальнейшем опустим индекс m для токов и напряжений

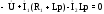(1)

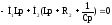(2)

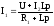
Из уравнения (1) найдем ток и подставим его в уравнение (2). После несложных алгебраических преобразований найдем ток

.

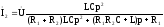Обратите внимание на форму записи выражения для тока. Ток представлен в виде отношения двух полиномов переменной p = j. Из такой формы записи легко перейти к дифференциальному уравнению, описывающему работу схемы во временной области, найти функцию передачи электрической цепи, по которой можно найти частотные характеристики цепи.

Напряжение на емкости найдем путем умножения тока 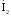на комплексное сопротивление емкости.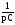

.

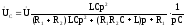Сократив на pC, получим

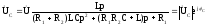. (3)

После получения формулы целесообразно убедиться в правильности ее вывода. Для этого можно решить задачу другим способом и сравнить полученные результаты. Однако, существует простой способ, позволяющий определить грубые ошибки, допущенные при выводе формулы. Для этого можно проверить размерности правой и левой частей формулы. Они должны совпадать. Размерности сопротивления индуктивности, емкости и переменной p можно выразить через размерности тока, напряжения и времени .

Подставим в формулу (3) размерности величин и убедимся, что размерности правой и левой части уравнения совпадают

.

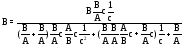Найдем модуль и фазу .

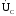Модуль будет равен

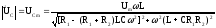. (4)

Подставив в выражение (4) величины элементов электрической цепи и амплитуду входного напряжения U, найдем амплитуду напряжения на емкости для частоты 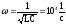. Она равна 0,9992 В.

Фаза напряжения на емкости .

.

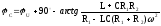Обратите внимание на вычисления функции арктангеса. Знаменатель арктангеса отрицательный, следовательно, угол лежит во второй четверти и равен

.

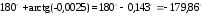Итак, фаза напряжения на емкости равна

.

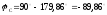Теперь можно записать напряжение на емкости как функцию времени

,

где .

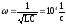4. Контрольные вопросы

1. Что такое комплексная амплитуда?

2. Как записать гармонический сигнал в комплексной форме?

3. Дайте определение комплексному сопротивлению.

4. Сформулируйте закон Ома в комплексной форме.

5. Сформулируйте законы Кирхгофа в комплексной форме.

6. Чему равно комплексное сопротивление резистивного, индуктивного и емкостного элементов?

7. В каких случаях применяется метод комплексных амплитуд?

8. В чем состоит метод расчета электрических цепей методом комплексных амплитуд?

9. Как определить модуль и фазу комплексного выражения?