4.6 Модель эллипсоида

Эллипсоид в графической базе данных задается следующими параметрами:

• r – радиус эллипсоида;

• h – половина высоты эллипсоида;

• n – количество разбиений на вертикальной полуокружности,

• m – количество разбиений на горизонтальной полуокружности.

Рассмотрим построение геометрической модели эллипсоида с помощью меридиан и параллелей, центр локальной системы координат свяжем с геометрическим центром эллипсоида, оси которой направлены произвольно. Построение геометрической модели представлено на рисунке 4.6.

z

y

x

0

β

α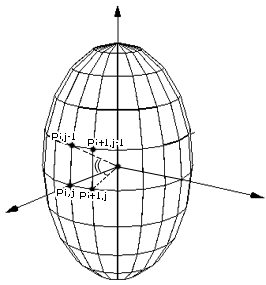

Рисунок 4.6 – Модель эллипсоида

Построение эллипсоида начинаем с построения точки с координатами Р₀₀(0, 0, r). Затем строится нулевой меридиан (кривая разбивается на n точек) по формуле:

(4.9)

,

где - коэффициент растяжения;

- угол поворота.

Построенная ломаная, точки P0,0…Pn,0 - нулевой меридиан.

Построение параллелей производится путем вращения нулевого меридиана вокруг оси Z на угол α = 2π/m.

Следовательно, в графической базе данных модель эллипсоида можно задать с помощью формулы (4.10):

Эллипсоид(r,h,n,m) (4.10)

где r – радиус эллипсоида, h – высота половыны эллипсоида, n - количество меридиан, m - количество параллелей.

4.7 Геометрическая модель косоугольного конуса

Косоугольный конус задаётся четырьмя параметрами: высота, радиус основания, смещение вершины конуса относительно центра основания вдоль оси OX, количество разбиений основания. Обозначим эти параметры соответственно буквами h, r, s и n.

Пусть центр основания совпадает с началом локальной системы координат, а часть конуса без основания находится со стороны положительного направления оси OZ. Первая точка основания имеет координаты A₁=(0, r, 0). Тогда координаты остальных точек снования будем находить по следующей формуле:

A_i+1= A_i*ПоворотOZ(360/n), (4.11)

а координаты вершины конуса будут равны (s, 0, h).

Вид геометрической модели косоугольного конуса приведен на рисунке 4.6.

Рисунок 4.6 – Вид геометрической модели косоугольного конуса

4.8 Геометрическая модель пирамиды с пятиугольным основанием

Пирамида с пятиугольным основанием задаётся двумя параметрами: высота и радиус окружности, в которую вписано основание. Обозначим эти параметры соответственно буквами h и r.

Пусть центр основания совпадает с началом локальной системы координат, а часть пирамиды без основания находится со стороны положительного направления оси OZ. Первая точка основания имеет координаты A₁=(0, r, 0). Тогда координаты остальных точек снования будем находить по следующей формуле:

A_i+1= A_i*ПоворотOZ(360/5), (4.12)

а координаты вершины конуса будут равны (0, 0, h).

Вид геометрической модели пирамиды с пятиугольным основанием приведен на рисунке 4.7.

Рисунок 4.7 – Вид геометрической модели пирамиды с пятиугольным основанием

4.9 Геометрическая модель усечённой пирамиды с трёугольным основанием

Данный объект задаётся тремя параметрами: высота, радиус окружности, в которую вписано нижнее основание и радиус окружности, в которую вписано верхнее основание. Обозначим эти параметры соответственно буквами h, r1 и r2.

Пусть центр нижнего основания совпадает с началом локальной системы координат, а часть пирамиды без этого основания находится со стороны положительного направления оси OZ. Первая точка нижнего основания имеет координаты A₁₁=(0, r1, 0), а первая точка верхнего основания A₂₁=(0, r2, h). Тогда координаты остальных точек нижнего снования будем находить по следующей формуле:

A_1i+1= A_1i*ПоворотOZ(360/3), (4.13)

а координаты точек верхнего основания – по формуле:

A_2i+1= A_2i*ПоворотOZ(360/3). (4.14)

Вид геометрической модели усеченной пирамиды с треугольным основанием приведен на рисунке 4.8.

Рисунок 4.8 – Геометрическая модель усечённой пирамиды с трёугольным основанием

4.10 Моделирование икосаэдра

Для построения икосаэдра (рис. 4.9) используется цилиндр радиуса R , ось Z которого совпадает с осью цилиндра, а основание находится друг от друга на расстоянии ± h/2.

Рисунок 4.9 Построение икосаэдра

Каждое из окружностей оснований разбивается на 5 равных сегментов, и точки окружности последовательно соединяются между собой. Вращаясь против часовой стрелки на угол φ = 2*π /5, выбираются точки на первой и на второй окружности соответственно.

На высоте: выбираются вершины P'₀ и P''₀ и соединяются с вершинами в основании (верхнего и нижнего соответственно).

Остальные вершины получаются с помощью матрицы поворота:

P’_i= P’_i-1*Поворот(2*π/5) (4.1)

P"_i= P”_i-1*Поворот(2* π /5) (4.2)

Модель построенного икосаэдра изображена на рисунке 4.10.

Рисунок 4.10 – Модель икосаэдра

4.11 Геометрическая модель додекаэдра

Построение додекаэдра осуществляется при помощи икосаэдра.

Ниже приведены краткие шаги данной операции.

1. Построение икосаэдра;

2. Определение геометрических центров каждой из граней;

3. Соединение геометрических центров.

Для построения икосаэдра используется цилиндр единичного радиуса R, ось которого совпадает с осью OZ, и основание находится соответственно на высоте . Каждая из окружностей разбивается на 5 равных сегментов, и точки на окружности последовательно соединяются между собой.

Двигаясь против часовой стрелки с шагом α=2π/n, выбираются точки то на одной, то на другой окружности. Далее происходит попарно соединение точек. На высоте берется окончательная вершина.

В графической базе данных додекаэдр можно представить в виде:

Додекаэдр(W), (4.15)

где w – длина стороны.

На рисунке 4.11 изображена геометрическая модель додекаэдра.

Рисунок 4.11 – Геометрическая модель додекаэдра

5 ПОШАГОВОЕ ПОСТРОЕНИЕ МОДЕЛИ СЛОЖНОГО ОБЪЕКТА

5.1 Декомпозиция сложного объекта

Моделью сложного трехмерного объекта, согласно заданию, является модель робота-краба, которая состоит из таких базовых примитивов как: эллипсоид, икосаэдр, призма с треугольным основанием, сфера, косоугольный цилиндр, усеченная пирамида с треугольным основанием, полусфера, косоугольная призма с треугольным основанием.

Модель робота-краба состоит из лап (призма с треугольным основанием, икосаэдр, усеченная пирамида с треугольным основанием), лап (косоугольный цилиндр) с клещнями (косоугольная призма с теугольным основанием), глаз (сфера), тело (полусфера, элипсоид).

5.2 Параметрические модели примитивов

Лапа состоит из следующих примитивов:

- призма с треугольным основанием Prizm3(r1, h1);

- икосаэдр Iko(r2);

- усеченная пирамида с треугольным основанием Piramid3(r3, r4, h2,).

Лапа с клещами состоит из следующих примитивов:

- косоугольный цилиндр Cyl(r5, h3, n1,m1)*M(сдвига);

- косоугольная призма с теугольным основанием KosPr(r6, h4)* *M(сдвига).

Глаз состоит из следующих примитивов:

- сфера Sphere (r7, n2, m2).

Тело состоит из следующих примитивов:

- полусфера Halfsphere(r8, n3, m3)*M(отсечения);

- элипсоид Elips(r9, n4, m4)*M(сжатия),

где r(i) – радиус, h(i) – высота, n(i), m(i) - число разбиения, М – матрица.

n1=n2=n3=n

m1=m2=m3=m

Запишем значения параметром фигур через r7:

h1=20*r7;

h2=r7;

h3=18*r7

h4=4*r7

r1=1.5*r7;

r2=r7;

r3=r7;

r4=2*r7;

r5=1.5*r7;

r6=1.5*r7;

r8=9*r7

r9=12*r7;

5.3 Пошаговое построение сложного объекта

Строим тело:

- Стоим элипосид:

Строим сферу радиусом 12*r7, умножаем на матрицу сжатия М(0.8, 1, 0.25), получаем элипсоид (рисунок 5.1).

Z

Y

X

Рисунок 5.1 – Эллипсоид

Строим полусферу:

- cтроим сферу радиусом 9*r7. Отсекаем пол сферу по оси –OZ.

Полученная фигура будет телом (рисунок 5.2).

Z

-X

Y

Рисунок 5.2- Тело

Строим глаза:

1 глаз:

- cтроим сферу радиусом r7. Переносим на (4*r7, 3*r7, 8*r7);

2 глаз:

- строим сферу радиусом r7. Переносим на (-4*r7, 3*r7, 8*r7).

Полученная фигура будет телом с глазами (рисунок 5.3)

Z

-X

Y

Рисунок 5.2- Тело с глазами

Строим лапы:

- строим призму с треугольным основанием:

- строим цилиндр с числом разбиения равным 3, радиуса 1.5*r7 и высотой 20*r7;

- строим икосаэдр

строим икосаэдр радиусом r7 и перемещаем на (0, 0, 20*r7);

- строим усеченную призму с треугольным основанием:

строим цилиндр с числом разбиения равным 3, радиусами r7, 2*r7 и высотой r7, поворачиваем вокруг оси OY на -90 градусов, перемещаем на (0, 0, 3*h-2/5h).

1 лапа:

- поворачиваем построенные фигуры на 90 градусов вокруг оси OX и 45 градусов вокруг оси OZ;

2 лапа:

- поворачиваем построенные фигуры на 90 градусов вокруг оси OX и -45 градусов вокруг оси OZ;

3 лапа:

- поворачиваем построенные фигуры на -90 градусов вокруг оси OX и 45 градусов вокруг оси OZ;

4 лапа:

- поворачиваем построенные фигуры на -90 градусов вокруг оси OX и -45 градусов вокруг оси OZ;

Полученная фигура будет содержать лапы (рисунок 5.3)

Z

-X

Y

Рисунок 5.3 - Фигура с лапами

Строим лапы с клещнями:

- строим косоугольный цилиндр:

- строим цилиндр радиусом 1.5*r7, высотой 20*r7, сдвигаем по оси OY на 0.1*r7

- строим косоугольную призму с треугольным основанием:

- строим цилиндр с числом разбиения равным 3, радиусом 1.5*r7, высотой 18*r7, сдвигаем по оси OX на 0.1*r7, перемещаем на 4*r7;

- Поворачиваем полученные фигуры на 90 градусов вокруг оси OX.

1 лапа с клещней:

- поворачиваем полученные фигуры на 30 градусов вокруг оси OY;

2 лапа с клещней:

- поворачиваем полученные фигуры на -30 градусов вокруг оси OY.

Получили робота-краба (рисунок 5.4)

Z

-X

Y

Рисунок 5.4 - Робот-краб