3 Анализ графических и геометрических методов

3.1 Системы координат

3.1.1 Декартова система координат

Прямоугольная, или Декартова система координат — наиболее простая и поэтому часто используемая система координат в пространстве.

Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно одинаковы для всех осей (что не является обязательным). OX — ось абсцисс, OY — ось ординат, OZ — ось аппликат.

Если большой палец правой руки принять за направление X, указательный за направление Y, а средний за направление Z, то образуется правая система координат. Аналогичными пальцами левой руки образуется левая система координат. Иначе говоря, положительное направление осей выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY, если этот поворот наблюдать со стороны положительного направления оси OZ. Правую и левую системы координат невозможно совместить так, чтобы совпали соответствующие оси (см. рис. 3.1).

Рисунок 3.1. Декартова система координат

Положение точки A в пространстве определяется тремя координатами x, y и z. Координата x равна длине отрезка OB, координата y — длине отрезка OC, координата z — длине отрезка OD в выбранных единицах измерения. Отрезки OB, OC и OD определяются плоскостями, проведёнными из точки A параллельно плоскостям YOZ, XOZ и XOY соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A, координата z — аппликатой точки A. Записывают так: A(x,y,z).

3.1.2 Векторная система координат

Для векторной системы координат, как и для декартовой, характерно задание прямых, направлений и единичных отрезков, но в отличие от декартовой, в ней устанавливает взаимно однозначное соответствие между векторами пространства и упорядоченными тройками действительных чисел, а не между числами и точкой. Любой вектор р заданный тройкой чисел представляет собой направленный отрезок исходящий из точки O в точку Р.

Векторная система координат показана на рисунке 3.2.

Рисунок 3.2 - Векторная система координат

3.1.3. Аффинная система координат

Аффинная система координат является объединением декартовой и векторной систем координат и устанавливает взаимно однозначное соответствие между точками, векторами пространства и упорядоченными тройками действительных чисел.

3.1.4 Однородные координаты точки

Для n-мерного пространства в одно­родных координатах вершины всегда задаются n+1 координатами. Основное удобство применения одно­родных координат заключается в том, что с их помощью все виды преобразований координат могут быть представлены в единой форме. Они были введены в геометрии и впоследст­вии использованы в графике. В однородных координатах положение точки Р(х, у, z) записывается как P(W*x, W*y, W*z, W) или P(X, Y, Z, W), для лю­бого масштабного множителя, причем трехмерные декартовы координаты легко определяются:

х = X/W; у = Y/W; z = Z/W (3.1)

То есть привычная для нас ортогональная система координат получается как проекция однородной системы на плоскость W = 1.

Таким образом для преобразования точки из обычных координат в однородные нужно добавить компоненту равную 1 и умножить все компоненты на любое вещественное число. Для преобразования точки из однородных координат в обычные координаты разделите все компоненты на последний компонент и отбросьте его.

3.2 Аффинные преобразования в пространстве

Аффинные преобразования - это комбинация линейных преобразований, переводящие параллельные прямые в параллель­ные, скрещивающиеся в скрещивающиеся и сохраняющие величину отношения длин отрезков параллельных прямых. Они допускают компактное матричное представление. Аффинные преобразования в однородных координатах описываются матрицами 4*4. Пусть есть некоторая точка P и некоторое аффинное преобразование, которому соответствует матрица М. Тогда результирующая точка P’ для данного аффинного преобразования и данной точки может быть вычислена по формуле:

Используя матрицы аффинных преобразований, получают координаты точки после преобразования по координатам исходной точки. Используя матрицу, обратную матрице преобразования, по координатам результирующей точки получают координаты исходной точки. Композиция нескольких аффинных преобразований в одно представляется в матричном виде как произведение матриц составляющих сложного преобразования в порядке их применения к точке. Основными аффинными преобразованиями принято считать преобразования переноса, поворота и масштабирования. Также от­дельно выделяют преобразование отражения и сдвига.

3.2.1 Преобразования переноса

Перенос точки Р на вектор (x,y,z) осуществляется при помощи умножения вектора координат точки Р на матрицу переноса. Матрица переноса имеет вид:

(3.1)

Перенос точки Р в точку Р’ показан на рисунке 3.3.

Рисунок 3.3 – Перенос точки Р в точку Р’

3.2.2 Преобразования поворота

Одной из основных операций аффинных преобразований является поворот фигуры относительно заданной точки на некоторый угол. Осуществляется он при помощи умножения координат фигуры на матрицу поворота. Матрицы поворота вокруг заданных осей на угол r имеют вид:

Вокруг оси абсцисс: 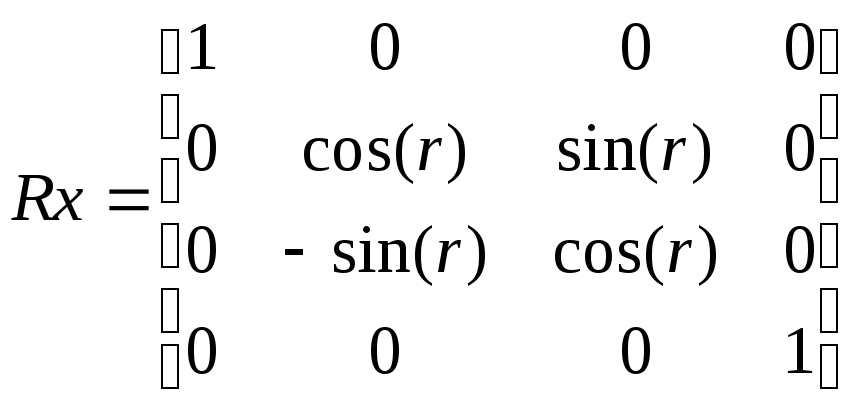(3.2)

Вокруг оси ординат: 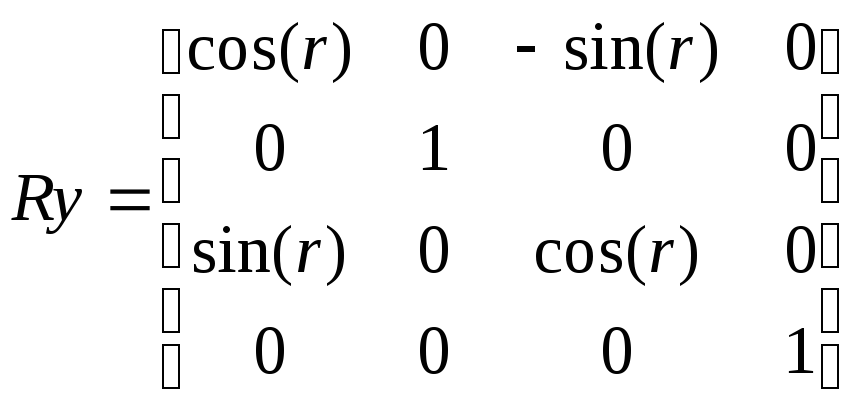(3.3)

Вокруг оси аппликат: (3.4)

На рисунке 3.4 приведены три основных положительных поворота.

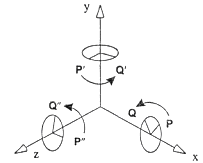
Рисунок 3.4 – Положительные повороты вокруг осей

3.2.3 Преобразования масштаба

Масштабирование изменяет размер фигуры и использует три масштабных множителя — S_x , S_y и S_z для координат x, у и z соответственно.

Более строго такой способ масштабирования называется масштабированием относительно начала отсчета, поскольку каждая точка передвигается в S_x раз дальше от начала отсчета в направлении х, в S_y раз дальше от начала отсчета в направлении y и в S_z раз дальше от начала отсчета в направлении z. Матрица масштабирования имеет вид:

( 3.5)

3.2.4 Преобразования отражения

Если масштабный множитель отрицателен и равен 1, то происходит отражение относительно координатных плоскостей. Матрицы отражения относительно плоскостей YОZ, XОZ и XОY имеют вид:

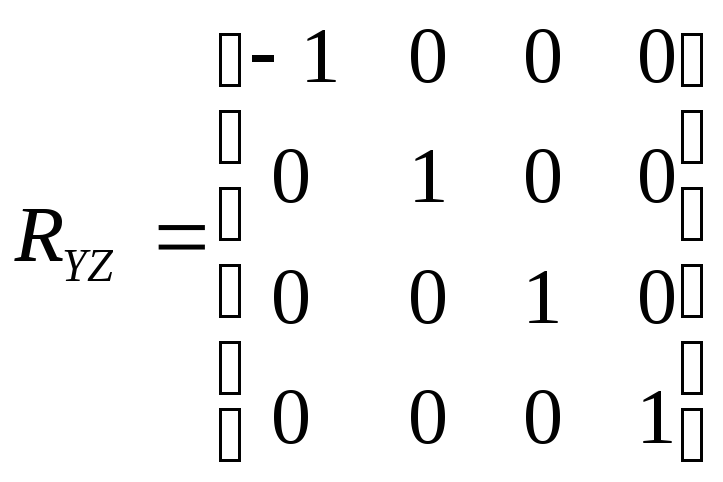(3.6);

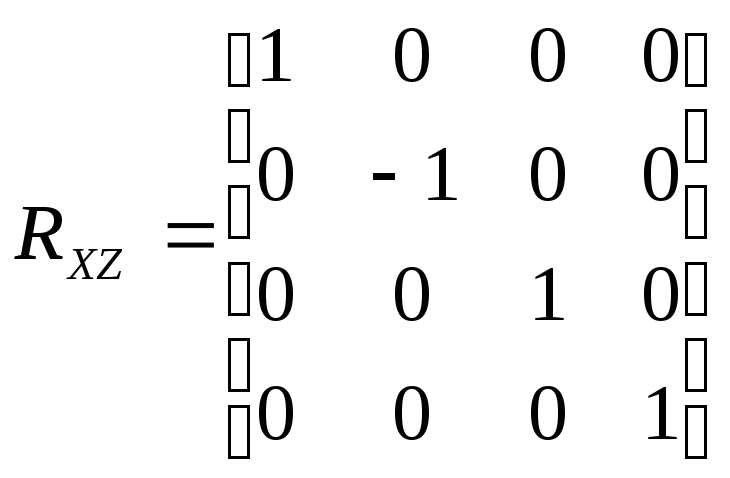(3.7);

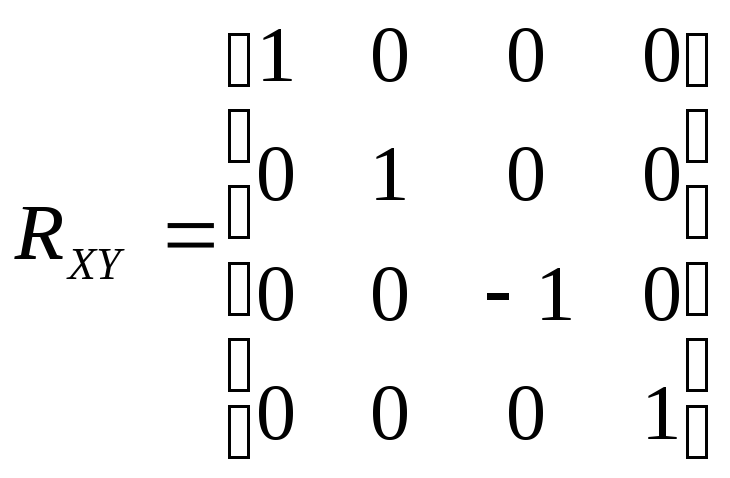(3.8);

На рисунке 3.5 приведен пример отражения точки А относительно плоскости XОY.

Рисунок 3.5 – Преобразование отражения относительно плоскости XOY

3.2.5 Преобразования сдвига

На рис. 3.6 приведен пример сдвига вдоль оси ОХ.

Рисунок 3.6 – Двумерный сдвиг относительно оси OХ

В этом случае координата у каждой точки остается неизменной, а каждая координата х перемещается на величину, которая линей­но возрастает с ростом у. Трехмерный сдвиг описывается следующей матрицей:

(3.9)

Здесь Shx, Shy, Shz – параметры сдвига вдоль осей OX, OY, OZ соответственно.

3.3 Проецирование. Виды проецирования

Несоответствие между пространственными объектами и плоскими изобра­жениями устраняется путем введения проекций, которые отображают объек­ты на картинной двумерной проекционной плоскости.

Проецированием называется процесс получения изображения объекта на проецирующей (картинной) плоскости путем помещения всех точек объекта на эту плоскость. Для получения нормального изображения необходимо, чтобы над каждой точкой объекта выполнялось одинаковое преобразование. В общем случае различают два типа проецирования: параллельное и центральное (см. рис. 3.7). Каждый из этих двух типов имеет свои подтипы.

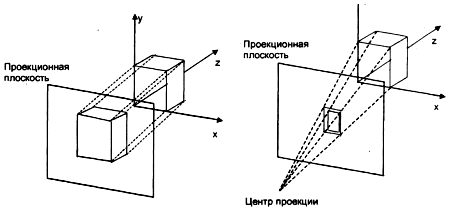
Рисунок 3.7 – Параллельное (слева) и центральное проецирование

3.3.1 Параллельное ортографическое проецирование

Параллельное проецирование на картинную плоскость проводится пучком параллельных прямых, проходящих под определённым углом к картинной плоскости. В случае ортографического проецирования в качестве картинной плоскости выступает одна из координатных плоскостей, а пучок параллельных прямых перпендикулярен ей. Математически параллельное ортографическое проецирование выражается в обнулении координаты точки, соответствующей оси, перпендикулярной проецирующей плоскости. Матрица ортографического проецирования получается из единичной матрицы путем обнуления соответствующего диагонального элемента. Так, матрицы проецирования на плоскости ХOY , YOZ , ХOZ будут следующими:

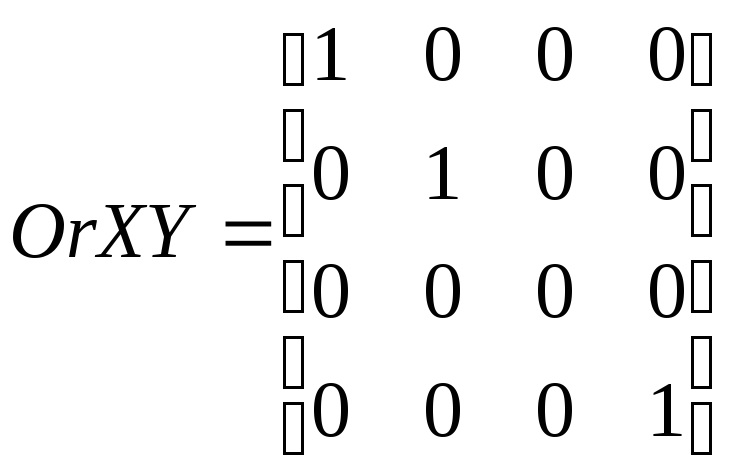(3.10)

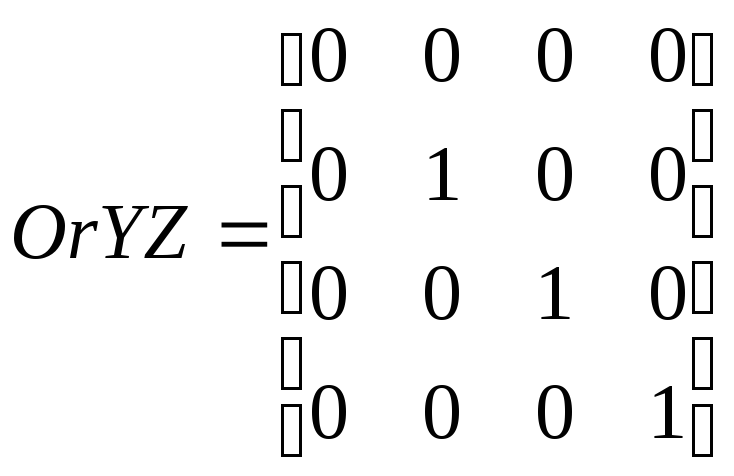(3.11)

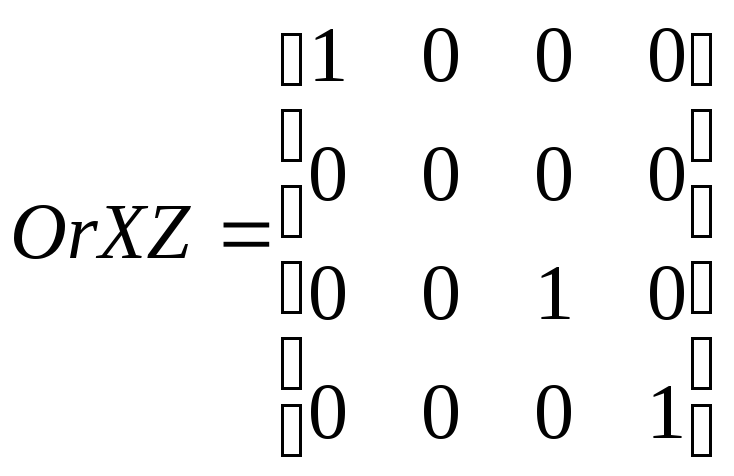(3.12)

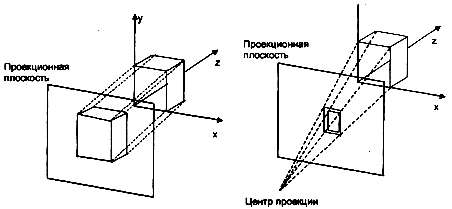
Рисунок 3.8 – Параллельное проецирование

3.3.2 Параллельное косоугольное проецирование

Косоугольная проекция формируется параллельными проекторами с центром, лежащим в бесконечности, и расположенными под косым углом к плоскости проекции. Общая схема проекции изображена на рисунке 3.9.

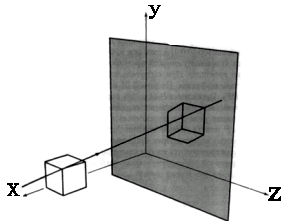
Рисунок 3.9 – Параллельное косоугольное проецирование

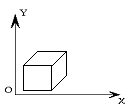
Особый интерес представляет косоугольные проекции кавалье (свободная). Проекция кавалье получается, когда угол между проекторами и плоскостью проекции составляет 45°. В этой проекции коэффициенты искажения для всех трех главных направлений одинаковы. Результат этой проекции выглядит неесте­ственно утолщенным. Матрица проекции кабине на плоскость XOY имеет следующий вид:

(3.13)

Здесь ƒ — длина спроецированного единичного вектора на оси z, т.е. коэффициент искажения, а α — угол между горизонталью и спроецированной осью z.

На рисунке 3.10 изображена свободная проекция куба.

Рисунок 3.10 – свободная проекция куба

3.3.2 Изометрическое проецирование

Изометрия является разновидностью аксонометрического проецирования. Изометрией называется такое параллельное проецирование, при котором вектор нормали картинной плоскости (плоскости проецирования) попарно образуют одинаковые углы с ортами координатных осей (рисунок 3.11).

Рисунок 3.11 – Пример изометрического проецирования

Плоскость проецирования пересекает координатные оси в точках dx, dy, dzи задается нормальным векторомN(перпендикулярен плоскости проецирования). Путем параллельного проецирования точкаАпроецируется в точкуА'на плоскость (dx, dy, dz).

По определению изометрического проецирования, вектор Nдолжен образовывать попарно равные углы с ортами координатных осей. Это возможно лишь в случае, когда угол наклона равен 45. Координаты ортонормированного вектораN(N_x, N_y, N_z)вычисляются следующим образом:

. (3.2)

3.3.3 Диметрическая проекция

Диметрическая проекция - это аксонометрическая проекция, у которой коэффициенты искажения по двум осям имеют равные значения, а искажение по третьей оси может принимать иное значение.

В целях упрощения построений, как и в изометрических проекциях, приведенный коэффициент искажения по осям x и z принимают равным 1; по оси y коэффициент искажения равен 0,5. По осям x и z или параллельно им все размеры откладывают в натуральную величину, по оси y размеры уменьшают вдвое. Расположение осей Ox и Oy в диметрической проекции показано на рис. 3.12.

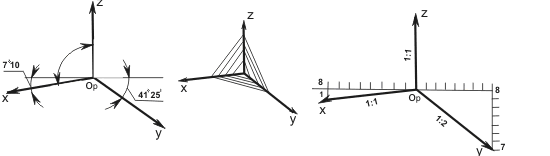
Рисунок 3.12 - Расположение осей Ox и Oy в диметрической проекции показано

Коэффициент искажения по оси y равен 0.47, а по осям x и z - 0.94.

Диметрическую проекцию, как правило, без искажения по осям x и z и с коэффициентом искажения 0.5 по оси y.

Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы.

Если димметрическую проекцию выполняют без искажения по осям x и z то большая ось эллипсов 1, 2, 3 равна 1,06 диаметра окружности, а малая ось эллипса 1 - 0.95, эллипсов 2 и 3 - 0.35 диаметра окружности.

Если диметрическую проекцию выполняют с искажения по осям x и z, то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая ось эллипса 1 - 0.9, эллипсов 2 и 3 - 0,33 диаметра окружности.

3.4 Модели представления объектов

Существует два основных способа представления трехмерных объектов на экране. Первая из моделей - каркасная (проволочная) отображает основные линии, составляющие объект. Проволочная модель реализуется достаточно просто: она задается множеством точек (вершин) объекта и множеством ребер. Каждое ребро представляет собой объединение двух вершин, содержащихся в множестве. Таким образом, при отрисовке на экране виден каркас объекта. Второй вид модели применяется гораздо чаще, она является более практичной, суть ее заключается в задании треугольных граней объекта. Каждая грань определяется как треугольник. Такая модель называется полигональной. Полигональная модель удобна тем, что позволяет применить множество алгоритмов закраски, сортировки, отсечения невидимых граней.

3.5 Управление камерой

3.5.1. Мировая и локальная системы координат

Мировая система координат – общая система координат, заданная началом координат и тремя ортонормированными векторами.

Локальная система координат (система координат связанная с самим объектом) вводит свою точку отсчета и направление координатных осей. В мировой системе координат можно описать бесконечное множество локальных систем координат (например, для каждого объекта).

3.5.2 Модель камеры

Совокупность объектов мировой системы координат определяют сцену. К объектам сцены относятся как трехмерные объекты, так и камеры, задающие видовые операции. Камера управляет проецированием. Каждая камера задается следующими параметрами:

- положение в мировой системе координат; - направление камеры (главная оптическая ось); - угол зрения камеры; - угол поворота относительно главной оптической оси.

Камера показана на рисунке 3.10.

Рисунок 3.10 – Камера

Величина Ө - угол зрения камеры, N — это расстояние от глаза до ближней плоскости, a F — расстояние от глаза до дальней плоскости. N и F должны быть положительными.

3. Типичные преобразования камер

Камера представляет собой обычный объект, заданный в локальной системе координат и определяет перспективные или параллельные проекции. Точка проецирования называется фокусом. В локальной системе координат эта точка находится на главной оптической оси.

Типичные операции управления камерой:

а) зуммирование – изменение угла зрения или расстояния до центральной точки. При зуммировании камера остается на месте. Матрица зуммирования может быть получена путем умножения матриц двух последовательных преобразований: перспективного преобразования и проецирования на плоскость OXZ;

б) панорамирование – камера поворачивается влево вправо. Матрица панорамирования совпадает с матрицей поворота вокруг оси OZ;

в) вертикальное панорамирование – поворот вверх-вниз. Матрица вертикального панорамирования совпадает с матрицей поворота вокруг оси OX;

г) вращение камеры вокруг главной оптической оси. Матрица вращения вокруг главной оптической оси совпадает с матрицей поворота вокруг оси ординат OY’ локальной системы координат. Поворот аналогичен повороту вокруг оси ординат OZ;

д) перенос влево-вправо и вверх-вниз относительно главной оптической оси.

е) наезд и откат камеры – перемещение камеры вдоль главной оптической оси. В этом случае изменяется положение камеры в мировой системе координат;

3.6 Методы удаления невидимых граней

При использовании полигональной модели возникает проблема отрисовки невидимых граней. Проблема заключается в порядке вывода на экран граней объекта. Для решения данной задачи используется несколько подходов.

3.6.1 Алгоритм z-буфера

Одним из самых простых алгоритмов удаления невидимых граней и поверхностей является метод z-буфера (буфера глубины), где для каждого пикселя находится грань, ближайшая к нему вдоль направления проектирования.

Для вывода на картинную плоскость произвольной грани она переводится в растровое представление на картинной плоскости и затем для каждого пикселя этой грани находится его глубина. В случае если эта глубина меньше значения глубины, хранящегося в z-буфере, пиксель рисуется и его глубина заносится в z-буфер.

Грань рисуется последовательно строка за строкой; для нахождения значений используется линейная интерполяция.

Фактически метод z-буфера осуществляет поразрядную сортировку по x и y, а затем сортировку по z, требуя всего одного сравнения для каждого пикселя каждой грани.

Метод z-буфера работает исключительно в пространстве картинной плоскости и не требует никакой предварительной обработки данных. Порядок, в котором грани выводятся на экран, не играет никакой роли.

3.6.2 Алгоритм художника

Пусть имеется некий набор граней (т.е. объект), который требуется нарисовать. Отсортируем грани по удаленности от камеры и отрисуем все грани, начиная с самых удаленных. Довольно распространенная характеристика удаленности для грани ABC - это среднее значение z, mid_z = (A.z+B.z+C.z)/3. Таким образом, суть алгоритма достаточно проста. Однако существует несколько проблем – в некоторых случаях алгоритм вообще не может дать правильного результата, - в каком порядке грани не рисуй, получится неправильно.

3.7 Закраска граней

Основным преимуществом полигональных моделей является возможность закраски каждой из граней объекта в соответствии с её освещенностью. Интенсивность освещенности произвольной точки пространства вычисляется по формуле:

, (3.3)

где Ip - интенсивность освещенности в точке,

Ка- коэффициент отражения;

Kd- коэффициент рассеивания;

I- интенсивность источника света;

n- единичная нормаль к грани, содержащей точку;

l- единичный вектор от точки к источнику света.

Каждый подход предусматривает определённый уровень реалистичности изображения. С повышением реалистичности изображения скорость алгоритма падает. Ниже будет рассмотрен один метод затенения объектов: плоское затенение.

Это простейший способ затенения. Для произвольной точки грани вычисляется интенсивность по формуле (3.3) и считается, что для всех точек грани интенсивность одинакова. В качестве точки для вычисления интенсивности не желательно брать граничные точки грани. Изображение носит явный полигональный характер.