4 Описание геометрических моделей объектов

4.1 Геометрическая модель куба

Куб задаётся единственным параметром w –длина ребра и состоит из восьми вершин: A11, A12, A13, A14 – вершины нижнего основания и A21, A22, A23, A24 – вершины верхнего основания. Пусть начало локальной системы координат куба совпадает с его геометрическим центром. Тогда координаты его вершин будут вычисляться следующим образом:

A11=(-w/2, -w/2, -w/2);

A12=(-w/2, -w/2, w/2);

A13=(w/2, -w/2, w/2);

A14=(w/2, -w/2, -w/2);

A21=(-w/2, w/2, -w/2);

A22=(-w/2, w/2, w/2);

A23=(w/2, w/2, w/2);

A24=(w/2, w/2, -w/2);

Геометрическая модель куба представлена на рисунке 4.1.

Рисунок 4.1 – Геометрическая модель куба

4.2 Геометрическая модель сферы

В графической базе данных сфера представляется тройкой вида (r, m, n), где r – радиус сферы, m – количество разбиений на вертикальной полуокружности при построении 0-го меридиана (тот на котором расположены точки на рисунке), n – количество разбиений на горизонтальной окружности при построении каждой из параллелей. Центр локальной системы координат связывается с геометрическим центром сферы. Изображение сферы приведено на рисунке 4.2.

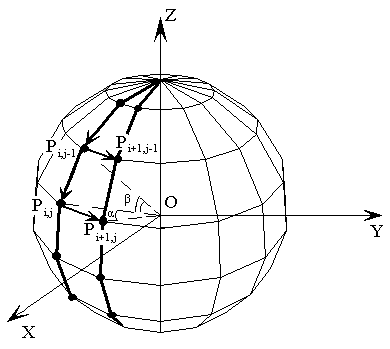
Рисунок 4.2 - Геометрическая модель сферы

Для построения сферы необходимо проделать следующие шаги.

1. Построить точку с координатами (0, 0, r) в локальной системе координат сферы.

2. Построить 0-вой меридиан. Каждая i-я точка 0-го меридиана получается из предыдущей методом вращения вокруг оси Х. Угол поворота точки при построении 0-го меридиана определяется как π/m. Координата следующей точки определяется по формуле:

P_i=P_i-1*ПоворотOX(π/m). (4.1)

Параллели получаются вращением 0-го меридиана вокруг оси OZ на угол 2π/n. Каждый следующий меридиан получается из предыдущего по формуле:

M_i=M_i-1*ПоворотOZ(π/n). (4.2)

4.3 Геометрическая модель полусферы

Для построения геометрической модели полусферы, необходимо учесть 3 параметра: количество разбиений по ширине (m), количество разбиений по высоте (n) и радиус сферы (r). Пусть основание полусферы лежит в плоскости XOZ, а часть полусферы без основания – со стороны положительного направления оси OY.

Для аппроксимации полусферы, необходимо построить n ломаных, состоящих из m точек.

Первая точка первой ломаной имеет координаты a11(0, r, 0), координаты остальных m-1 точек будем находить по формуле:

A_ij+1=A_ij*ПоворотOZ(-180/(m-1)). (4.3)

Координаты точек i-ой ломаной будем вычислять по формуле:

A_i+1j=Aij*ПоворотOY(-180/(n-1)). (4.4)

Геометрическая модель полусферы приведена на рисунке 4.3.

Рисунок 4.3 – Геометрическая модель полусферы

4.4 Геометрическая модель треугольной косоугольной призмы

Данный объект задаётся тремя параметрами: высота, радиус окружности, в которую вписано основание, смещение верхнего основания относительно нижнего вдоль оси OX. Обозначим эти параметры соответственно буквами h, r и s.

Пусть центр нижнего основания совпадает с началом локальной системы координат, а часть призмы без основания находится со стороны положительного направления оси OZ. Первая точка нижнего основания имеет координаты A11=(0, r, 0). Тогда координаты остальных точек нижнего снования будем находить по следующей формуле:

A_1i+1= A_1i*ПоворотOZ(360/3), (4.5)

а координаты точек нижнего основания – по формуле:

A_2i+1= A_2i*ПоворотOZ(360/3)*Перемещение(s, 0, h). (4.6)

Вид геометрической модели треугольной косоугольной призмы приведен на рисунке 4.4.

Рисунок 4.4 – Геометрическая модель треугольной косоугольной призмы

4.5 Геометрическая модель призмы с треугольным основанием

Данный объект задаётся двумя параметрами: высота и радиус окружности, в которую вписано основание. Обозначим эти параметры соответственно буквами h и r.

Пусть центр нижнего основания совпадает с началом локальной системы координат, а часть призмы без основания находится со стороны положительного направления оси OZ. Первая точка нижнего основания имеет координаты A₁₁=(0, r, 0). Тогда координаты остальных точек нижнего снования будем находить по следующей формуле:

A_1i+1= A_1i*ПоворотOZ(360/3), (4.7)

а координаты точек верхнего основания – по формуле:

A_2i+1= A_2i*ПоворотOZ(360/3)*Перемещение(0, 0, h). (4.8)

Вид геометрической модели призмы с треугольным основанием приведен на рисунке 4.5.

Рисунок 4.5 – Геометрическая модель призмы с треугольным основанием