
- •Кафедра теории металлургических процессов
- •1.2. Основные свойства кристаллического вещества
- •1.3. Распространённость кристаллических веществ
- •1.4. Пространственная решётка
- •1.5. Закон Бравэ
- •2. Симметрия кристаллов
- •2.1. Элементы симметрии
- •2.2. Плоскости симметрии
- •2.3. Центр инверсии
- •2.4. Оси симметрии
- •2.5. Инверсионные оси симметрии
- •2.6. Сложение элементов симметрии
- •2.7. Классификация видов симметрии
- •2.7.1 Сингонии низшей категории.
- •2.7.2Сингонии средней категории.
- •2.7.3Сингонии высшей категории.
- •3. Стереографические проекции
- •4. Учение о кристаллографических символах
- •4.1. Закон рациональности двойных отношений (закон Аюи)
- •4.2. Символы граней
- •4.3. Установка кристаллов
- •4.4. Индексы плоских сеток
- •5. Симетрия пространственных решёток
- •Трансляционные решётки
- •Часть вторая минералогия
- •Предмет и задачи современной минералогии, как науки
- •Процессы образования минералов в природе
- •3. Свойства минералов
- •3.1. Твердость
- •3.2. Спайность и излом
- •3.3. Плотность
- •3.4. Цвет минерала и цвет его черты
- •3.5. Блеск
- •3.6. Химический состав
- •3.7. Другие диагностические свойства минералов
- •4. Классификация минералов
- •4.1. Самородные элементы
- •4.2. Сульфиды
- •4.3. Галоидные соединения
- •4.4. Оксиды
- •4.5. Карбонаты, сульфаты, вольфраматы, фосфаты
- •4.6. Силикаты и алюмосиликаты
- •4.7. Характеристика горных пород
- •Список использованных источников
- •Содержание
2.5. Инверсионные оси симметрии
Инверсионные оси симметрии, обозначаемые буквой Li, являются сложными элементами симметрии. Они представляют собой как бы совокупность совместно действующих оси симметрии и центра инверсии.
Инверсионной осью симметрии называется прямая линия, при повороте вокруг которой на некоторый определенный угол с последующим отражением в центральной точке фигуры, как в центре инверсии, фигура совмещается сама с собой.
Симметричное преобразование, отвечающее инверсионной оси, состоит из поворота вокруг прямой линии и последующей инверсии в точке, лежащей на этой линии.
Рассмотрим пример инверсионной оси в правильной треугольной призме на рис. 2.10. В этой фигуре прямая gg является осью симметрии третьего порядка L3 и одновременно инверсионной осью шестого порядка. Действительно после поворота вокруг этой оси на 60° всех частей многогранника и последующего их отражения в центральной точке фигура самосовмещается.
Например, ребро АВ в результате поворота вокруг gg на 60° займет положение А1В1, а после отражения в центральной точке фигуры совместится с ребром А1В1. При полном повороте на 360° будет всего шесть таких совмещений. Следовательно, прямая gg представляет собой инверсионную ось шестого порядка Li6.
В кристаллических многогранниках возможны инверсионные оси первого, второго, третьего, четвертого и шестого порядка, т.е. Li1, Li2, Li3, Li4, Li6.
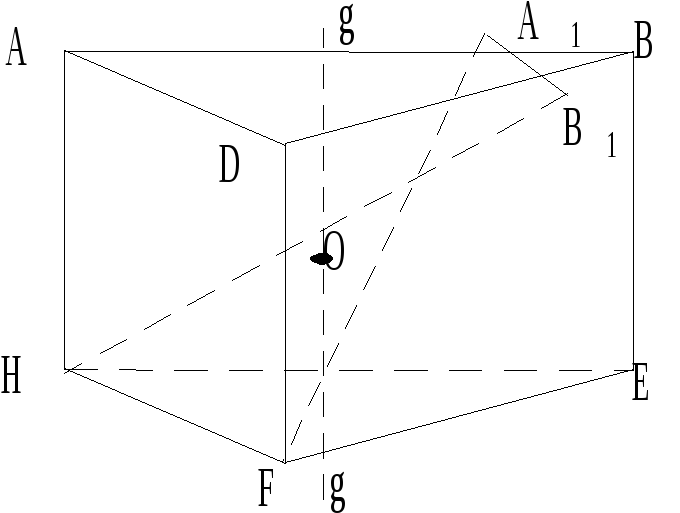
Рис.
2.10. Многогранник с инверсионной осью
шестого порядка
Инверсионная ось второго порядка по своему действию равнозначна перпендикулярной к ней плоскости симметрии, т. е. Li2=Р.
Инверсионная ось третьего порядка Li3 равносильна одновременно действующим оси симметрии третьего порядка L3, совпадающей с Li3 и центру инверсии С, т. е. , Li3=L3С. Так, например, в кубе, где присутствует совместно С и L3, каждая из четырех осей симметрии третьего порядка является в то же время тройной инверсионной осью. Наличие Li3, всегда совпадающей с простой осью симметрии третьего порядка, обычно не указывается.
Инверсионная ось четвертого порядка Li4 является самостоятельным элементом симметрии и не может быть ничем заменена. В многогранниках, обладающих Li4, центр инверсии отсутствует. Четвертая инверсионная ось всегда является одновременно осью симметрии второго порядка (Li4=L2), однако не любая двойная ось при отсутствии С отвечает Li4.
Инверсионная ось шестого порядка Li6 может быть заменена осью симметрии третьего порядка, совпадающей с Li6 и перпендикулярной к ней плоскостью симметрии:
Li6=L3P(P L3)
Кристаллические многогранники, обладающие Li6, самостоятельного центра инверсии не имеют.
Хотя Li6 можно заменить другими элементами симметрии, ею приходится пользоваться при классификации кристаллов, поэтому она упоминается наряду с Li4.
