2. Симметрия кристаллов

2.1. Элементы симметрии

Симметрия - широко распространенное в природе явление. Особенно многообразно симметрия проявляется в мире животных и растений. Кристаллы - наиболее яркие представители симметричных тел неживой природы.

Всякая симметричная фигура состоит из закономерно повторяющихся равных частей (рис. 2.1).

Вспомогательные геометрические образы, с помощью которых обнаруживается закономерная повторяемость равных частей фигуры, называются элементами симметрии.

Рис. 9. Пример симметричной фигуры

Операция совмещения частей симметричной фигуры и фигуры в целом называется симметрическим преобразованием.

Каждому элементу отвечает своё симметрическое преобразование, посредством которого фигура совмещается сама с собой.

В кристаллических многогранниках возможны элементы симметрии: плоскости симметрии, центр инверсии, оси симметрии и инверсионные оси.

2.2. Плоскости симметрии

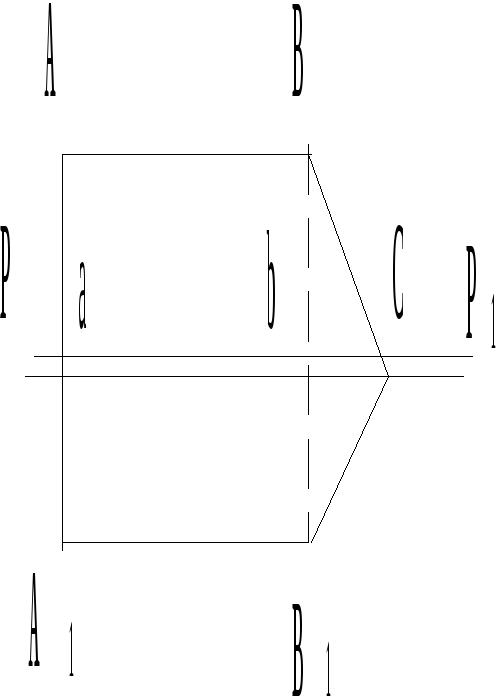
Плоскостью симметрии называется плоскость, которая делит фигуру на две равные части, расположенные друг относительно друга как предмет и его зеркальное отражение.

Плоскость симметрии обозначается буквой Р.

Симметрическое преобразование, отвечающее плоскости симметрии, есть отражение в плоскости.

Рис. 2.2. Фигура несимметричная

Для отражения некоторой фигуры АВD в плоскости Р (рис.2.3) из каждой её точки опускают перпендикуляры на плоскость отражения и продолжают их по другую сторону плоскости на расстояния, равные расстояниям отражаемых точек до плоскости Р. В результате получаем новую фигуру А₁В₁D₁.

Рис. 2.3. Отражение точек фигуры в плоскости Р

При нахождении плоскостей симметрии мысленно рассекают их плоскостью на две половины так, чтобы при отражении в этой плоскости половинки совместились друг с другом.

Не каждая плоскость, делящая фигуру пополам, является плоскостью симметрии. Например, в прямоугольнике только две плоскости параллельные его сторонам являются плоскостями симметрии (рис. 2.4). Плоскости идущие вдоль диагоналей прямоугольника плоскостями симметрии не являются, т. к. образующиеся треугольники зеркально не равны.

Рис.2.4. Прямоугольник АВDЕ имеет две плоскости (Р и Р₁) симметрии

Кристаллические многогранники могут иметь одну или несколько плоскостей симметрии. Число плоскостей симметрии указывается коэффициентом, стоящим перед буквой Р. Например, куб имеет 9Р, т. е. девять плоскостей симметрии (рис. 2.5).

Следует помнить, что плоскости симметрии или перпендикулярны к рёбрам и граням многогранника и проходят через их середины, или проходят вдоль рёбер.

2.3. Центр инверсии

Центром инверсии называется такая точка внутри фигуры, при отражении в которой всех точек последняя совмещается сама с собой.

Чтобы произвести отражение какой-либо точки фигуры в центре инверсии (рис. 2.6), нужно соединить эту точку и точку С прямой линией.

Как видно из рис. 2.6 плоскости треугольников параллельны, но стороны имеют противоположные

направления.

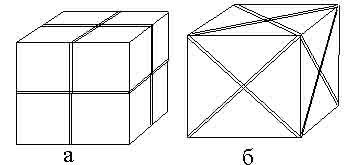
Рис. 2.5. Куб имеет девять плоскостей симметрии (9Р): три главных плоскости (а) и шесть диагональных (б)

Центр инверсии называют центром обратного равенства, потому что каждая грань при наличие центра инверсии должна иметь равную себе и обратно параллельную грань (рис. 2.7).

Рис. 2.6. Треугольник АВD и А₁В₁D₁, связанные центром инверсии, равны друг другу и обратно параллельны

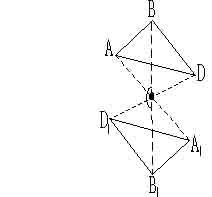
Рис. 2.7. Многогранник с центром инверсии С: грани попарно равны и обратно параллельны

Рис. 2.8. Многогранник не имеет центра инверсии, т.к. для грани q нет парной параллельной грани