Способы покрытиятаблицы квайна

При первом способе выделяются простые импликанты, без которых невозможно представление функции. Их характерной особенностью является то, что некоторые конституенты принадлежат только им. Для приведеннолго примера такими импликантами являются 0х1 1х0.

Объединение этих импликант называется ядром покрытия. Если ядро покрытия не перекрывает все конституенты функции, то к нему добавляются дополнительные импликанты до полного покрытия. Все минимальные покрытия отыскиваются с помощью простого перебора.

Так для нашего примера: ядро покрытия покрывает конституенты

0х1 - 001 и 011

1х0 - 100 и 110

Констутиента 111 осталась непокрытой ,следовательно к ядру нужно добавить еще одну импликанту. При этом получаем 2 минимальных покрытия:

{0х1 , 1х0 , х11}

{0х1 , 1х0 , 11х}

Первому покрытию соответствует тупиковая форма

f = ₁М₃ + М₁₃ + М₂ М₃

а второму:

f = ₁ М₃ + М₁М₃ + М₁М₂

Такой способ образования минимальных покрытий для функций с большим числом переменных затруднен при применении.

Рассмотрим другой ,более эффективный способ.

Для этого каждую простую импликанту таблицы Квайна представим с помощью множества. При этом будем считать ,что для таблицы Квайна множество – малые латинские буквы.

	001	011	100	110	111
0x1	1	1				А
x11		1			1	В
1x0			1	1		С
11x				1	1	D

В этом случае конституенты покрываются следующими множествами.

001 – P₁=a

011 – P₃=a+b

100 – P₄=c

110 – P₆=c+d

111 – P₇=b+d

Из этого следует, что все возможные минимальные покрытия представляются множествам Р равным:

Р = а( а + b ) с ( с + d )( b + d)

Применяя, рассмотренные ранее, законы для операций над множествами:

Р = а( а + b ) c ( c + d )( b + d ) = ac ( b + d ) = acb + acd

acb – { 0x1, 1x0, x11 }

acd – { 0x1, 1x0, 11x }

f ₁ = ₁M₂ + M₁₃ + M₂M₃

f ₂ = ₁M₂ + M₁₃ + M₁M₂

Рассмотрим более сложный пример .

Функция от четырех переменных:

Kj	F
0000	0
0001	0
0010	0
0011	1
0100	1
0101	1
0110	0
0111	1
1000	0
1001	1
1010	0
1011	1
1100	1
1101	1
1110	0
1111	0

Выпишем все образующие функцию конституенты, разбив на классы по количеству единиц.

0100 010x

0011 x100

0101 0x11

1001 x011

1100 01x1

0111 x101

1011 10x1

1101 1x01

110x

Объединяя их, получим: х10х х10х

	0100	0011	0101	1001	1100	0111	1011	1101
x10x	1		1		1			1	A
0x11		1				1			B
x011		1					1		C
01x1			1			1			D
10x1				1			1		E
1x01				1				1	F

f ₁ = M₂₃ + ₁M₃M₄ + M₁₂M₄

f ₂ = M₂₃ + ₁M₃M₄ + ₂M₃ М₄ + M₁₃M₄

f ₃ = M₂₃ + ₂M₃M₄ + ₁М₂ М₄ + M₁₂M₄

f ₄ = M₂₃ + ₂M₃M₄ + ₁М₂ М₄ + M₁₃M₄

Получены тупиковые формы. Их сложность соответственно:

S₁ = 8, S₂ = 11, S₃ = 11, S₄ = 11

Следовательно имеем одну минимизированную форму f₁

P = a(b+c)(a+d)(e+f)a(b+d)(c+e)(a+f) = a(b+c)(e+f)(b+d)(c+e) = a(b+cd)(e+cf) =

(ab+acd)(e+cf) = abe + abcf + acde + acdf

БУЛЕВА АЛГЕБРА

Алгебра – это множество М, с заданными на нем функциями, обладающими свойствами замкнутости.

f (m_i)  M_i ; m_i  M.

Алгебра – некоторое множество М , с определенными на этом множестве операциями. Все функции ,заданные на М ,обозначаются буквой S –сигнатура алгебры. Множество М – носитель алгебры. Произв. алгебра А обозначается:

А < М, S >

ФУНДАМЕНТАЛЬНЫЕ АЛГЕБРЫ.

1. Алгебра А = < М , f₀ > ,где f₀ - двуместная функция, называется группой. При этом f : a , b  с , c = ab - обобщенное умножение

С обладает свойствами:

- если (а,b  М, то результат обобщенного умножения так же принадлежит М

[(ab)  M]

Это свойство замкнутости;

- (ab)c = a(bc) - свойство ассоциативности

- (ax) = b , ya = c - существованиеединственного решения уравнения

Группа , для которой выполнено условие:

ab = ba

называется коммутативной или абелевой группой.

ПРИМЕРЫ АЛГЕБРАИЧЕСКИХ СИСТЕМ

N - множество натуральных чисел

R - множество целых чисел

Z - множество действительных чисел

Определим алгебру вида:

А = < N, + , * , - >

Эта алгебра не является алгебраической системой

А = < N < + , * , > - алгебраическая система

Причем в данном примере содержится алфавит из бесконечного числа элементов.

Существуют алгебры с конечным алфавитом. Примером такой алгебры есть алгебра подстановок.

Образовывающаяся алгебра подстановок с помощью перестановок 3-х элементов х₁, х₂,х₃ .

Отметим возможные варианты.

1	x1	x2	x3
2	x1	x3	x2
3	x3	x2	x1
4	x2	x1	x3
5	x2	x3	x1
6	x3	x1	x2

Элементы носителя определяются следующим образом

a = x₁ x₂ x₃ b = x₁ x₂ x₃ c = x₁ x₂ x₃

x₁ x₂ x₃ x₁ x₃ x₂ x₂ x₁ x₃

d = x₁ x₂ x₃ e = x₁ x₂ x₃ c = x₁ x₂ x₃

x₂ x₃ x₁ x₃ x₁ x₂ x₃ x₂ x₁

Например элемент b означает,

что х₁ переходит в х₁

х₂ переходит в х₃

х₃ переходит в х₂

Определим групповую операцию, как общий переход:

bc = x₁ x₂ x₃ x₁ x₂ x₃ = x₁ x₂ x₃ = d

x₁ x₃ x₂ x₂ x₁ x₃ x₂ x₃ x₁

Составим мультипликативную таблицу:

	a	b	c	d	e	f
a	a	b	c	d	e	f
b	c	a	d	c	f	e
c	c	e	a	f	b	d
d	d	f	b	e	a	c
e	e	c	f	a	d	b
f	f	d	e	b	c	a

Проверим выполняется ли закон ассоциативности для данного примера:

(bd)f = cf =d

b(df) = bc =d

то есть, закон выполняется.

Так же можно показать, что закон справедлив для любых элементов данной алгебры .Видно, что алгебра замкнута, но не выполнено свойство коммутативности.

Поэтому алгебра – мультипликативная некоммутативная группа.

Алгебра вида

А = < М , * , + >

Называется кольцом, если < М , + > есть аддитивная абелевая группа, выполняется закон дистрибутивности.

Если операция обобщ. умн. кольца < М, * > содержит 1, то имеет место кольцо с единицей.

Если умн. коммут. то кольцо – коммутат. Полем называется кольцо с единицей, ненулевые элементы которого образуют группу по умножению. Если эта группа имеет конечное число элементов и является абелевой, то такие поля называются полями Галуа.

Рассмотрим примеры :

1.Множество действительных чисел с опер. слож. и умноженные есть коммутативное поле.

2. Алгебра вида :

А = < М, ₀ , + > ,где М {0,1,2,3,4,5} ₀ , + по модулю 6.

Составим таблицу умножения и сложения.

с = а + в mod 6

+	0	1	2	3	4	5
0	0	1	2	3	4	5
1	1	2	3	4	5	0
2	2	3	4	5	0	1
3	3	4	5	0	1	2
4	4	5	0	1	2	3
5	5	0	1	2	3	4

с = ав mod 6

*	0	1	2	3	4	5
0	0	0	0	0	0	0
1	0	1	2	3	4	5
2	0	2	4	0	2	4
3	0	3	0	3	0	3
4	0	4	2	0	4	2
5	0	5	4	3	2	1

Из таблиц видно, что эта алгебра есть коммут. кольцо с 1.

3. А = < М, ₀ , + > М{0,1,2,3,4,5,6} c = a + b mod 7

+	0	1	2	3	4	5	6
0	0	1	2	3	4	5	6
1	1	2	3	4	5	6	0
2	2	3	4	5	6	0	1
3	3	4	5	6	0	1	2
4	4	5	6	0	1	2	3
5	5	6	0	1	2	3	4
6	6	0	1	2	3	4	5

*	0	1	2	3	4	5	6
0	0	0	0	0	0	0	0
1	0	1	2	3	4	5	6
2	0	2	4	6	1	3	5
3	0	3	6	2	5	1	4
4	0	4	1	5	2	6	3
5	0	5	3	1	6	4	2
6	0	6	5	4	3	2	1

Для данного алфавита можно определить и обратную операцию вычитания.

а – в = а(-в)

Для данной алгебры составленна таблица :

а	-а
0	0
1	6
2	5
3	4
4	3
5	2
6	1

По аналогии составляется таблица обратных элементов для деления.

1^-1=1; 2^-1=4; 3^-1=5; 4^-1=2; 5^-1=3; 6^-1=6;

Вышепреведенные алгебры являются полем Галуа.

СИСТЕМЫ УРАВНЕНИЙ И ПОЛЯ ГАЛУА.

Как и в обычной алгебре можно решать системы уравнений и в полях Галуа.Возьмем следующую систему :

X₁+3x₂+6x₃=2

4x₁+5x₂+2x₃=1

2x₂+x₃=5

Будем решать систему по методу Гаусса :

1 3 6

= 4 5 2 mod 7 = (5+48–4–12) mod 7=37 mod 7 = 2

0 2 1

2 3 6

₁ = 1 5 2 mod 7 = (–109) mod 7=(140-109) mod 7 = 31 mod 7 = 3

0 2 1

₂ = 103 mod 7 = 5 ₃ = (27-21) mod 7 = 0

x₁=3*2^-1=3*4=5

x₂=5*2^-1=5*4=6

x₁=0*2^-1=0*4=

5+3*6+6*=5+4+=2+=2

4*5+5*6=6+2=1

2*6=5

БУЛЕВЫ АЛГЕБРЫ.

Изоморфизмом между алгебрами называется взаимооднозначное соответствие между носителями и сигнатурами.

f_i(x₁,…x_n)=x_k   (f_i)[ (x₁),… (x_n)] =  (x_k)

Алгебры для которых существует изоморфизм  называют изоморф-ми.

Очевидно, что законы справедливые для некоторой алгебры , также будут справедливы и для изоморфной с ней алгебры.

Булевы алгебры – алгебры вида :

A = < M, + , * , - > для которых справедливы следующие отношения :

 х_i  M

1. x_i + x_j = x_j + x_i

2. x_i * x_j = x_j * x_i

3. (x_i + x_j) + x_k = x_i + (x_j +x_k)

4. (x_i * x_j) * x_k = x_i * (x_j *x_k)

5. (x_i + x_j) * x_k = x_i *x_k+ x_j*x_k

6. x_i + x_j * x_k = (x_i + x_j)(x_i+x_k)

7. x_i+x_j  M, x_i x_j  M

8. x  = x; x = ; x + E = E; x +  = x;

9. x * = E; x *=;

Множество вида М = {I_j, E, }

I_j – интервалы пораждающих множеств;

E – единичное множество;

 - пустое множество;

и определенные на нем операции +, *, - есть булева алгебра или алгебра множеств. Булевы алгебры есть частный случай фундаментальных видов алгебр.

АЛГЕБРА БУЛЯ.

Булевой переменной является переменная, которая принимает значение 0 или 1. Будем обозначать такую переменную Х. Если в некоторой алгебре Буля определены функции от к переменных, то будем называть её к-значной, а сигнатуру обозначать как Р_к .

Операция обобщ-го сложения в случае булевых алгебр называют дизъюнкцией, а операция обобщ-го умножения – конъюкцией.

Групповая операция обобщ. сложения :

х₁х₂ ~ x₁ + x₂

Операция обобщенного умножения :

x₁&x₂

0 0 = 0 0 & 0 = 0

0 1 = 1 0 & 1 = 0

1 0 = 1 1 & 0 = 0

1 1 = 1 1 & 1 = 1

Установим выполдняется ли для данной алгебры законы теории множеств :

1. Дистрибутивный закон

х₁(х₂х₃)=х₁х₂х₁х₃

Составим таблицу :

x1	x2	x3	х1(х2х3)	х1х2х1х3
0	0	0	0	0
0	0	1	0	0
0	1	0	0	0
0	1	1	0	0
1	0	0	0	0
1	0	1	1	1
1	1	0	1	1
1	1	1	1	1

1^-йзакон дистрибутивности применим к алгебре Буля. Аналогичная таблица для 2^-гозакона дистрибутивности.

(х₁х₂)(х₁х₃) = x₁(x₂ & x₃)

x1	x2	x3	(х1х2)(х1х3)	x1(x2 & x3)
0	0	0	0	0
0	0	1	0	0
0	1	0	0	0
0	1	1	1	1
1	0	0	1	1
1	0	1	1	1
1	1	0	1	1
1	1	1	1	1

2. Проверим закон де Моргана.

Отрицание конъюкции есть дизъюнкция отрицания.

₁& ₂ = ₁₂

x1	x2	1& 2	12
0	0	1	1
0	1	1	1
1	0	1	1
1	1	0	0

Отрицание дизъюнкции равно конъюкции отрицания.

₁₂ = ₁&₂

x1	x2	12	1&2
0	0	1	1
0	1	0	0
1	0	0	0
1	1	0	0

Первый и второй законы де Моргана применимы для алгебры Буля.

ПРИОРИТЕТЫ АЛГЕБРЫ БУЛЯ.

1. –

2. &

3. 

4. 

ОСНОВНЫЕ ОПЕРАЦИИ АЛГЕБРЫ БУЛЯ.

(АЛГЕБРЫ ЛОГИКИ).

ТАБЛИЦЫ ИСТИННОСТИ ЭТИХ ОПЕРАЦИЙ.

1. « НЕ » - х

0 1

1 0

2. х₁х₂ « ИЛИ »

х1 х2	х1х2
0 0	0
0 1	1
1 0	1
1 1	1

3. Конъюкция х₁& х₂ « И »

х1 х2	х1& х2
0 0	0
0 1	0
1 0	0
1 1	1

4. Импликация х₁х₂« ЕСЛИ ТО »

х1 х2	х1х2
0 0	1
0 1	1
1 0	0
1 1	1

5. Эквиваленция х₁ ~ х₂« ТОГДА И ТОЛЬКО ТОГДА »

х1 х2	х1 ~х2
0 0	1
0 1	0
1 0	0
1 1	1

ПРЕДСТАВЛЕНИЕ ФУНКЦИИ В АЛГЕБРЕ БУЛЯ.

Функция трех переменных :

x1	x2	x3	f
0	0	0	1
0	0	1	0
0	1	0	1
0	1	1	1
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	0

Кроме табличного задания алгебры логики применяются различные аналитические методы. К ним относятся – дизъюктивная и коньюктивная форма. Для представления в дизъюктивной соверш. норм. форме (ДСНФ) вводится фар-кая функция единицы, которая соответствует конституентам, в которых функция принимает значение = 1.

Единичная функция записывается ,как элементарная конъюнкция, содержащая n – переменных и называется минитермом. Алгоритм представления функции алгебры логики в виде ДСНФ записывается в виде:

1. Выбрать в таблице функции все наборы аргументов , на которых функция обращ. в единицу

2. Вычислить конъюкцию, соответствующей этим наборам аргументам. При этом аргумент x_i входит в данный набор как 1 , он вписывается без изменения в конъюнкцию, соответствующую данному набору. Если х_i входит как 0 ,то в конъюнкцию вписывается его отриц.

3. Все полученные конъюнкции соединены между собой знаками дизъюнкции.

Для примера запишем ДСНФ

f(х₁,х₂, х₃) = _{1 2 3 1} x_{2 3 1 2} x₃ x_{1 2 3} x_{1 2} x₃

x₁ x_{2 3}

Для представления функции алгебры логики в КСНФ вводится хар-кая

функция О ,которая соответствует набору, на котором функция принимает значение О. Функция нуля записывается как элементарная дизъюнкция, содержащая n-переменных и называется макситермом.

Алгоритм построения КСНФ:

1. Выбрать в таблице функции все наборы аргументов , на которых функция обращается в О.

2. Выписать дизъюнкции, соответствующие этим наборам. При этом если х_i входит как О, он вписывается без изменений в дизъюнкцию, если х_i входит как 1, то в дизъюнкцию вписывается его отрицание.

Для примера запишем КНФ

f(х₁,х₂, х₃) = (x₁ x₂₃ ) & (_{12 3})

По аналогии с теорией множеств при минимизации:

ДСНФ  ДНФ

КСНФ  КНФ

ДНФ,КНФ – обозначения для сокращения макситермами и минитермами. Номера мини- и макситермов являются дес-ными экв-ми соответствующего набора, на котором функция принимает 1 или 0 соответственно, то есть

(ДСНФ) f( х₁,х₂,х₃ ) = m₀ m₂ m₃ m₄ m₅ m₆

(КСНФ) f( х₁,х₂,х₃ ) = m₁ & m₇

Согласно теореме Шеннона функция в ДСНФ имеет вид :

f( х₁,…,х_k) = f( ₁,…,_k)& x₁^1* x₂^2… x_k^k

Функция трех переменных задана таблично :

x1	x2	x3	f
0	0	0	1
0	0	1	0
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	0
1	1	1	1

f(х₁,х₂, х₃) = _{1 2 3 1} x_{2 3 1}x₂ x₃ x₁ x₂ x₃ (ДСНФ)

Выясним каково количество возможных булевых функций к-значных.

Если мы имеем к переменных, то из них можно составить m=2^к комбинаций, а так как для каждой комбинации может быть задана своя функция, то общее число возможных функций V=2^m=2^{2^k}

Теорема :

Алгебра множеств с к-порожденными множествами изоморфна к-значной алгебре Буля.

Доказательство:

Изоморфизм строится следующим образом:

 (М_i)=x_i - для алгебры множеств

 (f_i)=y_i - для алгебры Буля

Тогда согласно представлению Булевых функций в ДСНФ и представлению функций от порождающих множеств в СНФК следует следующее :

f_j(M_i) = M_v^v ;

y_j(x_i) = x_v^v ;

Основным следствием этой теоремы является возможность применения всех методов минимизации из теории множеств для алгебры Буля.

Метод Квайна для функции Буля :

0 0 0

0 1 0 0х0

0 1 1 х11

1 1 1

Строим таблицу Квайна :

	000	010	011	111
0х0	1	1
х11			1	1

Y(x₁, x₂, x₃) = ₁₃x₂x₃

Минимизация по методу Карно :

х1 х2х3	00	01	11	10
0	1		1	1
1			1

f(x₁, x₂, x₃) = ₁₃x₂x₃

ФУНКЦИОНАЛЬНО ПОЛНЫЕ СИСТЕМЫ ФУНКЦИЙ.

Запишем таблицу функций 1-й перем.:

x	y1	y2	y3	y4
0	0	0	1	1
1	0	1	0	1

y₁ – функция константы О ;

y₂ – переменная х ;

y₃ – отриц. переменная х ;

y₄ – конст-ты 1.

Для алгебры с двузначной логикой составим аналогичную таблицу всех возможных функций.

х1	х2	F0	F1	F2	F3	F4	F5	F6	F7	F8	F9	F10	F11	F12	F13	F14	F15
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

Некоторые из этих функций встречались ранее :

F₁(x₁, x₂) = x₁ * x₂ - дизъюнкция

F₆(x₁, x₂) = x₁  x₂ - слож. по модулю 2

F₇(x₁, x₂) = x₁ x₂ - конъюкция

Сведем в таблицу :

Функция	Название	Предназначение
F0	конст-та 0	
F1	конъюкция	Логич. умнож. х1х2
F2	отрицание по х2	х1 2
F3	повт-ль х1	х1
F4	запрещение по х1	1х2
F5	повт-ль х2	х 2
F6	сумма по mod 2	х1х2
F7	дизъюнкция	логич. сложен. х1х2
F8	стрелка Пирса	х1  х2
F9	эквив-ти	х1 ~х2
F10	отрицание х2	2
F11	импликация по х2	х2x1
F12	отрицание х1	1
F13	импликация по х1	x1  х2
F14	отр. конъюкции	1 2
F15	конст-та 1	1

Функционально-полной системой алгебры Буля – набор функций Р_к, с помощью которых может быть выраженна любая функция из Р_к.

Тривиальной функционально-полной системой является весь набор функций из Р_к.

Базисом алгебры Буля называется функционально-полная система, которая перестает быть таковой при выбрасывании из неё любой функции.

Примером алгебры с функционально-полной системой, но не являющейся базисом является функция вида :

А = < M, , &, - >

На основании законов де Моргана из неё можно получить алгебры с базисами.

А₁ = < M, , - > ,А₂ = < M, &, - >

Принцип нахождения функционально-полных систем и базисов для Р_к .

Будем искать такой набор из Р_к, с помощью которого можно представить функции дезъюнкции, конъюкции, отрицания, а следовательно и все остальные функции. Для изучения свойств пространства Р₂ , т. е. Функция от двух переменных, представим все функции с помощью операций дезъюнкции, конъюкции и отрицания.

F1 = х1*х2

F2 = х1*2

F4 = 1*х2

F6 = х1х2 = 1*х2х1*2

F7 = х1 х2

F8 = 1*2 = 12

F9 = 12 х1х2 = х1х2

F10 = 2

F11 = 12 х12 х1х2 = x12

F12 = 1

F₁₃ = _{12 1}х₂ х₁х₂ = ₁ х₂

F₁₄ = _{12 1}х₂ х₁₂ = _{1 2} = ₁₂

Для каждой из перечисленных функций существует двух ходовой логический элемент.

Изобразим эти элементы.

F₁ = x₁x₂ F₂ = x₁₂ F₄ = ₁x₂

x₁ x₁ x₁

x₂ & y₁ x₂ & y₂ x₂ & y₄

F₆ = х₁х₂ F₇ = х₁ х₂ F₈ = ₁₂

x₁ x₁ x₁

x₂ y₆ x₂ 1 y₇ x₂ 1 y₈

F₉ = х₁х₂ F₁₀ = ₂ F₁₁ = x₁₂

x₁ x₁ x₁

x₂ y₉ x₂ 1 y₁₀ x₂ 1 y₁₁

F₁₂ = ₁ F₁₃ =₁ х₂ F₁₄ = ₁₂

x₁ x₁ x₁

x₂ 1 y₁₂ x₂ 1 y₁₃ x₂ & y₁₄

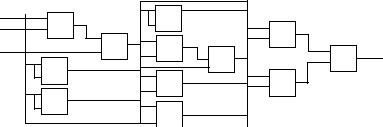
На основании этих элементов можно синтезировать любую логическую функцию.

f(х₁,х₂,х₃) = х₁х₂х_{3 1}х₂ х_{1 2 123}

_{02 07}

^{x1 00 1}

^{x2 01 &} ₀₃ ⁰⁴ ₁₂

₀₄ ⁰⁵ ₀₉ ¹

^{x3 02 &} ₀₆ ^& _{08 09 1 14 f}

⁰⁰ ₁ ^{07 &}

⁰⁵ ₁₀ ¹⁰

₀₁ ^{01 &} ₁₁ ¹

¹ ₀₀

_& ¹¹

₀₆

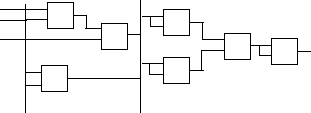
Реализуем функцию вида f(х₁,х₂,х₃):

f(х₁,х₂,х₃) = х₁₂х₃ & ₁х₃

^{x1 00} ₀₄

^{x2 01 &} _{03 04 1} ⁰⁶

_{x3 02 &} ⁰⁴

^& _{08 1} ^{f 09}

⁰⁵ ₀₇

_& ^{05 05 1}

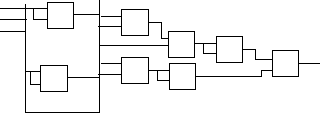
f(х₁,х₂,х₃) = х₁₂х_{3 1}х₃ = ₁ х₂₃x₁₃

_{x1 00 00}

_{x2 01 00} ^{1 03 03} _{1 05}

_{x3 02} ⁰¹

_{04 1 06}

₀₈

₀₂ ^{00 1 10 f}

_{02 1} ^{04 04 1} _{07 1} ⁰⁹

СВОЙСТВА БУЛЕВЫХ ФУНКЦИЙ.

Функциональным классом называется множество всех функций, обладающих определенным свойством.

Функциональный класс замкнутый,если суперпозиция этого класса принадлежит этому же классу.

Например, класс функций, полученных с помощью дизъюнкции аргументов замкнут.

y(x₁,x₂) = x₁x₂ ,где x₂(z₁,z₂) = z₁z₂

y(x₁,x₂(z₁,z₂)) = y(x₁,z₁,z₂) = x₁z₁z₂

Перечислим некоторые свойства. Для булевой функции определим понятие набора.

Набор – фиксируемое значение аргументов функции ,   = {0110}

Между различными наборами установим соотн. сравнения:

₁ > ₂ , если любой элемент набора ₁  соответственно элементу из набора ₂

₁ = (11010)

₂ = (01010)  ₁ > ₂

₁ = (01001)

₂ = (10100)  2 набора несравнимы

 = (₁, ₂, …,_n)

 = (₁, ₂, …,_n) наборы знач. перем. знач. и считается  >  , если _i > _i

ТЕОРЕМА.

Если булева функция может быть представлена в нормальной дизъюктивной форме без отрицания, то эта функция монотонна.

ДОКАЗАТЕЛЬСТВО.

Возьмем произвольные значения  и , причем   . В этом случае условию теоремы удовлетворяют следующие возможности:

у(  ) = 0 , у (  ) = 0

у(  ) = 0 , у (  ) = 1

у(  ) = 1 , у (  ) = 1

Откуда следует, что для доказательства теоремы достаточно доказать следующее утверждение:

если   , то у (  ) = 1 у (  ) = 1

Докажем это утверждение.

Если у(  ) = 1, то всегда найдется интервал, для которого выполняется следующее условие:

x_j1, x_j2 … x_jk_ = 1, где _j1 = _j2 = _jk = 1

j - номер набора перем.без отрицания, тогда

_j1 = _j2 = _jk = 1  x_j1, x_j2 … x_jk_ = 1

значит у(  ) = 1

Следствием теоремы является замкнутость класса монотонных функций.

Например:

y(х₁,х₂,х₃) = х₁х₂ х₁х₃ х₂х₃ , где х₂(z₁,z₂) = z₁ z₂

тогда: y(x₁,x₂(z₁,z₂)x₃) = x₁(z₁ z₂) x₁x₃ x₃(z₁ z₂) =

= x₁z₁ x₂z₂ x₁x₃ x₃z₁ x₃z₂

Так как результирующая функция не содержит отрицания, то она является монотонной.

ЛИНЕЙНЫЕ ФУНКЦИИ И АЛГЕБРА ЖЕГАЛКИНА.

Алгебра Буля – частный случай булевых алгебр и кроме него существует бесконечное число булевых алгебр.Одна из них – алгебра Жегалкина.

Это к-значная алгебра вида: А = < М, , & >

Она подчиняется следующим законам:

х  у = у  х

х ( у  z ) = xy xz

х  х = Любую булеву функцию можно представить с помощью алгебры Жегалкина.

Например:

Операция отрицания:= х 1

Операция сложения: х + у = = (х 1 )(у  1)  1 = ху  х  у  1   1 = ху  х  у

следовательно, исходя из теоремы Шинона , через операции сложения поmod 2 (  ) и конъюнкции ( & ) может быть выражена любая функция.

f(х₁,х₂,х₃) = х₁₂х₃ +₁х₃ = x₂₁х₃ & ₁х₃ = (х₁х₃(х₂  1)  1) & (х₃(х₁  1))  1 =(х₁х₂х₃  х₁х₃  1)(х₁х₃  х₃  1)  1 = х₁х₂х₃  х₁х₂х₃  х₁х₂х₃  х₁х₃  х₁х₃  х₁х₃  х₁х₃  х₃  1  1 = х₁х₂х₃  х₃

Любая функция ,представленная с помощью алгебры Жегалкина, называется полиномом Жегалкина.

Функция линейная, если она представлена полиномом Жегалкина вида:

f(х₁,х₂,….х_n) = _i x_i + j

- сумма по модулю 2

_i - произв. коэффициент

j - свободный коэффициент

Класс линейных функций так же замкнут.

Пример: f(х₁,х₂,х₃) = х₁  х₃ ₁ = 1, ₂ = 0, ₃ = 1, j = 0

С помощью линейного полинома Жегалкина можно представить функцию отрицания: f(1,x₂.1) = g(x₂) = ₂

Полином Жегалкина через нелинейные функции содержит слагаемые, являющиеся произведением множителей из слагаемых выберем то, которое состоит из мин. числа сомножителей и обозначим К,

а слагаемые: x_j1,x_j2,…,x_jk

Предположим, что х_j1 и х _j2 принимают произвольные значения функции,

а x_j3 = x_j4 = …= x_jk = 1; a x_jk+1 = x_jk+2 = … = x_jk+n = 0

Тогда функция от аргументов имеет вид:

f (x₁,…,x_n) = x_j1x_j2  x_j1  x_j2  j

где , , j - произ. коэффициенты

Полином данного вида называется нелинейным полиномом Жегалкина.

Покажем, что при любых , , j для функции f_i (x_j1,x_j2) может быть получена конъюнкция (используем функцию отрицания q(x) = ).

Для этого составим таблицу, где для удобства обозначим: x_j1 = x ; x_j2 = y

f(x,y) = xy  x  y  j

fi	  j	& 	& —	xy
f0	0 0 0	xy	xy	f0(xy) = xy
f1	0 0 1	xy  1	xy	g(f1(xy)) = xy
f2	0 1 0	xy  y	y	f2(g(x),y) = xy
f3	0 1 1	xy  y  1	y	G(f3(g(x),y)) = xy
f4	1 0 0	xy  x	x	f4(x,g(y)) = xy
f5	1 0 1	xy  x  1	x	G(f5(x,g(y))) = xy
f6	1 1 0	xy  x  y		g(f6(g(x),g(y))) = xy
f7	1 1 1	xy  x  y  1		f7(g(x),g(y)) = xy

Таким образом с помощью суперпозиции нелинейных функции и функции отрицания можно получать функцию коньюнкции.

Пример: f(x₁,x₂,x₃) = x₁₂ + ₁x₃ + x₂

Преобразуем функцию в мин.форму, представив с помощью операции сложения по

mod 2 и конъюнкции

f(х₁,х₂,х₃) = x₁₂ & ₁x₃ & ₂ = ((х₁(х₂  1))  1)) & ((х₃(х₁  1)  1) & (х2  1)  1 = (х₁х₂  х₁  1)(х₁х₃  х₃  1)(х₂  1)  1 = (х₁х₂х₃  х₁х₂  х₁х₃  х₁  х₃  1)(х₂  1) = х₁х₂х₃  х₁х₂  х₂х₃  х₂  х₁х₃  х₁  х₃  1

Выберем в качестве мин. слагаемого х₁х₂х₃= 0

f(x₁,x₂,  ) = x₁x₂  x₁  x₂  1 = ₁₂

x₁x₂ = f(q(x₁),q(x₂),)

ФУНКЦИОНАЛЬНО – ПОЛНЫЕ СИСТЕМЫ И БАЗИСЫ В ШИРОКОМ

СМЫСЛЕ.

ФПС пространства Р_в широком смысле называется множество функций с помощью суперпозиции которых можно представить любую функцию из Р_, используя при этом конституенты 0 и 1.

Базисом Р_в широком смысле называется ФПС, из которого не может быть вычеркнута ни одна функция без потери полноты системы.

ТЕОРЕМА.

Система функции полная в широком смысле , если в ней присутствует хотя бы одна немонотонная и хотя бы одна нелинейная функция.

Доказательство:

Достоверность следует из того , что если в системе существует хотя бы одна немонотонная функция, то может быть представлена функция отрицания.

Если при этом есть нелинейная функция, то с помощью ее может быть представлена любая функция Р_.

Необходимость.

Если в системе все функции монотонны, то не может быть получена немонотонная функция, так как класс функций замкнут.

Следовательно, найдутся такие функции, которые не представимы суперпозиции функции системы, тоесть такая система не функционально-полная.

ПОСТРОЕНИЕ БАЗИСА Р_В ШИРОКОМ СМЫСЛЕ.

Составим следующую таблицу:

yi	Kн	Кл
y1		1	a
y2	1	1	b
y6	1		c
y7		1	d
y8	1	1	e
y9	1		f
y12	1		g
y13	1	1	h
y14	1	1	k

у₁= х₁х₂

у₂= х₁₂= х₁(х₂1) = х₁х₂х₁

у₆=₁х₂+ х₁₂= х₁х₂

у₇= х₁ + х₂= х₁х₂х₂+ х₂

у₈=₁₂= х₁х₂х₁х₂х₁

у₉= ₁₂+х₁х₂= х₁х₂1

у₁₂ =₁= х₁1

у₁₃=₁+ х₂= х₁х₂х₁1

у₁₄=₁+₂= х₁х₂1

Это сокращенная таблица Поста, служит для нахождения базисов в широко смысле пространства Р_.

Таблица заполняется по принципу:

-если данная функция не принадлежит данному классу ,то в соответствующей клетке ставится 1.

Для получения всех базисов в широком смысле пространства Р_нужно найти все мин. покрытия, удовлетворяющим полноты ,но теряющие это свойство при удалении любого элемента из покрытия. Для этого применим метод Квайна.

P = (b + c + e + f + q + h + k) &(a + b + d + e + h + k) = ((b + e + h + k) + c + f + q)

&((b + e + h + k) + a + d) = ( b + e + h + k) + (a + d)(b + e + h + k) + (c + f + q) *

*(b + e + h + k) + (c + f + q)(a + d)= b + e + h + k + ca + fa + fd + qa + qd

Получены 10 базисов в широком смысле пространства Р_.

В₁= {y₂} B₆= {y₆,y₇}

B₂= {y₈} B₇= {y₁,y₉}

B₃= {y₁₃} B₈= {y₇,y₉}

B₄= {y₁₄} B₉= {y₁,y₁₂}

B₅= {y₁,y₆} B₁₀= {y₇,y₁₂}

Используя любой из 10 указанных базисов в широком смысле, можно выразить произвольную булеву функцию.

ФУНКЦИОНАЛЬНО – ПОЛНЫЕ СИСТЕМЫ И БАЗИСЫ В УЗКОМ СМЫСЛЕ.

Функционально полной системой пр-ва Р_в узком смысле называется множество функции с помощью суперпозиций которых можно представить любую функцию пр-ва Р_, при этом 0 и 1 не используются.

Для построения базиса рассмотрим следующие классы функций :

• класс самодвойственных функций

Функция f от n аргументов называется самодвойственной если выполняется условие:

f (x₁, x₂, …, x_n) = (₁, ₂, …, _n)

Класс самодвойственных функций замкнут.

Для доказательства возьмем 2 самодвойственных функции, для которых выразим x через t и найдем их суперпозицию.

x₁ (t₁, t ₂, t₃) = ₁ ( ₁, ₂, ₃)

f(x₁ (t₁, t ₂, t₃), x₂, x₃) = d (t₁, t ₂, t₃, x₂, x₃) = (x₁ ( ₁, ₂, ₃), _{2, 3}) =

= (₁, ₂, ₃, _{2, 3})

На основании вышезаписанного делаем вывод, что класс самодвойственных функций замкнут.

• класс функций, сохраняющих 0

Функция f от n аргумента называется сохраняющей 0 если :

f (  , , …,  ) = 

Можно доказать, что и класс функций сохраняющих 0, замкнут.

• класс функций, сохраняющих 1

Функция f от n аргумента называется сохраняющей 1 если :

f ( 1 , 1, …, 1 ) = 1

Можно доказать, что и класс функций сохраняющих 1, замкнут.

ВТОРАЯ ТЕОРЕМА О ФУНКЦИОНАЛЬНОЙ ПОЛНОТЕ.

Система функций будет полной если она содержит хотя бы одну из функций :

• несамодвойственную

• несохраняющую 0

• несохраняющую 1

• немонотонную

• нелинейную

Доказательство :

Доказательство теоремы сводится к доказательству утверждения : имеет несамодвойственную, несохраняющую 0 и 1 функции можно получить конст-ты 0 или 1. Если тезис будет доказан, то теорема сводится к первой теореме о функциональной полноте.

Начнем доказательство с того, что покажем как с помощью несамодвойственной функции получить конст-ту, если имеется конст-та х и . Допустим, что имеется несамодвойственная функция f отn аргументов, тогда для нее можно найти такой набор , чтобы выполнялось равенство :

f (₁, ₂, …, _n) = (₁, ₂, …, _n)

Определим функцию f ( x )

f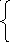( x ) = f ( x^1, x^2, …, x^n), где

x, _i = 1

x^i =

, _i = 0, при этом

0^i = _i , 1^i =_i , тогда

f ( 0 ) = f ( 0^1, 0^2, …, 0^n) = f ( ₁,…, _n) = f (₁, …, _n) = f ( 1^1, …, 1^n) = f ( 1 )

т.е. f ( x ) = const.

Рассмотрим 2 случая для функции несохраняющей 0 :

1. Имеем функцию несохраняющую 0 следующего вида :

f₀ ( x₁, …, x_n )

d₀ ( 0 ) = f₀ ( 0, …, 0 ) = 1

d₀ ( 1 ) = f₀ ( 1, …, 1 ) = 0  d₀ ( x ) =

А если есть х и , то подставив их в несамодвойственную функцию получим коснтанту, если понадобится противоположная конст-та, то ее можно получить отрицанием.

2. Имеем функцию несохраняющую 0 вида :

f₀ ( x₁, …, x_n )

d₀ ( 0 ) = f₀ ( 0, …, 0 ) = 1

d₀ ( 1 ) = f₀ ( 1, …, 1 ) = 1  d₀ ( x ) = 1

Имеем конст-ту 1.

Для получения конст-ты 0 используем функцию несохраняющую 1 вида :

f₁ ( x₁, …, x_n )

d₁ ( 1 ) = f₁ ( 1, …, 1 ) =   d₁ ( d₀ ( x )) = 

т.е. получена конст-та 0.

Таким образом доказана достаточность теоремы.

Доказательство необходимости теоремы следует из замкнутости классов самодвойственных, сохраняющих 0 и 1 функций.

Таким образом теорема доказана.

На основании 2^-й теоремы о функциональной полноте, построим расширенную таблицу Поста:

yi	Kн	Кл	K0	K1	Kc
f1		1			1	a
f2	1	1		1	1	b
f6	1			1	1	c
f7		1			1	d
f8	1	1	1	1	1	e
f9	1		1		1	f
F12	1		1	1		g
F13	1	1	1		1	h
F14	1	1	1	1	1	k

х1	х2	F1	F2	F6	F7	F8	F9	F12	F13	F14
0	0	0	0	0	0	1	1	1	1	1
0	1	0	0	1	1	0	0	1	1	1
1	0	0	1	1	1	0	0	0	0	1
1	1	1	0	0	1	0	1	0	1	0

F1 = х1*х2

F2 = х1*2 = х1х2  x1

F6 = 1*х2 + х1*2 = х1х2

F7 = х1 + х2 = х1х2  x1  х2

F8 = 1*2 = х1х2  x1  х2  1

F9 = 12 + х1х2 = х1х2  1

F12 = 1 = х1  1

F13 = 1 + х2 = х1х2  x1  1

F14 = 1 + 2 = х1х2  1

1 - не принадлежит классу.

С помощью метода Квайна найдем мин. покрытие табл., т. е. Получим все базисы в узком смысле в пр-ве Р_

P = ( b + c + e + f + g + h + k )( a + b + d + e + h + k )( e + f + g + h + k ) &

& ( b + c + g + k )( a + b + c + d + e + f + h + k ) = e + k + ( b + c + f + g + h )

( a + b + d + h )( f + g + h )( b + c + g )( a + b + c + d + f + h ) =

= e + k ( h + b + ( c + f + g )( a + d ) (a + c + d + f))( f + g + h )( b + c + g ) =

= e + k + (h + ac + b + a + af + ag + dc + df + dg )( g + bf + bh +c + ch) =

= e + k + hg + hb + hc + bg + bf + acf + ag + dcf + dg.

П₁= {f₈} П₆= { f₂ ,f₁₂}

П₂= {f₁₄} П₇= { f₂ ,f₉}

П₃= {f₁₂ ,f₁₃} П₈= { f₁ ,f₆,f₉}

П₄= { f₂ ,f₁₃} П₉= { f₁ ,f₁₂}

П₅= { f₆ ,f₁₃} П₁₀= { f₆ ,f₇,f₉}

П₁₁= {f₇,f₁₂}

Если результаты исследования базисов в узком смысле объед., то можно сделать вывод, что общее число всех возможных различных базисов равно 17.

Если сравнить базисы в узком смысле с базисами в широком смысле, то можно выявить следующие соответствия :

П₁В₂

П₂В₄

П₉В₁₀

П₁₁В₉

На основани базисов в узком смысле можно реализовать любую Булеву функцию.

Приведем Р⁵, его сост-т следующие функции :

{y₂, y₉}= П₇

y₂(x₁, x₂) = x₁₂

y₉(x₁, x₂) = x₁  x₂

_{x1 x1}

_x2 ^{& f 2} _x2 ^{f 9}

Через имеющиеся функции выразим функцию отрицания, для этого с помощью у₉ получим константу 1.

y₉(x , x ) = 1, тогда y₂( у₉ (x , x ) =

Используя функцию отрицания и y₂ получим конъюкцию :

y₂( x₁ , y₂ (у₉ (x₂ , x₂), x₂ )) = x₁x₂

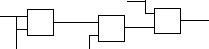_x1

_x2

_{& x2} ^& _x1x2

Имея функцию отрицания и конъюкцию, можно реализовать произвольную булеву функцию.

Если рассматривать базисы в узком и широком смысле с практической точки зрения, то следует отметить, что базисы в узком смысле не имеют никаких преимуществ, так как на практике всегда имеются константы 0 и 1.

СИНТЕЗ КОМБИНАТОРНЫХ СИСТЕМ.

Комбинаторной системой называется автомат выполняющий преобразование х в у, где

x={ x₁, x₂, …, x_n } – множество входных булевых переменных

y={ y₁, y₂, …, y_n } – множество выходных булевых функций

Отличительной особенностью комбинаторных систем является то, что выходной сигнал в момент времени T является функцией только входного сигнала в момент времени Т. В общем виде на стр-ных и функциональных схемах комбинаторные системы изображаются в виде перевернутой трапеции.

x₁ x_n

КС

у₁у_n

КС представляет собой схемы, состоящие из логических элементов. Каждый логический элемент реализует элементарную булеву функцию. Минимальная совокупность логических элементов достаточное для реализации произв-ной системы называется эл-ным базисом.

Алгоритм синтеза логических функций с малым числом переменных в заданном базисе :

1. Функция записывается в сов. норм. дизъюнктивной форме по заданной таблице истинности

2. Находится мин. форма, любым способом.

3. Операции дизъюнкции, конъюкции и отрицания варажаются через функции базиса.

4. Записывается выражение функции в элементах базиса и строится схема.

Пример.

Функция задана таблицой истинности :

x1	x2	x3	f
0	0	0	1
0	0	1	0
0	1	0	1
0	1	1	1
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	1

Минимизируем графическим методом :

111 110

_{011 010}

f ( x₁, x₂, x₃ ) = x₂x₃ + ₁x₂ + ₂₃

_{101 100}

001 000

Реализуем функцию в базисе В₆={ у₆, у₇ }

у₆(x₁, x₂) = x₁  x₂

y₇(x₁, x₂) = x₁ x₂

^{x1 x1}

^x2 _у6 ^{x2 1} _у9

Выразим в заданном базисе функцию отрицания у₆(x, 1) =

Выразим функцию конъюкции у₆ (y₇(y₆, 1), у₆(x₂, 1),1) = x₁x₂

Запишем выражение искомой функции

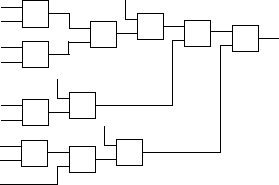
f ( x₁, x₂, x₃ ) = y₇ [у₆ (y₇(y₆(x₂, 1), y₆(x₃, 1)),1),y₆(y₇(x₂,x₃),1), y₆(y₇(x₁, y₆(x₂,1)),1)];

Построим схему данной функции :

_{1 1}

_{x2 1 1}

^{1 1} _{f ( x1, x2, x3 )}

_{x3 1}

¹

₁

_x2 ¹

^x3 ₁

¹

_x2 ^{1 1}

x3

Если число аргументов функций велико, то описанный способ синтеза комбинаторных схем становится громоздким и трудоемким.

Для синтеза схем с большим числом переменных существуют более эффективные методы. Один из них :

МЕТОД КАСКАДОВ.

Основанием для метода является теор. Шиннона, исходя из которой произв. Функция может быть представлена в следующем виде :

f(x₁, … , x_n) = _i f(x₁, …, x_i-1,,x_i+1, …, x_n)+f (x₁, …,x_i-1,1,x_i+1,…, x_n ) =

= _i f (  ) + x_i f( 1 )

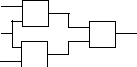
Эту функцию можно реализовать следующей схемой :

_f1

^&

_xi

_{1 f}

_&

^f0

Это устройство – каскадный элемент, который на схемах обозначают в следующем виде :

_{f1 &}

₁

_{x1 & f}

_f0

С помощью данного каскада получено представление от n аргументов, через остат-ные функции f₀и f₁для функций от n-1 аргумент, с помощью искл. х_iперемен.

На втором шаге каскада реализуется искл. следующая перемен. И далее поступая также мы получим остат – ные функции.

Это – каскадный метод – при этом каждый каскад соответствует исключению некоторой переменной. Для одной и той же функции можно получить несколько реализаций. Число реализаций равно :

N ( N - 1)( N – 2) - … = n!

Отсюда следует, что найти самую эффективную реализацию простым перебором весьма затруднительно.

Поэтому для метода должна быть найдена эффективная стратегия. Это позволяет сделать аппарат произв – ных от булевых функций. Пр – ная от функции n-аргументов.

=f (x₁,…, x_i-1,,x_i+1,…, x_n)f (x₁, …, x_i-1,1,x_i+1, …, x_n)

Пример :

Найти пр-ную от функции двух переменных

f (x₁,x₂) = x₁+ x₂

= x₂ (1 + x₂) =₂

Повторные пр-ные определяются следующим образом :

=() и т. д.

Пр-ная от булевой функции определяет условия при которых функция зависит от х_i

f (x₁,…, x_i-1,,x_i+1,…, x_n)f (x₁, …, x_i-1,1,x_i+1, …, x_n) т.е. при изменении х_iменяется значение функции. ( функция зависит от перем.)

Если пр-ная равна 0, то функция от х_iне зависит, т.е. при изменении х_iзначение функции не меняется.

Рассмотрим пример:

f (x₁, x₂, x₃, x₄) = x₁x₂x₃ +₁х₄+ x₂x₃ + x₁₃x₄

Определить при каких условиях функция зависит от переменной х₃. Найдем соответствующую производную :

= (₁х₄ +х₁х₄)(х₁х₂+₁х₄+х₂) = х₄( х₂+₁х₄) =

= х₄₂₁х₄+₄( х₂+₁х₄) = х₄₂(х₁+₄) +₄х₂ =₄х₂+ х₄₂х₁

Ответом на поставленную задачу будут значения х₁, х₂ , х₄при которых

= 1.

Составим соответствующую таблицу:

х1	х2	х4
0	0	0	0
0	0	1	0
0	1	0	1
0	1	1	0
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	0

х1	х2	х4
0	1	0	1
1	0	1	1
1	1	0	1

На этих наборах функция зависит от переменной х₃.

Первый шаг каскадной реализации.

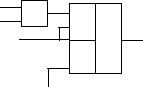
_{х1 & & 1}

^х4

_&

_f0

f₀ ( x₁,x₃,x₄) =₁+₃₄+ x₃x₄=₁+

Введем определение :

Весом пр-ной функции называется количество возможных наборов, при которых производная равна 1. Исходя из предыдущего примера сложность производной по х₃() равна 3.

Запишем утверждение :

Чем больше состояний имеет функция, прикоторых она зависит от x_i, тем сильнее она зависит от этой переменной.

Для примера выясним от какой переменной функция зависит сильнее.

f ( x₁, x₂, x₃,x₄) = x₁x₂x₃+₁x₄+ x₂x₃+ x₁₃x₄

W ( ) = 3

= ( x₄+x₂x₃ )(x₂x₃ +₃x₄)

х1	х2	х4
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	0
1	1	1	0

W () = 1

= (₁x₄+ x₁₃x₄)( x₁x₃+₁x₄+ x₃+ x₁₃x₄) =(x₄₁+ x₄₃)( x₃+ x₄)

х1	х2	х4
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	0
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

W ( ) = 3

=(x₁x₂x₃+ x₂x₃)(x₁x₂x₃+₁+ x₂x₃+ x₁₃) = x₂x₃(x₂+₁ +₃ )

х1	х2	х4
0	0	0	1
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	1
1	1	1	0

W ( ) = 5

Оказалось, что сильнее всего функция зависит от переменной х₄. При этом видно, что чем сильнее зав-ть функции, тем меньше сложность ост-ной функции при ее искл-нии.

Для функции заданной таблично удобно использовать следующий метод определения веса производной:

Рассмотрим на примере :

Функция от четырех переменных задана таблицей истинности :

х1	х2	x3	x4	f
0	0	0	0	0
0	0	0	1	1
0	0	1	0	1
0	0	1	1	1
0	1	0	0	0
0	1	0	1	1
0	1	1	0	0
0	1	1	1	1
1	0	0	0	1
1	0	0	1	0
1	0	1	0	1
1	0	1	1	0
1	1	0	0	1
1	1	0	1	1
1	1	1	0	0
1	1	1	1	0

Для заданной функции определить веса производных по х₁,х₂, х₃, х₄.

x2	x3	x4	1	0	d
0	0	0	1	0	1
0	0	1	1	1	1
0	1	0	1	1	0
0	1	1	0	1	1
1	0	0	1	0	1
1	0	1	1	1	0
1	1	0	0	0	0
1	1	1	0	1	1

Cтолбцы 1 и 0 заполняются следующим образом :

Вместо искл. переменной в каждый набор подставляются значения 1 или 0 и выписывают соотв. стб. знач. Функции из исходной таблицы.

Столбец dполучается сложением поmod 2соотв. знач. стб. 1 и 0.

W₁ = 5

x₂ :

x1	x3	x4	1	0	d
0	0	0	0	0	0
0	0	1	1	1	0
0	1	0	0	1	1
0	1	1	1	1	0
1	0	0	1	1	0
1	0	1	1	0	1
1	1	0	0	1	1
1	1	1	0	0	0

W₂ = 3

x₃ :

x1	x2	x4	1	0	d
0	0	0	1	0	1
0	0	1	1	1	0
0	1	0	0	0	0
0	1	1	1	1	0
1	0	0	1	1	0
1	0	1	0	0	0
1	1	0	0	1	1
1	1	1	0	1	1

W₃ = 3

x₄ :

x1	x2	x3	1	0	d
0	0	0	1	0	1
0	0	1	1	1	0
0	1	0	1	0	1
0	1	1	1	0	1
1	0	0	0	1	1
1	0	1	0	1	1
1	1	0	1	1	0
1	1	1	0	0	0

W₄ = 5

Анализ производных показал, что для данного примера первыми исключ-ми переменными будут х₁и х₄.

Рассмотрим более сложную задачу для которой функция задана аналитически ( от 5^-ипеременных ).

f ( x₁, x₂, x₃, x₄, x₅ ) = x₁₂x₃ + ₁₃x₄ + x₁x₃₅ + x₁x₂x₄ + ₂x₃x₅ + ₃₄x₅

Для данного примера на картах Карно определим веса производных и первую искл. переменную. Затем на картах Карно определим вторую исключаемую переменную и т.д., а затем по полученным данным построим принц. Схему функции.

X₁X₂ x₃X₄X_{5 001 011 010 110 111 101 100}

00		1	1	1		1	1
01		1	1	1
11		1	1	1	1		1	1
10		1			1	1	1	1

W₁ = 7 ; W₂ = 5 ; W₃ = 9 ; W₄ = 5 ; W₅ = 7 ;

Первая искл. переменная х₃

Рассмотрим карту Карно для остальных функций: f ( 1 ) f ( 0 )

X₁X₂ X₄X_{5 00 01 11 10}

f (0) 00		1	1	1
01		1	1	1
11		1	1	1
10		1

W₁ = 2 ; W₂ = 2 ; W₄ = 4 ; W₅ = 4 ;

X₁X₂ X₄X_{5 00 01 11 10}

f (1) 00		1	1
01
11	1		1	1
10	1	1	1	1

W₁ = 5 ; W₂ = 3 ; W₄ = 1 ; W₅ = 3 ; Искл. х₁

Второй искл. переменной - х₄ или х₅.

Получим f (1,0) f (1,1).

x₂ x₄ x_{5 00 01 11 10}

0	1	1	1	1
1	1		1	1

f₁₁ = ₂ + ₅ + x₄ = + x₄

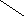x₂ x₄ x_{5 00 01 11 10}

0		1	1
1

f₁₀ = ₂ x₅

Функции f(0,0) и f(0,1) получ. искл. х₄.

f₀₀ = х₅ f₀₁ = ₁ + х₂

По имеющимся данным строим принц. схему каск. метода :

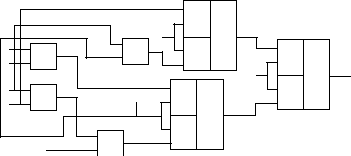^{f 00}

^{& 1}

₁ ^x4 _{f 0 & 1}

^& f 01

_{f 10 x3 f}

^{x4 & & 1} _{f 1} ^&

^{x5 x1}

^&

^{x4 &} _{f 11}

f₀₀ = х₅ f₀₁ = ₁ + х₂

АЛГЕБРА ВЫСКАЗЫВАНИЙ И ЛОГИКА ПРЕДИКАТОВ.

Логические связки алгебры высказываний:

НЕ - ИЛИ - Р q

И - & ЕСЛИ…, то - Рq(импликант)

Семантическая область алгебры высказываний содержит всего 2 значения:

истина и ложь( 1 и 0 ). Каждое элементарное высказывание обозначается малыми латинскими буквами (литералы). Используя элементарные высказывания и логические связки, можно составить сложные высказывания. Алгебра высказываний базируется на алгебре Буля, а в алгебре Буля аналогично высказываниям – функция.

Если некоторое высказывание в качестве аргументов имеет mлитералов, то оноm– местное.

Буквой Е в высказываниях обозначается множество всех высказываний от m– аргументов. Все множество высказываний можно разделить на 3 класса:

1. Общезначимые высказывания (тарфтология)

2. Выполнимые высказывания.

3. Невыполнимые высказывания.

Общезначимое - высказывание , принимающее значение ИСТИНА для любых наборов литералов.

Выполнимые – высказывания, которые имеют хотя бы одну интерпретацию.

Интерпретационные высказывания – некоторый набор литералов, при котором высказывание принимает значение ИСТИНА.

Высказывание, которое не имеет на одной интерпритации, называется невыполнимым.

Основными задачами алгебры высказываний являются алгоритмы определения выполнимости и общезначимости высказываний. Так как АВ базируется на Булевой алгебре, то все методы последней применимы к первой , в том числе и методы представления функций.

Основная форма представления высказываний является ДСНФ ,а иногда и КСНФ.

p	q	v	y
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	1
1	1	1	0

ДСНФ

f( p, q, v ) =vqppq

КСНФ

f ( p, q, v ) = ( p qv ) & ( p)(q) & ()

ДСНФ и КСНФ можно свести к ДНФ и КНФ.

Сведем КСНФ к КНФ.

p _{q v 00 01 11 10}

0	0		0
1		0	0

КНФ

f ( p, q, v ) = ( p qv ) & () & ()

Анализ высказываний, представленных в ДНФ.

Задача в ДНФ общезначна, если каждый из ее элементов общезначен (дизъюнкт). Высказывание выполнимое в ДНФ , если выполним хотя бы один дизъюнкт.

Пример.

Дано сложное высказывание, зависящее от 3-х литералов p, q, r, заданное таблично:

p	q	r	A1	A2
0	0	0	1	0
0	0	1	1	0
0	1	0	0	1
0	1	1	1	1
1	0	0	1	0
1	0	1	0	1
1	1	0	1	1
1	1	1	1	1

Представим высказывания А₁и А₂в ДНФ, для этого составим карты Карно :

А₁ p _{q r 00 01 11 10}

0	1	1	1
1	1		1	1

A₁ = qr + + p

А₂ p _{q r 00 01 11 10}

0			1	1
1		1	1	1

A₁ = q + pr

Тогда высказывание f имеет вид:

f = qr + + p+ q + pr

По полученному fможно сделать вывод, что высказывание является выполнимым. Это следует из того ,что выполнимым является 1 из дизъюнктов, например pr , еслиp = 1 иr = 1 , то pr = 1и следовательно все высказывания принимают значениеtrue.

Логика высказываний занимаетсяся логическими связями, а логика предикатов проникает в структуру высказываний и исследует связь того, о ком или о чем идет речь (субъект) с тем, что говорится о данном объекте (предикат). Поэтому язык логики предикатов лучше приспособлен для выражения логических связей между различными понятиями и утверждениями P(x₁, x₂, …,x_n).

N – местный предикат есть неоднородная двузначная логическая функция

Аргументы х₁,х₂,х_nпредставляют собой объекты из множеств их представления, т.е. х₁х₁

х₂х₂

Конкретное значение аргументов называют предметными постоянными. Предметные переменные и constобразуют класс логических понятий – термы. При замещении аргумента Х_к(предметvar), некоторым его значениям а (предмет const)n – местный предикат р(х₁,х₂, …,х_n) превращается в( n – 1 ) местный предикатp(x₁,x₂,…k_i-1,a,k_i+1,x_n).И от переменной х_n он уже не зависит. Присвоив значение всем переменнымn местного предиката из соответствующих областей определения, мы получим высказывание,которое можно рассматривать как О местный предикат.

Например: дан 3-х местный предикат p(x₁,x₂,x₃) для которых х₁есть сумма х₂и х₃

При подстановке х₁= 5 он переходит в двуместный предикат вида

р (5,х₂,х₃)

При подстановке х₂= 2 он переходит в одноместный предикат вида

р (5,2,х₃)

При х₃= 3 , он становится истинным высказыванием

При х₃3 - ложным.

В логике предикатов большое значение имеют две операции, которые называются КВАНТОРН., с помощью которых выражается отношение общности к существованию.

Пусть предикат р(х) определенный на множестве М , утверждение , что все х М и обладают свойством р(х) , записывают с помощью квантора общности

 x p(x) {Для всех х,р(х) }.

Утверждение ,что существует хотя бы 1 объект х из множества М , обладающий свойством р(х), записывается с помощью квантора существования:

 х р(х) {существует такой х, что р(х)}

В этих двух выражениях встречаются переменные х , но они не зависят от значения этой переменной. Кванторы общности и существования связывают переменные х , превращая одноместный предикат в высказывание.

Рассмотрим предикат р(х) , где х – простое число. Предикат р определен на множестве натуральных чисел. Подставляя вместо х числа натурального ряда, получаем счетное множество высказываний. Некоторые из них р(1),р(2),р(3)…. являются истинными. Высказывание  х р(х) – ложное, ах р(х) для 2-го предиката (некоторые числа простые) – истинными.Между кванторами общности и существования имеют место соотношениния, обобщающие законы де Моргана вида:

х р(х) =х

х р(х) = х

Применение квантора к n– местному предикату, превращает его в (n – 1)местный предикат. Кванторы можно также применять к нескольким различным переменным ( по 1 квантору к-л. типа к каждой переменной). Если кnместному предикату применяетсяk кванторов, то он превращается в

(n – k)предикат.

Переменные , к которым применяются кванторы – связанные , остальные переменные – свободные.

Например: из двуместного предиката р(х,у) можно получить следующий одноместные предикаты:

 x p(x,y)

 x p(x,y)

 y p(x,y)

 y p(x,y)

а так же высказывания:

 x  y p(x,y);

 x  y p(x,y);

…………………

 x  y p(x,y); и т.д.

Порядок следования одноименных кванторов не имеет значения, но разноименные переставлять нельзя.

 x y p(x,y)   y  x p(x,y)

x  y p(x,y)   y  x p(x,y)

В этом можно убедиться на примере:

p(х,у) = << x делит у >>

 x  y << xделит у >> - это высказывание истинное

 y  x << y делитx>> - это высказывание ложное.

Категорические высказывания.

В традиционной логике большое внимание уделяется 4-м типам категорических высказываний , которые обозначаются: A, E, I, O.

А – общеутвержденное высказывание.

<< Всякое S суть P >>

Для всех х ,если х обладает свойством S , то х обладает и свойством р.

 x ( S(x)  p(x))

Е – общеотрицательное высказывание

<< никакое S не естьp >>

 x ( S(x)  )

Для всех х , если х обладает свойством S ,то он обладает свойством р.

I - частноутвердительное высказывание.

<< некоторое S суть р>>

 x ( S(x) & p(x))

cуществует такой объект х , который обладает свойствомS и одновременно обладающий свойством р.

О – частноотрицательное высказывание

<< некотороеSне суть р >>

 x ( S(x) & )

существует такой объект х, который обладает свойством S и не обладает свойством р.

Пример: S(x) = << x – селедка>>

p(x) = << x – рыба>>

Четырем типам высказываний соответствуют утверждения:

А : всякая селедка – рыба

Е : никакая селедка не является рыбой

I: некоторая селедка – рыба

О : некоторая селедка не является рыбой

В законах де Моргана эти категоричные высказывания выглядят следующим образом:

 x (S(x)  p(x))  x (S(x) &);

 x (S(x)  ) x (S(x) & p(x));

x (S(x)  )  x (S(x) & p(x));

x (S(x)  p(x))   x (S(x) & );

Высказываеие А и О, а так же Е и Iотличаются друг от друга. Если одно из них истинное, то другое – ложно и нызываются противоположными.

ЭЛЕМЕНТЫ ТЕОРИИ АВТОМАТОВ.

Конечный автомат:

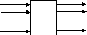^{x1 y1}

_{……… КА ………}

^{xn yn}

Рассмотрим следующий элемент:

Дано некоторое логическое устройство ,имеющее один вход и один выход:

_{х1 у1}

На вход подается некоторая двоичная последовательность: х = 011101001101

Алгоритм устройства следующий:

Выходом У будет текущего и предыдущего элемента вход. последовательности:

У = 10011101011

С помощью логических устройств, которые мы рассматривали ранее, данная задача не выполнима. Для решения этой задачи нужно применить устройство конечного автомата.

Основные определения:

Декарт. Произведение 2-х множеств АВ называется множество С ,элементы которого составляют пары исходных элементов 2-х множеств.

Пример: С = А*В; А{a₁,a₂,a₃}; B{b₁,b₂}

C{(a₁,b₁),(a₁,b₂),(a₂,b₁),(a₂,b₂),(a₃,b₁),(a₃,b₂)}

Конечный автомат – объект определенный 5-ю параметрами:

1) S = < A, Q, V, ,  >

A – множество букв входящего алфавита;

Q – множество сост. автомата;

V – множество букв выход. алфавита;

 : A*Q  Q - функция переход. КА;

 : A*Q  V - функция выходов

Пример конечного автомата: Задан вход и выход , набор , и набор состояний:

A = {a₀,a₁}, V = { V₀, V₁}, Q = { q₀, q₁, q₂}.

Одним из способов задания функции переходов и выходов является табличный метод:

Функция переходов Функция выходов

	q0	q1	q2				q0	q1	q2
a0	q1	q0	q2			a0	v0	v1	v1
a1	q2	q1	q0			a1	v1	v1	v0

С помощью 2-х функций из 3-х исходных множеств полностью задается КА.

Кроме табличного способа задания КА можно использовать аппарат графов.

Граф – топологический объект , основными элементами которого являются вершины.

1 2 1,2 – вершины

Ребро графа может соединять вершины и входить само в себя.

1. Неориентировочные графы.

1 2

Для данного графа имеет значение соединение между собой, направления не учитываются.

2. Ориентировочные графы.

1 2

Для них важно, какие вершины соединяются и направление соединения.

Словом  называется некоторая последовательность букв входного алфавита.

 = а_j1, a_j2, …, a_jn;

при этом для функции перехода и выходов справедливы соотношения:

 (q, a) =  (  (q,  ),a);

 (q, a ) =  (  (q,  ),a);

Допустим, что автомат находится в состоянии q_i и на его вход поступает последовательность букв:=a_j1, a_j2, …, a_jn, тогда на выходе автомата будет наблюдаться w следующего вида:

w =  (q_i, a_j1)  (q_i, a_j1, a_j2) …  (q_i, a_j1, a_j2, a_j3, …, a_jn)

Другими словами автомат находится в состоянии q_i, переводит входное слово

 в выходное w. Другими словами это записывается в виде:

S (q_i, ) = w;

где функция S – автоматный оператор.

ЭКВИВАЛЕНТНЫЕ СОСТОЯНИЯ И АВТОМАТЫ.

Два состояния q_iиq_jназываются эквивалентными, если выполняется равенство:S (q_i, ) = S (q_j, )для произвольного.

В простейшем случае , когда входящее слово состоит из одной буквы, эквивалентность имеет вид: (q_i,a) =  (q_j,a)

Множестваво всех эквивалентных состояниях называются классом эквивалентности К.

Допустим q_i и q_jпринадлежит классу К₀,сформируем словоследующим образом= а₀а₁,тогда согласно определению эквивалентности мы можем записать.

S ( q_i, а₀, а₁) = S ( q_j, а₀, а₁)

Полученное равенство запишем в ином виде :

 ( q_i, а₀ ) ( q_i, а₀, а₁) =  ( q_j, а₀ ) ( q_j, а₀, а₁)

Исходя из определения эквивалентности : выполняется равенство:

 ( q_i, а₀ )=  ( q_j, а₀ ),

а значит выполняется и равенство:

 ( q_i, а₀, а₁) =  ( q_j, а₀, a₁ )

Преобразовав получим равенство :

 (  ( q_i, а₀), а₁) =  (  ( q_j, а₀), а₁)

Для того, чтобы две составляющиеq_i иq_j были эквивалентны, должны выполнятся следующие условия :

 ( q_i, а ) = ( q_j, а )

 ( q_i, а ) = ( q_j, а ) K

Используя свойства эквивалентных состояний, множество сост. заданного автомата всегда может быть разбито на соответствующие классы эквивалентности.

Рассмотрим следующий пример :

Автомат задан графом вида :

А = {0, 1}; V = {0, 1}

Q = { q₁, q₂, q₃, q₄, q₅, q₆, q₇ }

q₂ q₆

q₁ q₄ q₇

q₃ q₅

Составим таблицы выходов и функции перехода :

	q1	q2	q3	q4	q5	q6	q7
0	1	1	0	0	1	0	0
1	0	0	1	1	0	1	1

	q1	q2	q3	q4	q5	q6	q7
0	q2	q5	q7	q1	q5	q4	q5
1	q3	q6	q4	q3	q6	q7	q6

Используя два условия эквивалентности разобьем множество сост. автоматов на классы эквивалентности :

1. Получение класса условно эквивалентных сост. ( проверяем условие выполнения первого равенства ). Используя таблицу выходов мы можем записать два условно эквивалентных класса.

к₀={q₁ q₂ q₅}

к₁={q₃ q₄ q₆ q₇}

2. Проверка эквивалентности полученных классов:

	q1	q2	q3	q4	q5	q6	q7
0	к0	к0	к1	к0	к0	к1	к0
1	к1	к1	к1	к1	к1	к1	к1

На основании полученной таблицы и второго условия эквивалентности

делаем вывод : класс к₁ распадается на два класса :

к₁^,={q₃ q₆} к₁^”={q₄ q₇}

3. С учетом нового разбиения на классы опять заполняется таблмца перехода :

	q1	q2	q3	q4	q5	q6	q7
0	к0	к0	к1”	к0	к0	к1”	к0
1	к1’	к1’	к0	к1’	к1’	к1”	к1’

В результате решения задачи получены три класса эквивалентности :

к₀ = { q₁, q₂, q₅}

к₁^’ = { q₃ q₆}

к₁^” = { q₄ q₇}

Для проверки подадим на вход последовательность :

	q1	q2	q6	q7	q6	q4	q3	q4	q1	q2
	0	1	1	1	0	1	1	0	0	1
	1	0	1	1	0	1	1	0	1	0

	q5	q3	q6	q7	q6	q4	q3	q4	q1	q2
	0	1	1	1	0	1	1	0	0	1
	1	0	1	1	0	1	1	0	1	0

Автоматы S и Т называются эквивалентными, если любому сост. автоматаS найдется сост. автомата Т. ( и наоборот)

Если автомат S₀ эквивалентен автоматуS и количество сост.S₀ > S, тоS₀ – минимальный автомат ( единственный ).

Построим мин. автомат S₀ для нашего примера:

q₀₁  k₀ q₀₂  k₁’ q₀₃  k₁^”

q₀₂

q₀₁

q₀₃

0	q01	q02	q03
0	1	0	0
1	0	1	1

	q01	q02	q03
0	q01	q03	q01
1	q02	q03	q02

РЕАЛИЗАЦИЯ КА.

КА состоит из двух остальных блоков:

1. реализует функцию переходов;

2. реализует функцию выходов.



_{qi  (qi, aj)}

^aj

_qi

_{aj aj} ^{ (qi, aj)} v_k

В этой схеме используют устройство, реализующее задержку перехода автомата в новое состояние на время .

Если  одинаково для любых состояний, то автомат синхронный, иначе асинхронный.

Блок функций выходов и переходовмогут быть реализованы комбинаторными системами.