Соединения без повторений

Соединения – простые комбинаторные объекты, к которым относят перестановки, сочетания и размещения.

Перестановки

Перестановка изnэлементов – упорядоченная последовательность элементовn- элементного множества (кортеж).

Различные перестановки отличаются толькопорядком элементов в них.

Определим 0!=1

Числоперестановок из n различных элементов равно:

Например:

Пусть A = {1,2,3}.Число различных перестановок равно 3!=6.

Перестановки: {123, 132, 213, 231, 312, 321}.

Например:

1. Число способов стать в очередь за стипендией из 17 человек?

P₁₇=17!

2. Сколькими способами можно расставить на полке 5 книг?

P₅=5!

3. Сколько различных слов можно образовать, переставляя буквы в слове "ковш"?

P₄=4!

Размещения из n элементов по m без повторений

Размещения – упорядоченная последовательность изmэлементов множества, содержащего всегоnэлементов.

Различныеразмещения отличаются составом элементов и (или) порядком их следования.

Например:

Пусть A={1,2,3}.

Размещения из 3 по 2: {12, 21, 13, 31, 23, 32}.

Н

Числоразмещений из n различных элементов по m равно

апример:

1. Сколькими способами можно расставить на полке 5 книг из 7?

2. Сколько различных четырёх-символьных идентификаторов можно получить в алфавите {A,B,C,D,E}.

Замечание: Формула верна для всех m  n.

При m = n .

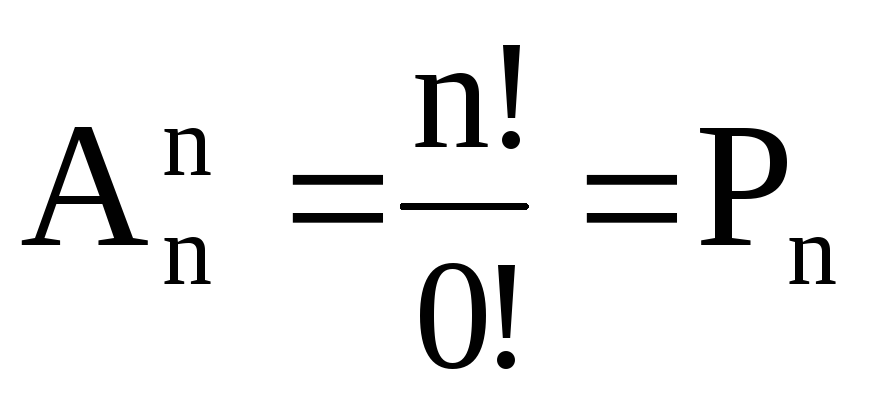Сочетания без повторений

Сочетания изnпоm – набор изmэлементов n-элементного масива, без учета порядка элементов в наборе.

Сочетание – произвольное (неупорядоченное)m-подмножество изnэлементов.

Р

Число сочетаний из n различных элементов по m равно:

, m ≤ n.

азличныесочетания отличаются составом элементов, но не их порядком.

Свойства числа сочетаний

1)  ;

;; ; при m  0 и m n .

2) Симметричность числа сочетаний:.

3) Правило Паскаля:

Для числа сочетаний из n по m справедливо следующее рекурентное cоотношение: .

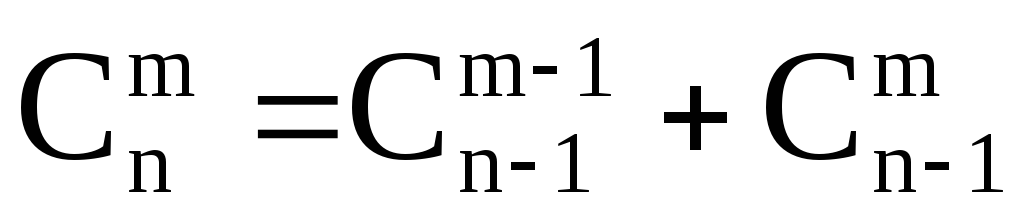4) Бином Ньютона:

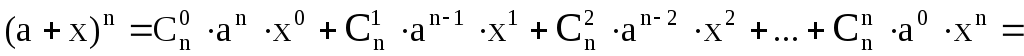
При a = x = 1, ,

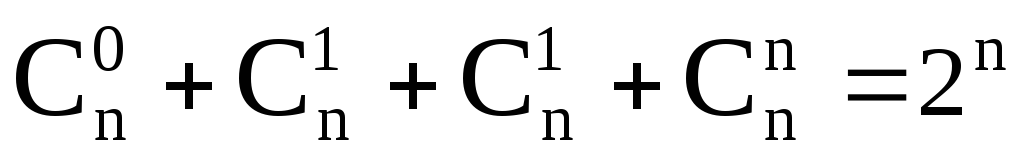
, k = 0,1… n - биноминальные коэффициенты .

Например:

A={1,2,3}

Сочетания из 3 по 2 : {12, 31, 32}.

Соединения с повторениями

До сих пор рассматривали соединения из множеств, состоящих из различных элементов. Часто на практике имеют место случаи, когда среди рассматриваемых элементов есть одинаковые.

Пусть дано множество А, состоящее из n элементов, в котором n₁ элементов принадлежит первому типу; n₂ элементов принадлежит второму типу элементов, n_k - k-тому типу. Элементы одного и того же типа неразличимы между собой.

Спецификацией множества А называется набор (n₁, n₂, … ,n_k).

С

Число перестановок с повторениями n - элементного множества с

заданной спецификацией равно

, где .

ледствие:

Если множество А, | А | = n, состоит из объектов 2 типов: m-одного типа, (n – m) –другого:

.

В общем случае:

.

Например:

Сколько различных чисел можно получить, переставляя цифры числа 12341234?

Решение:

В числе 8- чифр: две-“1”; две-“2”; две-“3”; две-“4”. .

Например:

Сколько различных перестановок можно образовать из всех букв слова “Миссисипи”?

Решение:

Всего в слове 9 букв, из них – 4 буквы “и”, три буквы ”с”, одна буква ”м” и одна буква ”п”.