Отношение эквивалентности

Бинарное отношение, обладающее свойствами рефлексивность, симметричность, транзитивность называется отношением эквивалентности (обозначается  ).

= { (x, y) | x=y, x,y  N },

= { (x, y) | x=y(mod m), x,y  N }.

На множестве людей: “иметь одно имя”, ”обучаться в одной студенческой группе ”.

На множестве множеств: “A=B”.

Разбиения и покрытия множества

Покрытием непустого множества называется совокупность подмножествтаких, что:

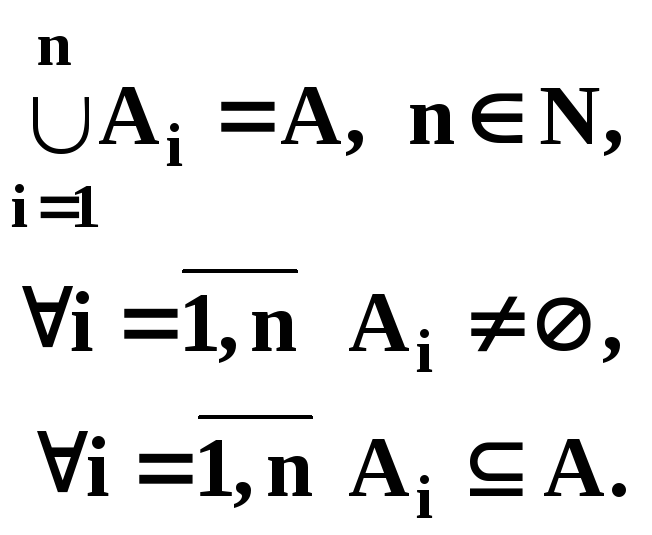
Разбиением непустого множества называется совокупность подмножествтаких, что:

Класс эквивалентности для х: [ x ] = { y Х | x  y }.

Например:

Отношения  и  заданы на множестве Х = {1, 2, 3, 4, 5, 6,}.

 = {(1,4), (2,5), (3,6), (4,1), (6,3)},

 = {(1,1), (2,3), (3,4), (4,5), (5,6), (6,6)}.

Область определения D_ = {1, 2, 3, 4, 6}.

Область значений J _ = {1, 3, 4, 5, 6}.

Обратное отношение ^-1 = {(4,1), (5,2), (6,3), (1,4), (3,6)}.

Отношение  - антирефлексивно, не симметрично, не транзитивно.

Область определения D_ = {1, 2, 3, 4, 5, 6}.

Область значений J _ = {1, 3, 4, 5, 6}.

Отношение  - не рефлексивно, антисимметрично, не транзитивно.

Композиция  ○  = {(1,5), (2,6), (3,6), (4,1), (6,4)}.

Например:

Отношение = {(x, y) | сравнение по модулю m, x,y  N}.

Отношение сравнения по модулю m на множестве натуральных чисел: x = y mod m, что означает: “x и y имеют одинаковый остаток при делении на m (классы вычетов по модулю m)”.

Отрезок натурального ряда N₄={1,2,3,4}

Отношение сравнения по модулю 2 на N₄:

 = { (1,1),(1,3),(2,2),(2,4),(3,1),(3,3),(4,2) ,(4,4)}.

Область определения D_ = {1, 2, 3, 4}.

Область значений J _ = {1, 2, 3, 4}.

Отношение  - рефлексивно, симметрично, транзитивно.

Отношение  - отношение эквивалентности.

Классы эквивалентности: [ 1 ]={ 1,3 }=[ 3 ]

[ 2 ]={ 2,4 }=[ 4 ].

Например:

Отношения  и  заданы на множестве N_{4 .}

 ={ (1,2), (2,3), (1,3), (3,4), (2,4), (1,4)}

={ (1,1),(2,2),(3,3),(4,4)}.

Область определения D_ = {1, 2, 3}.

Область значений J _ = {2, 3, 4}.

Отношение  - антирефлексивно, антисимметрично, транзитивно.

Отношение  - отношение строгого порядка.

Область определения D_ = {1, 2, 3 ,4}.

Область значений J _ = {1, 2, 3, 4}.

Отношение  - рефлексивно, симметрично, антисимметрично, транзитивно.

Отношение  - отношение нестрогого частичного порядка.

Отношение  - отношение эквивалентности.

Классы эквивалентности: [ 1 ]={ 1 }

[ 2 ]={ 2 }

[ 3 ]={ 3 }

[ 4 ]={ 4 }.

Функциональные отношения

Пусть   Х х Y.

Функциональное отношение – бинарное отношение :

 х  D_   y  Y: х  y .

Всюду определённое отношение – отношение, у которого D_ = Х ("нет одиноких х").

Сюръективное отношение – отношение, у которого J_ = Y ("нет одиноких y").

Инъективное отношение – отношение, в котором разным х соответствуют разные у.

Биекция – функциональное, всюду определённое, инъективное, сюръективное отношение, задаёт взаимно однозначное соответствие множеств.