Способы задания отношений

1) Список пар или характеристическое свойство.

Любое бинарное отношение (как множество) может быть задано в виде списка пар, из которых состоит отношение, или с использованием характеристического или определяющего свойства.

 = { (1,1), (2,2), (3,3), (4,4)} на   Х², Х = {1,2,3,4} или

}.

2) Матрица отношения.

В матрице отношения строки отвечают элементам множества , столбцы элементам множества, элемент матрицы равен:

Если , а, то матрица отношения имеет размерность

 ={(1,1), (2,2), (3,3), (4,4)} на   Х², Х = {1,2,3,4}.

	1	2	3	4
1	1	0	0	0
А= 2	0	1	0	0
3	0	0	1	0
4	0	0	0	1

3) Графическое изображение отношений.

На плоскости изображаются точками элементы множеств . Если парапринадлежит отношению, то соединяются точки, изображающие, линией, направленной от первого элемента ко второму. Обозначая таким образом все пары, принадлежащие отношению, получаем фигуру, которая называется графом отношения.

 ={(1,5), (2,4), (3,6), (6,2)} на   Х², Х = {1,2,3,4,5,6}.

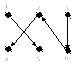
Операции над отношениями

Пусть -некоторое бинарное отношение.

Обратное отношение к отношениюопределяется следующим образом:

,

упорядоченная пара принадлежиттогда и только тогда, когдапринадлежит.

Если , то, если, то и

Композиция отношений  и  – бинарное отношение, состоящее из упорядоченных пардля которых существует элемент, такой, что выполняются условия,:= ○  = {(x, z)| х  у, y  z }.

Операция композиция отношений не коммутативна:, но ассоциативна

Свойства бинарных отношений

Пусть  задано на множестве X,   Х².

1. Рефлексивность:  х  Х х  х.

Отношение  на множестве X называется рефлексивным, если для любого хХ имеет место х  х, то есть каждый элемент находится в отношении  к самому себе.

Матрица рефлексивного отношения имеет единичную главную диагональ, а граф – петлю возле каждого своего элемента.

2. Антирефлексивность: х  Х х  х.

Отношение  на множестве X называется антирефлексивным, если не существует хХ такого, что имеет место х  х, то есть ни один элемент не находится в отношении  к самому себе.

Матрица антирефлексивного отношения имеет нулевую главную диагональ,а граф – не имеет ни одной петли.

3. Нерефлексивность:  х  Х (x, x)  .

4. Симметричность:  х, y  Х х  y => y  х.

Отношение  на множестве X называется cимметричным, если для всех х и y из Х, из принадлежности (x,y) отношению  следует, что и (y,x) принадлежит отношению .

Матрица симметричного отношения симметрична относительно главной диагонали, а граф – для каждой дуги (x,y) существует обратная дуга(y,x).

5. Антисимметричность:  х, y  Х х  y, y  х  x = y.

Отношение  на множестве X называется антиcимметричным, если для всех х и y из Х, из принадлежности (x,y) и (y,x) отношению  следует, что x=y.

Матрица антисимметричного отношения не имеет ни одной симметричной единицы относительно главной диагонали, а граф – длякаждой дуги (x,y) не существует обратная дуга(y,x) и наоборот.

Свойства симметричности и антисимметричности не являются взаимоисключающими, примером может служить отношения равенства на множестве натуральных чисел.

6. Транзитивность:  х, y, z  Х х  y, y  z => x  z.

Отношение  на множестве X называется транзитивным, если для всех х,y,z из Х, из принадлежности (x,y) и (y,z) отношению  следует, что (x,z) также принадлежит .

Отношение  на множестве X называется антитранзитивным, если для всех х,y,z из Х, из принадлежности (x,y) и (y,z) отношению  не следует, что (x,z) также принадлежит .

Отношение порядка – антисимметрично, транзитивно.

Отношение нестрого порядка () - рефлексивно, антисимметрично, транзитивно.

= { (x, y) | xy, x,y  N},

= { (x, y) | xy, x,y  N}.

На множестве множеств: “A  B”, “A=B”.

Отношение строгого порядка () - антирефлексивно, антисимметрично, транзитивно.

= { (x, y) | x>y, x,y  N},

= { (x, y) | x<y, x,y  N}.

На множестве множеств: “A  B”.

В отношениях полного порядка все элементы сравнимы между собой, а в отношениях частичного порядка не все элементы сравнимы между собой.

Отношения полного порядка:

= { (x, y) | xy, x,y  N },

= { (x, y) | xy, x,y  N }.

Отношения частичного порядка:

= { (x, y) | x>y, x,y  N },

= { (x, y) | x<y, x,y  N },

на множестве множеств: “A  B”, “A  B”.