Обходы графа

Эйлеров цикл – цикл, содержащий каждую дугу орграфа.

Эйлеров орграф – связный орграф, содержащий эйлеров цикл.

Например:

Критерий эйлеровости для орграфов

Для связного орграфа следующие условия эквивалентны:

1. Орграф G– эйлеров.

2. Для любой вершины справедливо: deg ⁺ (v)= deg ^- (v).

3. Орграф Gявляется объединением контуров, попарно не имеющих общих ребер.

Гамильтонов контур орграфа G – контур, содержащий все вершины данного орграфа.

Гамильтонов орграф G – орграф, содержащий гамильтонов контур.

База

База орграфа G –наименьшее (относительно включения) подмножество вершинB,удовлетворяющее условию:любаявершина v  V/B достижима из какой-либо вершиныu  B.

Базовая компонента – сильная компонента орграфа G, в которую не входит ни одна дуга из других сильных компонент.

В конденсации G^* таким компонентам соответствуют вершины с нулевыми полустепенями захода.

Подмножество вершин B орграфа G – база, если B состоит из вершин принадлежащих базовым компонентам, причем в каждую базовую компоненту входит ровно одна вершина из множества B.

Алгоритм нахождения базы

1. Построить конденсацию G^*.

2. Выделить в конденсации вершины с нулевыми полустепенями захода. Такие вершины будут определять базовые компоненты.

3. Из каждой базовой компоненты выбирается по одной вершине, таким образом, база орграфа может быть определена не единственным образом.

Антибаза

Антибаза орграфа G - наименьшее (относительно включения) подмножество вершинB, удовлетворяющее условию:любая вершинаvV, достижима из какой-либо вершиныvV/ B.

Алгоритм построения антибазы

1. Построить конденсацию G^*.

2. Выделить в конденсации вершины с нулевыми полустепенями исхода.

3. Из каждой компоненты, соответствующей такой вершине, выбирается по одной вершине.

Например:

Задан граф G. Найтибазу иантибазу.

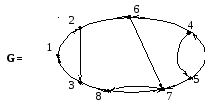
Решение:

Построим конденсацию G^*:

Матрица достижимости R_G :

	1	2	3	4	5	6	7	8
1	1	1	1	0	0	1	1	1
2	1	1	1	0	0	1	1	1
3	1	1	1	0	0	1	1	1
4	0	0	0	1	1	1	1	1
5	0	0	0	1	1	1	1	1
6	0	0	0	0	0	1	1	1
7	0	0	0	0	0	0	1	1
8	0	0	0	0	0	0	1	1

Матрица контрдостижимости Q_G :

	1	2	3	4	5	6	7	8
1	1	1	1	0	0	0	0	0
2	1	1	1	0	0	0	0	0
3	1	1	1	0	0	0	0	0
4	0	0	0	1	1	0	0	0
5	0	0	0	1	1	0	0	0
6	1	1	1	1	1	1	0	0
7	1	1	1	1	1	1	1	1
8	1	1	1	1	1	1	1	1

М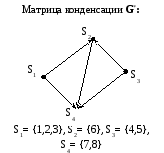атрица взаимной достижимостиS_G :

	1	2	3	4	5	6	7	8
1	1	1	1	0	0	0	0	0
2	1	1	1	0	0	0	0	0
3	1	1	1	0	0	0	0	0
4	0	0	0	1	1	0	0	0
5	0	0	0	1	1	0	0	0
6	0	0	0	0	0	1	0	0
7	0	0	0	0	0	0	1	1
8	0	0	0	0	0	0	1	1

Для базы:

1. Выделим в конденсации вершины с нулевыми полустепенями захода.

Базовые компоненты:S₁ иS₃.

2. Базы орграфа G: {1,4}; {1,5}; {2,4}; {2,5}; {3,4}; {3,5}.

Для антибазы:

1. Выделить в конденсации вершины с нулевыми полустепенями исхода.

Антибазовые компоненты:S₄.

2. Антибаза орграфа G: {7}; {8}.