Маршруты в орграфах

Ориентированный маршрут(ормаршрут) – конечная чередующаяся последовательность вершин и дуг графа таких, что каждая дуга исходит из предыдущей вершины и заходит в последующую вершину a_i= (v_i-1 , v_i) :

Орцепь – ориентированный маршрут без повторяющихся дуг.

Путь –цепь без повторяющихся вершин .

Ориентированный цикл – замкнутая ориентированная цепь.

Контур – замкнутый путь или замкнутый маршрут без повторения дуг и вершин(кроме, возможно, крайних).

Длина ориентированного маршрута– число дуг, составляющих маршрут, с учетом повторения.

Полумаршрут (маршрут основания) – последовательность вершин и дуг орграфа, что a_i= (v_i-1 , v_i) или (v_i , v_i+1).

Аналогично вводятся понятия полуцепь, полупуть, полуконтур.

Типы связности графа

Вершина vграфаG достижимаиз вершиныu, если существует (u,v)- маршрут вG, соответственно вершинаu – контрдостижима для вершины v. Любая вершина считается достижима для самой себя.

Вершины v иuграфаG – взаимнодостижимы, если вершина v достижима для вершины u, и вершина u достижима для вершины v.

Орграф G – сильносвязный (сильный), если любые две вершины в нём взаимнодостижимы.

Орграф G – одностороннесвязный (односторонний), если для каждой пары его вершин, по крайней мере, одна достижима из другой.

Орграф G – слабосвязный (слабый), если любые две его вершины соединены полумаршрутом (полупутем).

Орграф G – несвязен, если несвязно его основание.

Сильная компонента – максимальный относительно включения сильный подграф исходного орграфа.

Односторонняя компонента – максимальный относительно включения односторонний подграф исходного орграфа.

Слабая компонента – максимальный относительно включения слабый подграф исходного орграфа.

Например:

Слабый орграф

Орграф является сильным тогда и только тогда, когда в нём есть остовный циклический маршрут.

Орграф является односторонним тогда и только тогда, когда в нём есть остовный маршрут.

Орграф является слабым тогда и только тогда, когда в нём есть остовный полумаршрут.

Остовный маршрут– маршрут, содержащий все вершины исходного графа.

Конденсация орграфа

Конденсация орграфа G – орграфG^*,вершиныS₁, S₂, …, S_m которого соответствуют сильным компонентам орграфаGи дуга (S_i, S_j) принадлежит орграфу G^* тогда и только тогда, когда в G существует дуганачало которой находится в сильной компоненте S_i, конец – вS_j.

Например:

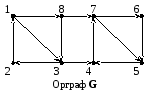
Конденсация G^* любого орграфа не имеет контуров.

Алгоритм построения конденсации

1. Построим матрицу достижимости орграфа G.

R=||r_ij||, где i,j = 1..p .

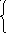1, еслиi достижима для j;

r_ij =

0, иначе

Построим матрицу контрдостижимости

Q=||q_ij||,где i,j= 1..p , Q = R^T.

1, если i контрдостижима для j;

q_ij =

0, иначе.

2. Найдем матрицу взаимной достижимости, где “ * ”– оператор поэлементного умножения матриц.

S=R*Q=R*R^T,

s_ij=r_ij*q_ij , i,j = 1..p.

3. Выберем некоторую вершину v_i V,тогда сильная компонента орграфа, содержащаяv_i, определяется единичными элементамиi-той строки матрицыS, или перестановкой строк и столбцов можно привести матрицуSк блочно-диагональному виду, где каждый блок будет соответствовать некоторой сильной компоненте орграфаG.

Например:

Задан граф G. Построить конденсациюG^*.

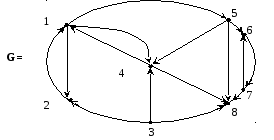
Решение:

Матрица достижимости R_G :

	1	2	3	4	5	6	7	8
1	1	1	0	1	1	1	1	1
2	1	1	0	1	1	1	1	1
3	1	1	1	1	1	1	1	1
4	1	1	0	1	1	1	1	1
5	1	1	0	1	1	1	1	1
6	0	0	0	0	0	1	1	1
7	0	0	0	0	0	1	1	1
8	0	0	0	0	0	0	0	1

Матрица контрдостижимости Q_G :

	1	2	3	4	5	6	7	8
1	1	1	1	1	1	0	0	0
2	1	1	1	1	1	0	0	0
3	0	0	1	0	0	0	0	0
4	1	1	1	1	1	0	0	0
5	1	1	1	1	1	0	0	0
6	1	1	1	1	1	1	1	0
7	1	1	1	1	1	1	1	0
8	1	1	1	1	1	1	1	1

Матрица взаимной достижимостиS_G:

	1	2	3	4	5	6	7	8
1	1	1	0	1	1	0	0	0
2	1	1	0	1	1	0	0	0
3	0	0	1	0	0	0	0	0
4	1	1	0	1	1	0	0	0
5	1	1	0	1	1	0	0	0
6	0	0	0	0	0	1	1	0
7	0	0	0	0	0	1	1	0
8	0	0	0	0	0	0	0	1