
Методичні вказівки до курсової роботи з дисципліни Алгоритмізація розрахунків в хімічній технології
.pdfМІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ДЕРЖАВНИЙ ВИЩИЙ НАВЧАЛЬНИЙ ЗАКЛАД
ДОНЕЦЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ
МЕТОДИЧНІ ВКАЗІВКИ
до курсової роботи з дисципліни
«Алгоритмізація розрахунків в хімічній технології»
для студентів напряму підготовки 6.051301 «Хімічна технологія»
Розглянуто на засіданні кафедри хімічної технології палива, протокол № 1 від 6.09.2010 р.
Затверджено на засіданні навча- льно-видавничої ради ДонНТУ, протокол № 1 від 13.01.2011 р.
Донецьк, 2011 р.
2
Методичні вказівки до курсової роботи з дисципліни «Алгоритміза-
ція розрахунків в хімічній технології» ( для студентів напряму підготов-
ки 6.051301 «Хімічна технологія») / Складачі: О.І. Збиковський, Є.І.
Збиковський. – Донецьк, ДонНТУ, 2011. – 18 с.
В методичних вказівках приведені тема, ціль і задачі, які вирішує курсова робота. Сформульована постанова задачі, яку повинні розв’язати студенти, дані вказівки по побудові алгоритму і комп’ютерної програми. Приведений зміст курсової роботи. Викладена сутність чисельних методів інтегрування, за допомогою яких треба розв’язати поставлену задачу. Приведені 40 варіантів завдання і перелік рекомендованої літератури. У додатку приведені перелік, найменування, позначення і розміри основних блочних символів, що використовуються для складання блок-схем.
Складачі: О.І. Збиковський, доц. каф. ХТП Є.І. Збиковський, доц. каф. ХТП
Відповідальний за випуск: Л.Ф. Бутузова, проф., зав. каф. ХТП
3
1 ТЕМА І ЦІЛЬ КУРСОВОЇ РОБОТИ
Навчальними планами для студентів напряму підготовки 6.051301
передбачено виконання курсової роботи з дисципліни «Алгоритмізація
розрахунків в хімічній технології».
Тема курсової роботи: «Чисельне інтегрування методами прямокутників, трапецій, Сімпсона і Монте-Карло».
Ціль курсової роботи – вивчити сутність чисельного інтегрування методами прямокутників, трапецій, Сімпсона і Монте-Карло, скласти блок-схему алгоритму розрахунку і програму розрахунку на мові Turbo Pascal 7.0 визначеного інтегралу цими методами, виконати розрахунок визначеного інтегралу за допомогою складеної програми, провести аналіз отриманих результатів.
Задачі курсової роботи – навчити студентів чисельному інтегруванню методами прямокутників, трапецій, Сімпсона і Монте-Карло з використанням комп’ютера:
-оволодіти сутністю методів;
-скласти блок-схему алгоритму і програму розрахунку на мові
Turbo Pascal 7.0;
-провести налагодження програми і виконати розрахунок визначеного інтегралу;
-проаналізувати отримані результати і зробити висновки.
2 ПОСТАНОВА ЗАДАЧІ
b
Необхідно розрахувати визначений інтеграл f (x) dx із заданою
a
похибкою методами прямокутників, трапецій, Сімпсона і МонтеКарло.
Алгоритм розрахунку за кожним методом треба побудувати наступним чином:
1)для розрахунку першого приблизного значення інтеграла відрізок інтегрування розбивається на n рівних частин (для методу Монте-Карло береться n випадкових точок);
2)значення n збільшується в 2 рази, після чого розраховується наступне приблизне значення визначеного інтегралу;
3)розраховується модуль різниці поточного і попереднього значень визначеного інтеграла і порівнюється із заданою похибкою
:
4
-якщо модуль різниці менше або дорівнює , то вважається, що інтеграл розрахований із заданою похибкою (тобто розрахунок закінчується);
-якщо модуль різниці більше , то розраховується наступне приблизне значення інтеграла (тобто здійснюється повернення на
пункт 2).
Розрахунок за кожним методом в алгоритмі представити у вигляді окремої підпрограми з набором наступних формальних параметрів:
а – ліва межа відрізка інтегрування; b – права межа відрізка інтегрування;
n – кількість рівних частин, на яку розбивається відрізок інтегрування (для методу Монте-Карло кількість випадкових точок) ;
– задана похибка.
Результати розрахунку за кожним методом представити у вигляді таблиці, перша колонка якої повинна містити значення n, а друга – розраховане приблизне значення інтеграла при відповідному значенні n.
Скласти програму і два модулі на мові Turbo Pascal 7.0: перший модуль використати для зберігання оголошень змінних, констант і користувальницьких типів, другий – для зберігання підпрограм.
В програмі організувати файлове введення вихідних даних і файлове виведення результатів.
3 ЗМІСТ КУРСОВОЇ РОБОТИ
Вступ 1 Постанова задачі
2 Сутність методів чисельного інтегрування, їх похибка
2.1 Метод лівих прямокутників
2.2 Метод правих прямокутників
2.3 Метод середніх прямокутників
2.4 Метод трапецій
2.5 Метод Сімпсона
2.6Метод Монте-Карло
2.7Похибка методів
3Блок-схема алгоритму розрахунку
4Ідентифікації змінних
5Програма розрахунку на мові Turbo Pascal 7.0
6Вихідні дані і результати розрахунку
7Аналіз результатів
Висновки Перелік посилань
5
4 СУТНІСТЬ МЕТОДІВ ЧИСЕЛЬНОГО ІНТЕГРУВАННЯ
Потрібно розрахувати визначений інтеграл:
.
Відомо, що для неперервної на відрізку , функції визначений інтеграл можна розрахувати за формулою Ньютона-Лейбніца:
= − ,
де ( ) – первісна функції ( ).
Необхідність застосування чисельного інтегрування найчастіше може бути викликана відсутністю у первісної функції подання в елементарних функціях і, отже, неможливістю аналітичного обчислення значення визначеного інтеграла за формулою Ньютона-Лейбніца. Також можлива ситуація, коли вид первісної настільки складний, що швидше обчислити значення інтеграла чисельним методом.
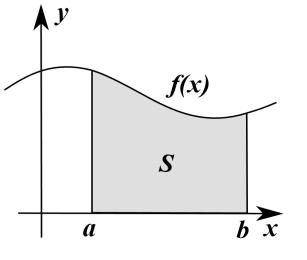
Чисельне інтегрування – обчислення значення визначеного інтеграла (як правило, наближене), засноване на тому, що величина інтеграла чисельно дорівнює площі криволінійної трапеції – фігури, обмеженої віссю абсцис, прямими = і = і графіком підінтегральної функції
( ) (рис. 4.1).
Рисунок 4.1 – Криволінійна трапеція
6
Сутність більшості методів обчислення визначеного інтегралу полягає в апроксимації підінтегральної функції ( ) функцією ( ), для якої легко можна записати первісну в елементарних функціях і обчислити інтеграл аналітично:
|
|
= + = + ,
|
|
де = – приблизне значення інтегралу,
R– похибка обчислення інтегралу.
Взалежності від способу апроксимації підінтегральної функції методи чисельного інтегрування поділяються на групи.
Методи прямокутників, трапецій і Сімпсона відносяться до групи методів Ньютона-Котеса, в основі яких лежить апроксимація підінтегральної функції ступеневим багаточленом. Методи відрізняються один від одного ступенем використаного багаточлена, від якого залежить кількість вузлів, в котрих необхідно розрахувати підінтегральну функцію ( ).
Вгрупі методів Монте-Карло вузли, в яких розраховується значення підінтегральної функції ( ), вибираються за допомогою генератора випадкових чисел. При цьому значення розрахованого інтеграла має імовірнісний характер.
4.1 Методи прямокутників
В методах прямокутників підінтегральна функція ( ) апроксимується ступеневим багаточленом нульового ступеня = 0 0, тобто горизонтальною прямою.
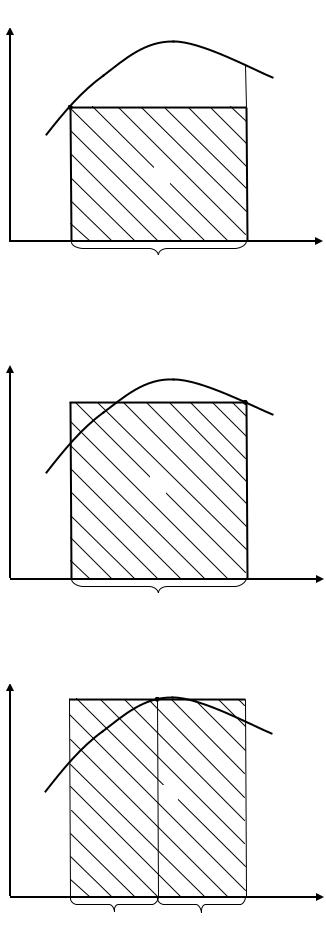
Наближене значення визначеного інтеграла розраховується як площа прямокутника, одна зі сторін якого є відрізком інтегрування, а інша – значенням функції в лівій межі відрізка інтегрування для методу лівих прямокутників, в правій межі відрізка інтегрування для методу правих прямокутників і в середині відрізка інтегрування для методу середніх прямокутників (рис. 4.2 – 4.4).
7
R |
= |
S
a |
h |
b |
|
|
Рисунок 4.2 – Метод лівих прямокутників
=
S
a |
h |
b |
|
|
Рисунок 4.3 – Метод правих прямокутників
=
S
a |
|
|
|
b
Рисунок 4.4 – Метод середніх прямокутників
8
Формула лівих прямокутників для одного відрізка:
= − ∙ ( ) + = ∙ ( ) + .
Формула правих прямокутників для одного відрізка:
= − ∙ ( ) + = ∙ ( ) + .
Формула середніх прямокутників для одного відрізка:
= − ∙ + |
|
+ = ∙ + |
|
+ . |
|
|
|||
2 |
2 |
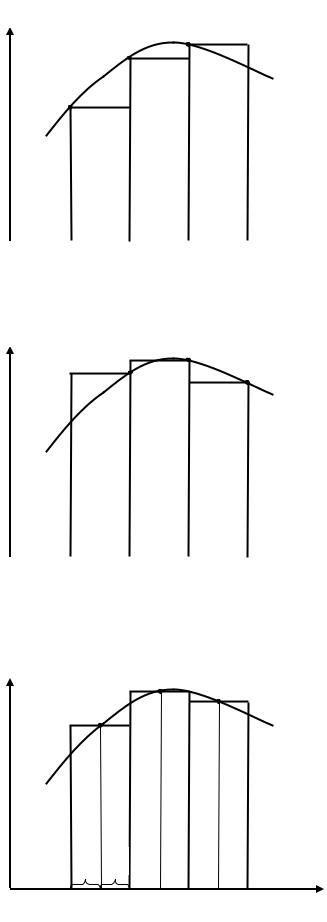
Для зменшення похибки розрахунку інтеграла відрізок інтегрування розбивають на n зазвичай рівних відрізків і на кожному з них будують прямокутник (рис. 4.5 – 4.7).
Тоді наближене значення інтеграла буде дорівнювати сумі площ n прямокутників, побудованих на відрізку інтегрування.
Формула лівих прямокутників для n відрізків:
|
−1 |
|
−1 |
|
||
= |
− |
∙ |
|
+ = ∙ |
|
+ . |
|
||||||
|
|
|
|
|
|
|
|
=0 |
|
=0 |
|
||
|
|
|
||||
Формула правих прямокутників для n відрізків:
|
|
|
|
|
||
= |
− |
∙ |
|
+ = ∙ |
|
+ . |
|
||||||
|
|
|
|
|
|
|
|
=1 |
|
=1 |
|
||
|
|
|
||||
Формула середніх прямокутників для n відрізків:
|
|
− |
|
−1 |
|
|
|
+ = ∙ −1 |
|
|
|
|
|
|
= |
∙ |
|
+ |
|
+ |
+ . |
||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
2 |
|
|
|
2 |
|
||
|
|
=0 |
|
|
=0 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||
Чим менше довжина відрізків, на які ділиться відрізок інтегрування, тим точніше значення інтеграла, яке обчислюється за цими формулами.
Апріорна оцінка похибки обчислення інтеграла методами лівих і правих прямокутників:
9
=

х0 = а х1 х2 х3 =
Рисунок 4.5 – Метод лівих прямокутників для трьох відрізків
=

х0 = а х1 х2 х3 =
Рисунок 4.6 – Метод правих прямокутників для трьох відрізків
=
|
|
|
|
|
|
х0 = а х1 х2 х3 =
Рисунок 4.7 – Метод середніх прямокутників для трьох відрізків
10
= |
|
∙ |
|
|
. |
|
|||||
2 |
|||||
|
|
|
|
|
|
Апріорна оцінка похибки обчислення інтеграла методом середніх прямокутників:
|
2 |
|
|
|
|
|
|
|
|
||
= |
|
∙ |
|
|
. |
24 |
|||||
Ступінь кроку інтегрування називається порядком точності методу інтегрування. Отже методи лівих і правих прямокутників мають перший порядок точності, а метод середніх прямокутників – другий.
4.2 Метод трапецій |
|
|
|
|
В методі трапецій підінтегральна функція |
( ) апроксимується |
|||
ступеневим багаточленом першого ступеня |
= |
0 |
0 + 1, тобто |
|
|
|
|
1 |
|
прямою, яка проходить через дві точки , |
і , |
на кінцях |
||
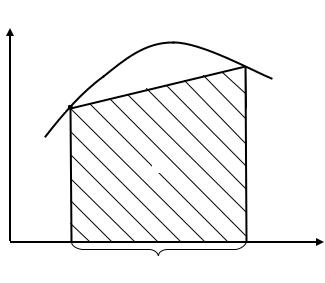
відрізка інтегрування (рис. 4.8). |
|
|
|
|
R  B
B
=
А
S
a |
h |
b |
|
|
Рисунок 4.8 – Метод трапецій
Наближене значення визначеного інтеграла розраховується як площа прямокутної трапеції, нижня сторона якої є відрізком інтегрування, ліва бокова – значенням підінтегральної функції в лівій межі відрізка інтегрування, права бокова – значенням підінтегральної функції в правій межі відрізка інтегрування, верхня – відрізком апроксимуючої прямої.
