13

Лабораторная работа №

Орграфы.

Цель работы: изучение основных понятий орграфов. Получение практических навыков нахождения сильных компонент, построения конденсации, базы и антибазы.

Теоретическая справка Определение ориентированного графа (орграфа)

Ориентированный граф G =(V,A) – пара множествV иA, таких, чтоV – некоторое конечное непустое множество, аA – некоторое подмножество декартового квадратаV(A  V² =V*V) .

ВершиныграфаG– элементы множестваB .

Дуги графа G – элементы множества A.

Дуга –упорядоченная пара вершин a=(u,v).

Начало дуги – вершина u, конец дуги – вершина v.

Дуга исходитиз своего начала изаходитв свой конец.

Орграф G – орграф p-го порядка, если мощность множества|V|=p.

Способы описания орграфов

1. Матрица смежности.

A=||a_ij||, i,j=1.. p, |V|=p, |A|=q.

1, если существует дуга (i,j) ;

a_ij =

0, иначе .

2. Матрица инцидентности.

B=||b_ij||, i=1.. p, j=1.. q, |A|=q, |V|=p.

1, i – начало дуги j;

b_ij = -1, i – конец дуги j;

0, иначе.

Например:

Орграф G(V,A)

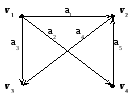
Матрица инцидентности:

	a1	a2	a3	a4	a5
BG= v1	1	1	1	0	0
v2	-1	0	0	1	-1
v3	0	0	-1	-1	0
v4	0	-1	0	0	1

Матрица смежности:

	v1	v2	v3	v4
AG= v1	0	1	1	1
v2	0	0	1	0
v3	0	0	0	0
v4	0	1	0	0

Основание - неориентированный граф, получившийся в результате снятия ориентации дуг орграфа.

Обратный графG^-1=(V,A^-1) – орграф,у которого множество вершин совпадает с исходным графом, и дуга (u ,v) A^-1  (v,u) A.

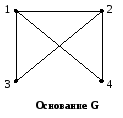
Турнир – ориентированый граф, основание которого есть полный граф.

Степени вершин орграфа

Полустепень захода вершины vграфаG –число дуг, заходящих в вершинуv:

deg ^– (v) = | X | ; X = { x | x = (u,v) A}.

Полустепень исхода вершины vграфаG– число дуг, исходящих из вершиныv:

deg ⁺ (v) = | Y | ; Y = { y | y = (v,u) A}.

Степень вершины vграфаG– сумма полустепеней захода и исхода в вершинеv: deg (v) = deg ⁺ (v) + deg ^– (v).

Сумма полустепеней захода всех вершин орграфа G равна сумме полустепеней исхода, и равна количеству дуг.