Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Донецкий национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Методичні вказівки до курсової роботи з дисципліни Алгоритмізація розрахунків в хімічній технології

.pdf

Скачиваний:

Добавлен:

03.03.2016

Размер:

1.21 Mб

Скачать

☆

<<< < Предыдущая 12 / 22

Формула трапецій для одного відрізка:

= − ∙	+	+ = ∙	+	+ .
	2		2

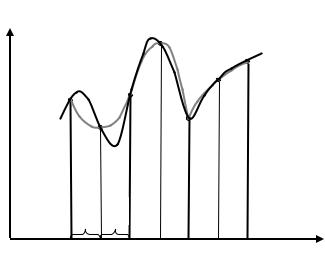
Також як і для методів прямокутників для зменшення похибки розрахунку інтеграла відрізок інтегрування розбивають на n рівних відрізків і на кожному з них будують прямокутну трапецію (рис. 4.9).

х0 = а х1 х2 х3 =

Рисунок 4.9 – Метод трапецій для трьох відрізків

Наближене значення інтеграла буде дорівнювати сумі площ n прямокутних трапецій, побудованих на відрізку інтегрування.

Формула трапецій для n відрізків:

−

−1(

∙

) + =

∙

) + .

2 ∙

Апріорна оцінка похибки обчислення інтеграла методом трапецій:

	2

= −		∙	.
	12

Отже метод трапецій має другий порядок точності.

4.3 Метод Сімпсона

В методі Сімпсона підінтегральна функція ( ) апроксимується ступеневим багаточленом другого ступеня = 0 0 + 1 1 + 2 2,

тобто параболою, яка проходить через три точки , , ,

і С +		,	+		(рис. 4.10).
	2			2

	С
	С
=	B	=
А



	+
	+	2
		2

Рисунок 4.10 – Метод Сімпсона

Наближене значення визначеного інтеграла розраховується як площа так званої параболічної трапеції – криволінійної трапеції, яка зверху обмежена параболою.

Формула Сімпсона для одного відрізка:

		−				+
=				∙ + 4 ∙				+		+ =

			6				2

=			∙ + 4 ∙ +				+		+ .

	6				2

Для зменшення похибки розрахунку інтеграла відрізок інтегрування розбивають на n рівних відрізків і на кожному з них будують па-

раболічну трапецію (рис. 4.11).

Наближене

значення інтеграла буде дорівнювати сумі площ n па-

раболічних трапецій, побудованих на відрізку інтегрування.

Формула Сімпсона для n відрізків:

−

−1

∙

+ 4 ∙

+ =

6 ∙

∙ −1

+ 4 ∙

+ .

=		=
		=

х0 = а х1 х2 х3 =

Рисунок 4.11 – Метод Сімпсона для трьох відрізків

Апріорна оцінка похибки обчислення інтеграла методом Сімпсо-

на:

	4

= −		∙	.
	180

Отже метод Сімпсона має найвищий четвертий порядок точності.

4.4 Метод Монте-Карло

Розглянемо один з методів Монте-Карло, який можна інтерпретувати як статистичний варіант методу прямокутників.

Береться n випадкових точок , рівномірно розподілених на відрізку інтегрування , . В кожній з них розраховується значення підінтегральної функції ( ). Після чого розраховується середнє значення підінтегральної функції:

=	1	∙	.
=		∙	.
ср

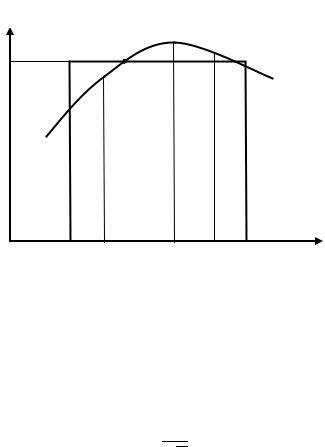
Наближене значення визначеного інтеграла розраховується як площа прямокутника, одна зі сторін якого є відрізком інтегрування, а інша – середнім значенням підінтегральної функції ср (рис. 4.12):

			−
= − ∙		+ =		∙	+ .
	ср

ср

	2

1


	1	2

Рисунок 4.12 – Метод Монте-Карло

Так як у методі Монте-Карло використовуються випадкові числа, то і похибка обчислення інтеграла буде мати випадковий характер. Вона залежить тільки від кількості випадкових точок:

~ 1 .

4 ВАРІАНТИ ЗАВДАННЯ

№			Інтеграл								№				Інтеграл

		8										0,6			tg( 2 + 0,5)
1				2					4	0,0001	5				tg( 2 + 0,5)	4	0,0002

	0,1	tg						2 + 4				0,2			1 + 2 2
		tg						2 + 4							1 + 2 2

		2										1,2		sin( 2 − 0,4)
		lg ( + 2)												sin( 2 − 0,4)
2									3	0,0002	6					3	0,0001
2	1,2								3	0,0002	6	0,8			+ 2	3	0,0001
															+ 2

		1,2										0,6
3					sin 2				2	0,0003	7				sin( + 1,4)	2	0,0003

		0,8					2					0,2	cos(2 2 + 0,5)
		0,8										0,2
		1,2					cos					0,4
4							cos		5	0,0001	8		10−2 2 + 1			5	0,0001
4		0,4				+ 2			5	0,0001	8		10−2 2 + 1			5	0,0001
						+ 2
												0

№						Інтеграл													№						Інтеграл

				1																	1
																													2
9										− 1							3	0,0002	20										2				2	0,0002
		0,1																			0
				1,2																	2
10																	4	0,0001	21		1												4	0,0001

																					1						sin 2
																											sin 2
				1
		0,8																			1
												cos 2															2 −2
11												cos 2					5	0,0003	22								2 −2						5	0,0004
		0,1																			0,2

	0,6																				0,9								tg 2
12																	3	0,0002	23														3	0,0002

	0,1				+ 1 lg ( + 3)																0,2							2 + 1
					+ 1 lg ( + 3)																							2 + 1

				3																2					1 + 1,2 2
																									1 + 1,2 2
13											lg						4	0,0001	24														5	0,0001
13											lg						4	0,0001	24														5	0,0001
				1,4																1,2	0,8 +									2 + 1,3
				1,4																1,2

		1																			1,6				lg ( 2 + 1)
			( + 1) cos 2																						lg ( 2 + 1)
14																	2	0,0001	25														2	0,0003
14																	2	0,0001	25										+ 1				2	0,0003
	0,2																				0,8								+ 1
	0,2																				0,8
		2																		1,8				sin( 2 − 0,4)

						+ 1 cos 2
15																	3	0,0002	26														4	0,0002
15	0,2																3	0,0002	26	0,8									+ 2				4	0,0002
																													+ 2


	1,4																			0,8
										2 + 5													sin(2 + 0,5)
16																	4	0,0001	27														4	0,0001
																						2 + cos( 2										+ 1)
			2 +												2							2 + cos( 2										+ 1)
	0,6		2 +													+ 0,5				0,2
		2,5																			2,2				lg ( 2 + 3)
											1														lg ( 2 + 3)
17																	5	0,0003	28														5	0,0001
17																	5	0,0003	28										2				5	0,0001
							0,2							2		+ 1													2
	1,3						0,2									+ 1					1,2
	1,3																				1,2
				−1,3									2								2
				−1,3																	2					0,6 + 1,5
																										0,6 + 1,5
18																	3	0,0002	29														2	0,0002
18									1 − 4								3	0,0002	29														2	0,0002
									1 − 4											0,7			2 + 2								+ 3
			−2																	0,7
				2,5																	2,7				lg ( 2 + 2)
											1														lg ( 2 + 2)
19																	4	0,0001	30														4	0,0001
19				2				ln2									4	0,0001	30		0,7								+ 1				4	0,0001
								ln2																					+ 1

№				Інтеграл									№				Інтеграл

	2,6				1 + 0,6 2									2		sin( 2 − 1)
					1 + 0,6 2											sin( 2 − 1)
31												2	36						4	0,0002
31												2	36	2					4	0,0002
		1,9 +							0,7	2	+ 1,5			2
	1,3	1,9 +							0,7		+ 1,5			1,3
	2,5													1
	2,5				0,8 2 + 1,3									1	sin( + 1,4)
					0,8 2 + 1,3										sin( + 1,4)
32												4	37						2	0,0001
32												4	37		0,8 + cos(2 2 + 5)				2	0,0001
	1,4	1,4 +						2 + 0,6						0,4	0,8 + cos(2 2 + 5)
	1,4													0,4
		2,4												2,5
33							1					3	38				2 + 1	lg	5	0,0004


	1,4					2 2 + 0,7								1,4
	1,4													1,4
	2,5		lg ( 2											1,3
34			lg ( 2				+ 2,5)					3	39		2 + 0,5			sin	2	0,0002
34	1					2 + 1						3	39	0,4	2 + 0,5			sin	2	0,0002
						2 + 1

	3,7		lg ( 2											1,6			ln ( 2 + 1)
			lg ( 2				+ 0,8)										ln ( 2 + 1)
35												4	40						3	0,0001
35	2					− 1						4	40	0,8					3	0,0001
						− 1

5ПЕРЕЛІК РЕКОМЕНДОВАНОЇ ЛІТЕРАТУРИ

1.Мудров А.Е. Численные методы для ПЭВМ на языке Бейсик, Фортран и Паскаль. – Томск: м.п. “Раско”, 1993. – 272 с.

2.Турчак Л.И., Плотников П.В. Основы численных методов. – М.: ФИЗМАТЛИТ, 2003. – 304 с.

3.Брановицька С.В., Медведєв Р.Б., Фіалков Ю.Я. Обчислювальна математика та програмування: Обчислювальна математика в хімії і хімічній технології. – К.: ІВЦ «Видавництво «Політехніка», ТОВ «Фірма «Періодика», 2004. – 220 с.

4.Калиткин Н.Н. Численные методы. – М.: Наука, 1978. – 512 с.

5.Мак-Кракен Д., Дорн У. Численные методы и программирование на Фортране. – М.: Мир, 1977. – 584 с.

6.Данилина Н.И., Дубровская Н.С., Кваша О.П., Смирнов Г.Л. Вычислительная математика. – М.: Высш. школа, 1985. – 472 с.

7.Эберт К., Эдерер Х. Компьютеры. Применение в химии. – М.: Мир, 1988. – 416 с.

8.Епанешников А.М., Епанешников В.А. Программирование в среде Turbo

Pascal 7.0. – М.: "Диалог–МИФИ", 1998. – 367 с.

ДОДАТОК А

ПЕРЕЛІК, НАЙМЕНУВАННЯ І ПОЗНАЧЕННЯ СИМВОЛІВ І ФУНКЦІЇ, ЯКІ ВОНИ ВІДОБРАЖАЮТЬ

Перелік, найменування, позначення і розміри основних обов’язкових

ірекомендованих символів і функції, які вони відображають в алгоритмі

іпрограмі обробки даних, повинні відповідати вказаним в таблиці.

Найменування

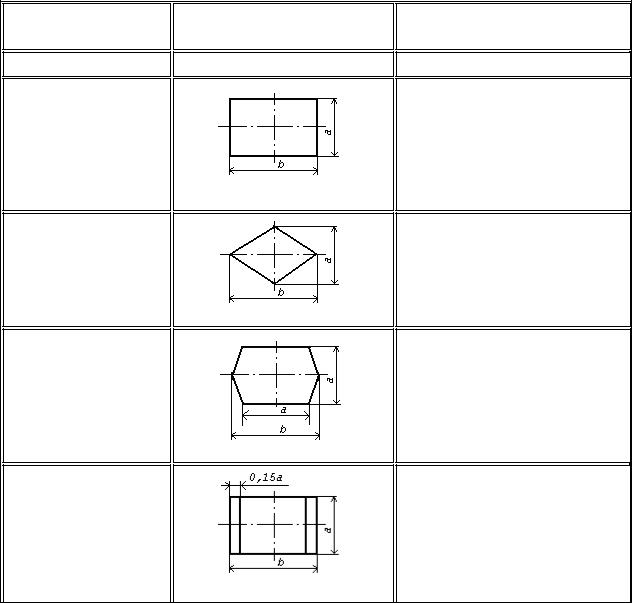
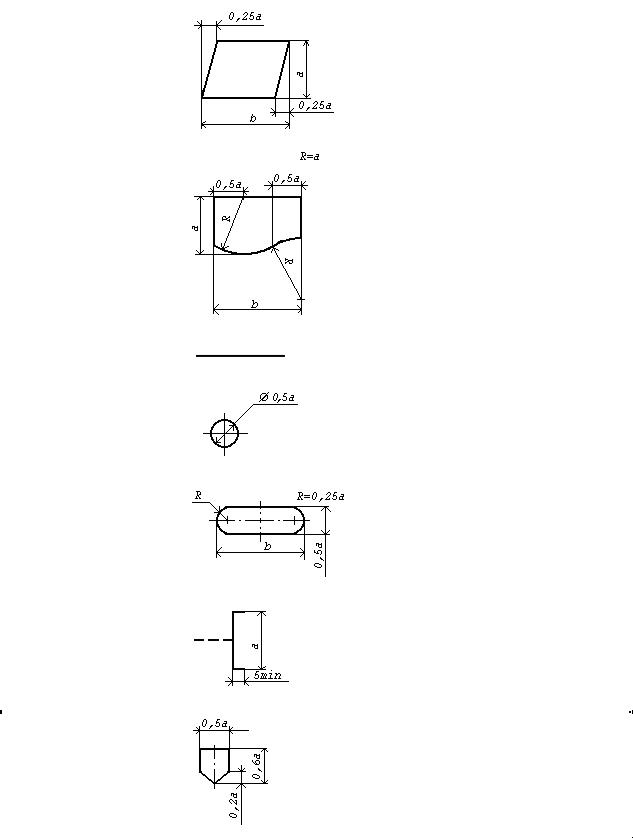
1. Процес

Позначення і розміри

вмм

2.Рішення

3.Модифікація

4.Зумовлений

процес

Функція

Виконання операцій або груп операцій, в результаті яких змінюється значення, форма представлення або розташування даних

Вибір напрямку виконання алгоритму або програми в залежності від деяких змінних умов

Виконання операцій, які змінюють команди або групу команд, що змінюють програму

Використання раніше створених і окремо описаних алгоритмів або програм

		18

1		2			3

			Перетворення даних в фо-
	5. Введення-		рму, яка придатна для об-
	5. Введення-		робки (введення) або відо-
	виведення		робки (введення) або відо-
	виведення		браження		результатів		об-
			браження		результатів		об-
			робки (виведення)


	6. Документ		Введення-виведення да-
	6. Документ		них, носієм яких є папір
			них, носієм яких є папір


	7. Лінія потоку		Вказівка послідовності
	7. Лінія потоку		між символами
			між символами

			Вказівка зв’язку між пере-
	8. З’єднувач		рваними		лініями	потоку,
			які зв’язують символи


			Початок, кінець, перери-
	9. Пуск - зупинка		вання	процесу		обробки
	9. Пуск - зупинка		даних або виконання про-
			даних або виконання про-
			грами


	10. Коментар		Зв’язок між елементом
	10. Коментар		схеми і поясненням
			схеми і поясненням

			Вказівка		зв’язку		між
	11. Межсторінковий		роз’єднаними частинами
	11. Межсторінковий		схем	алгоритмів		і	про-
	з’єднувач		схем	алгоритмів		і	про-
	з’єднувач		грам, розташованих на рі-
			грам, розташованих на рі-
			зних листах

Розмір a повинен вибиратися з ряду 10, 15, 20 мм. Допускається збільшувати розмір a на число, кратне 5. Розмір b дорівнює 1,5a. При ручному виконанні схем алгоритмів і програм допускається встановлювати b рівним 2a.

<<< < Предыдущая 12 / 22

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
03.03.20162.18 Mб49Методичка_курсовая_15.doc
#
03.03.2016119.3 Кб4Методичка_Курсовой_ новая.doc
#
03.03.20161.61 Mб44Методичка_Структурная Геология.pdf
#
03.03.20161.93 Mб2методичкаМЧМ,МКМ, ПТТ(ТП), ОМТ.rtf
#
03.03.20161.26 Mб28методички 2015.pdf
#
03.03.20161.21 Mб4Методичні вказівки до курсової роботи з дисципліни Алгоритмізація розрахунків в хімічній технології.pdf
#
03.03.2016875.32 Кб6Методичні вказівки до лабораторних робіт з дисципліни Алгоритмізація розрахунків в хімічній технології.pdf
#
03.03.20161.16 Mб18Методична розробка на КП 2012.pdf
#
03.03.2016114.04 Кб57Методрекомендации по оформлению ПЭР.docx
#
03.03.2016183.3 Кб13Методчика - Орграфы.doc
#
03.03.20165.1 Mб198Методы и средства защиты информации.pdf