Тема 3. Машины тьюринга
Рекурсивные функции представляют алгоритм через вычислимую функцию, т.е. понятие « вычислимая функция » является первичным по отношению к понятию « алгоритм ». Машины Тьюринга (МТ) являются в этом смысле более естественными, т.к. вначале уточняют понятие « алгоритм », а через него – вычислимую функцию.
Машина Тьюринга (Тьюринга-Поста, т.к. предложена ими почти одновременно и независимо в 1936-1937 гг.) построена на основе использования свойства детерминированности алгоритмов. Основной смысл этого свойства сводится к тому, что алгоритмический процесс должен выполнятся механически, т.е. может быть реализован машиной. Машина Тьюринга является абстрактной, т.к. имеет неограниченные ресурсы, что требуется для реализации любых алгоритмов.
В данной теме вводятся некоторые понятия символьных конструкций и операций над ними, описаны функционирование и способы задания МТ, способы композиции МТ, позволяющие строить сложные МТ из более простых, приводится понятие об эквивалентности МТ и рекурсивных функций.
Наиболее полно ( в рамках программы курса ) машины Тьюринга описаны в [ 1,4,8 ] , приводится большое количество примеров. В [2] изложение более популярное и менее формализованное. Дополнительный материал о МТ можно найти в [7].
Задания на самостоятельную работу
Контрольные вопросы :
- определение машины Тьюринга;
- какие операции выполняются в каждом такте работы МТ ?
- назовите способы описания работы МТ;
- что такое функция, правильно вычислимая по Тьюрингу ?
- какие способы композиции МТ существуют, как они применяются ?
- формулировка тезиса Тьюринга; можно ли его доказать строго ?
Опишите системой команд, функциональной таблицей и диаграммой переходов работу машин Тьюринга, выполняющих :
а) прибавление 1 к числу в десятичной системе счисления;
б)
операцию арифметическое вычитание
в
унарном коде;
в) выбор максимального из двух чисел, записанных на ленте в унарном коде;
г) сдвиг вправо на одну ячейку двоичного числа;
д)
перевод слова
в слово
е)
перевод слова
в слово
ж)
вычисление функции
з)
в слове
в алфавите
замену
всех вхождений буквыа
на букву б.
и)
копирование слова
в алфавите
т.е.
получение из слова
слова *;
к)
выделение из слова
в алфавите
подслова, заключенного между звездочками;
если пары звездочек нет, МТ работает бесконечно;
л) вычисление предиката X>Y в унарном коде;
м) вычисление предиката X=Y в унарном коде;
н) вычисление предиката « Х - четное число » в двоичном коде;
о)
вычисление предиката « в слове
в алфавите
есть
пара букв ‘yy’ »
п)
вычисление логической функции
,
гдеx,y,z
принимают
значение 0 или 1;
р)
вычисление логической функции
,
гдеx,y,z
принимают
значение 0 или 1;
Приведите последовательность конфигураций каждой из МТ, заданных в предыдущем пункте для исходных слов, заданных преподавателем. Начальная конфигурация стандартна.
Выясните, путем построения последовательности конфигураций, применима ли машина
,
заданная системой команд
,
к слову.
Если применима, то найти результат.
Начальная конфигурация стандартна.
а)
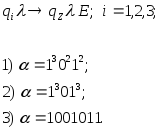
б)
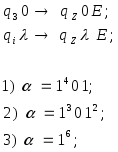
в)
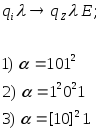
Построить композиции МТ, реализующие следующие алгоритмы над числами в унарном коде ( в схеме композиции необходимо перед и после каждой МТ указывать, какое слово записано на ленте );
а) вычисление x+y с использованием операции прибавления 1;
б) вычисление n!;
в) получение частного [x/y] и остатка;
г) алгоритм Евклида;
д) возведение в степень с использованием операции (машины) умножения;
Построить композиции МТ, реализующие вычисление функций, заданных с использованием операторов примитивной рекурсии и минимизации :
а)
б)
в)
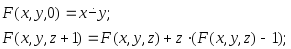
г)
д)
е)
ж)
з)
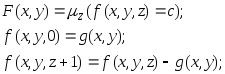
и)
