Тема 2. Рекурсивные функции
Рекурсивные функции представляют собой исторически первую формальную модель алгоритма. Они задают алгоритм как правило вычисления значения некоторой числовой функции. Ключевыми в данной теме являются понятия рекурсии и оператор примитивной рекурсии.
Рекурсия в самом общем виде – это есть правило определения ( или построения ) некоторого объекта с использованием его же самого.
Дадим некоторые важные определения.
Числовые функции, значения которых можно вычислять посредством единого для данной функции алгоритма, называются вычислимыми функциями. Вычислимая функция – интуитивное понятие, поскольку при ее определении использован термин « алгоритм ».
Арифметическими называются функции, области определения и значений которых – натуральный ряд.
Арифметические функции с ограниченной областью определения называются частными , остальные – всюду определенными.
Для первоначального ознакомления с рекурсивными функциями рекомендуется литература [ 1,4,8 ]. Для более полного изучения можно воспользоваться монографией А.И. Мальцева [ 5 ] или Р. Петер [ 6 ]. Книга [ 6 ] вместе с тем написана достаточно просто и понятно даже для неподготовленного читателя.
Задания на самостоятельную работу
Контрольные вопросы :
- что такое частичные функции, вычислимые функции ?
- перечислите простейшие функции, принятые в теории рекурсивных функций;
- что такое примитивно-рекурсивная функция ?
- как доказать примитивную рекурсивность функции ?
- являются ли примитивно-рекурсивные функции частичными или всюду определенными ? Почему ?
- что такое оператор минимизации? Когда он работает бесконечно?
- что такое общерекурсивная функция?
Задания
Показать, что функция f(n) - примитивно-рекурсивная. Привести тестовые примеры.
Сумма всех делителей n.
Количество взаимно простых с n чисел.
Количество нулей в двоичной записи n.
Сумма цифр в двоичной записи n .
Кол-во делителей числа n .
Максимальная цифра в 8-ричной записи n .
Минимальная цифра 8-ричной записи n .
Количество четных цифр в 8-ричной записи n .
Количество нечетных цифр в 8-ричной записи n .
Сумма простых делителей n .
Количество простых чисел, меньших либо равных n .
Количество чисел, меньших либо равных n, являющихся полными квадратами.
Сумма чисел, меньших либо равных n, являющихся степенью 2.
Максимальная цифра в 16-ричной записи n .
Минимальная цифра в 16-ричной записи n .
Ближайшее к n простое число.
Произведение простых делителей n .
Произведение взаимно простых с n чисел, меньших либо равных n .
Произведение нечетных делителей числа n, меньших либо равных n .
Произведение четных цифр 8-ричной записи числа.
MAX(НОД(n,m), HOK(n,m)).
Целая часть квадратного корня из n ,
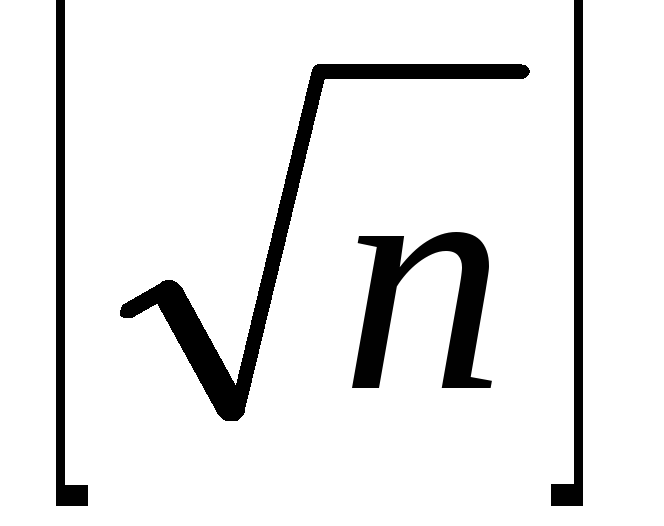.Целая часть корня степени y из x,
.Целая часть exp(x),
.
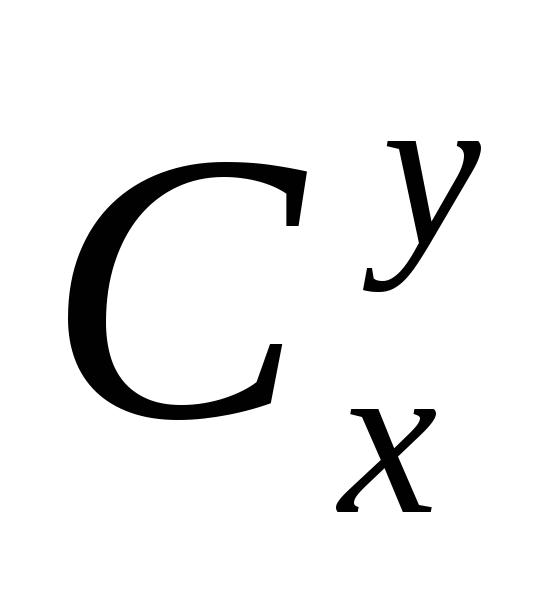(=1
при y>=x)Функция, перечисляющая по порядку числа Фибоначчи:
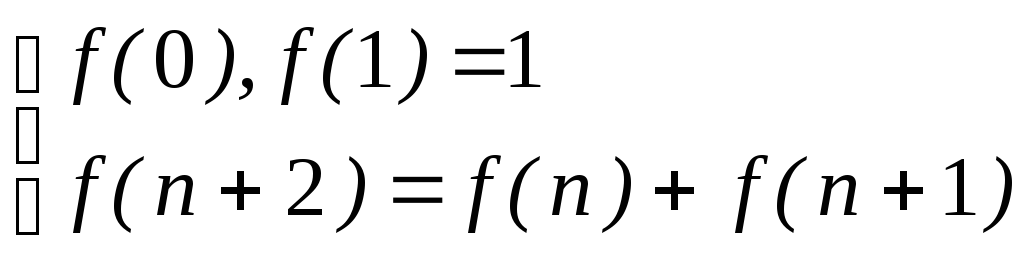
Задачи.
1.Доказать примитивную рекурсивность следующих функций и предикатов :
а)
б)
в)
г)
д)
е) « ступенька » :
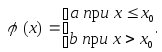
ж) функция, отличная от нуля в конечном числе точек;
з) (х) - сумма делителей числа x , где (0)=0
и) p(x) - произведение делителей числа х ;
к) (x) - количество делителей числа x ;
л) предикат : Х - четное число
м) предикат : Х делится на n ;
н)
- число простых чисел , не превосходящихx
:
о) K(x,y) - наименьшее общее кратное x и y , если K(x,0)=0 и K(0,y)=0;
п) d(x,y) - наибольший общий делитель чисел x и y , если d(0,0)=0;
р)
-
х-тое простое число
с)
,
где
т)
Используя операторы суперпозиции и примитивной рекурсии, докажите примитивную рекурсивность следующих функций :
а)
б)
в)
г)
(сумма по модулю 2);
д)
е) импликация xy ;
3.
Пусть функции
примитивно–рекурсивны. Доказать, что
тогда примитивно–рекурсивны и следующие
функции :
а)
б)
в)
г)
д)
если верхний предел суммирования меньше нижнего, то сумма равна нулю.
е)
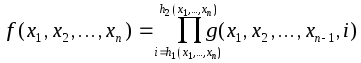
если верхний предел меньше нижнего, произведение равно 1.
Пусть
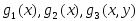примитивно–рекурсивные функции.
Докажите, примитивно–рекурсивна и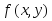
,
определяемая следующей схемой :
Приведите процесс вычисления функций по схеме примитивной рекурсии :
а)
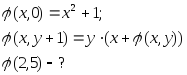
б)
в)
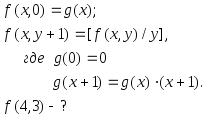
г)
д)
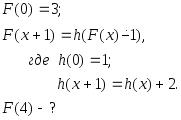
е)
ж)
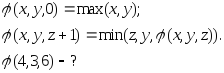
Докажите частичную рекурсивность следующих функций :
а)
б)
Применив операцию минимизации к подходящей примитивно–рекурсивной функции, докажите, что функция
является частично–рекурсивной :
а)
б)
в)
г)
д)
Приведите процесс вычисления функций с использованием оператора минимизации :
а)
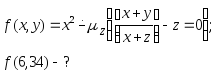
б)
в)
г)
