Для заметок к лекции № 3

Лекция № 4

Основы статистической обработки совокупности

случайных чисел

Вопросы, выносимые на лекцию: Понятие о случайной величине. Распределение вероятностей дискретной случайной величины. Закон распределения непрерывной случайной величины. Нормальное распределение непрерывных случайных величин. Распределение Стьюдента. Интегральная функция распределения.

4. ОСНОВЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ СОВОКУПНОСТИ

СЛУЧАЙНЫХ ВЕЛИЧИН

4.1 Понятие о случайной величине

Результат отдельно наблюдения при многократном прямом измерении какой-либо физической величины из-за наличия случайных погрешностей представляет собой случайную величину.

Поскольку закономерностей в появлении этих значений нет, анализ таких величин может производиться только методами теории вероятностей и математической статистики. Для характеристики случайной величины необходимо знать совокупность возможных значений этой величины, а также вероятности, с которыми эти значения могут появляться.

4.2 Распределение вероятностей значений дискретной случайной величины

Для дискретной случайной величинынаиболее полной статистической характеристикой является ее распределение вероятностей: указываются возможные значения этой величиныx_i и соответствующие им вероятностиp_i. Расположив значенияx₁, x₂, …, x_nв порядке возрастания и обозначив вероятностиp₁,p₂, …, p_n, получим график распределения вероятностей этой дискретной величины (рис. 4.1). Сумма всех вероятностей равна 1. Наиболее вероятной значение дискретной случайной величины называется модой (x^’на рис. 4.1).

Рис. 4.1

4.3 Закон распределения непрерывной случайной величины

Значения непрерывной случайной величины могут отличаться друг от друга сколь угодно мало, поэтому вероятность каждого из этих значений также бесконечно мала, и построить кривую распределения вероятностей невозможно.

Чтобы выявить распределение вероятностей в этом случае, рассматривается некоторое множество интерваловΔx_iв диапазоне возможных значений данной случайной величины, затем подсчитывают частотыn_i попадания значений в каждый из этих интервалов. Расположив, как и в предыдущем случае, значенияx_iв порядке возрастания и обозначив соответственно вероятностиp_i, получим ступенчатую кривую –гистограмму(рис. 4.2а). Соединив середины верхних отрезков гистограммы ломаной кривой, получимполигон частот (рис. 4.2б). Если взять бесконечно малые интервалы (Δx_i0), график потеряет ступенчатый характер и преобразуется в плавную кривую, называемуюкривой распределения плотности вероятностиf(x)для данной непрерывной случайной величины (рис. 4.2в). Уравнение, описывающее эту кривую, называется законом распределения данной непрерывной случайной величины. Площадь под всей кривойf(x) равна вероятности появления любого из возможных значенийx_i, т.е. равна 1:

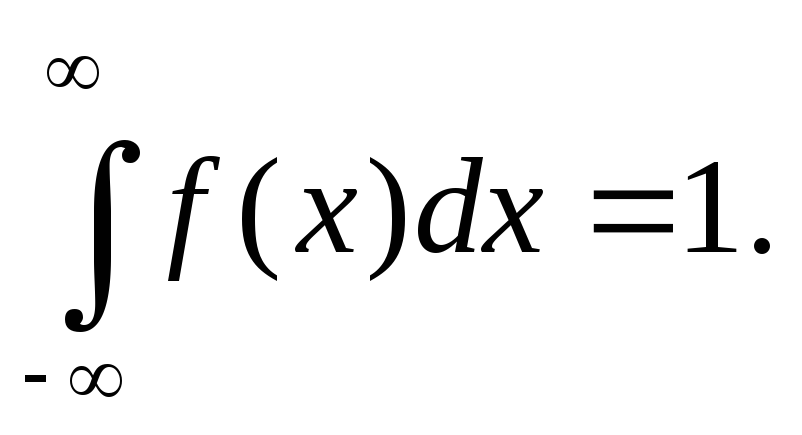
Модой для непрерывной случайной величины называется максимальное значение распределения.

Важным моментом является то, что существует оптимальное число интервалов группирования m, когда ступенчатая огибающая гистограммы наиболее близка к плавной кривой

Рис. 4.2

распределения генеральной совокупности. При слишком малом числе интервалов гистограмма будет отличаться от плавной кривой распределения вследствие слишком крупной ступенчатости (рис. 4.3а), из-за чего характерные особенности будут просто потеряны. Естественно считать, что появляющиеся при группировании провалы и выбросы являются случайным «шумом». Укрупнение интервалов группирования является методом фильтрации этого случайного «шума» (рис. 4.3б). Однако при слишком протяженных интервалах начнет «фильтроваться» уже не «шум», а сам «сигнал», т.е. начинают сглаживаться особенности искомого закона распределения.

Рис. 4.3

Оптимальное число интервалов можно рассчитать по формулам Старджеса

m = 3,3lg n + 1

Брукса и Каррузера

m = 5lg n

или Хайнольда и Гаеде

m =.

В области значений n<100результаты расчетов по вышеприведенным формулам близки между собой.