5.3 Методика обработки результатов прямых равноточных многократных измерений

Статистическая обработка экспериментальных выборок выполняется в такой последовательности:

• исключить (или уменьшить) систематические составляющие погрешности из результатов наблюдений одним из известных способов: введения поправок, замещения, компенсации, противопоставления;

• проверить соответствие экспериментального закона распределения теоретическому, нормальному (аналитическим или графоаналитическим способом). Для случая, когда можно предполагать, что данная выборка является частью генеральной совокупности, распределенной по нормальному закону, обработка продолжается;

• вычислить наиболее вероятное значение искомой величины как среднее арифметическое выборки

• вычислить среднеквадратичное отклонение sрезультата наблюдения по формуле

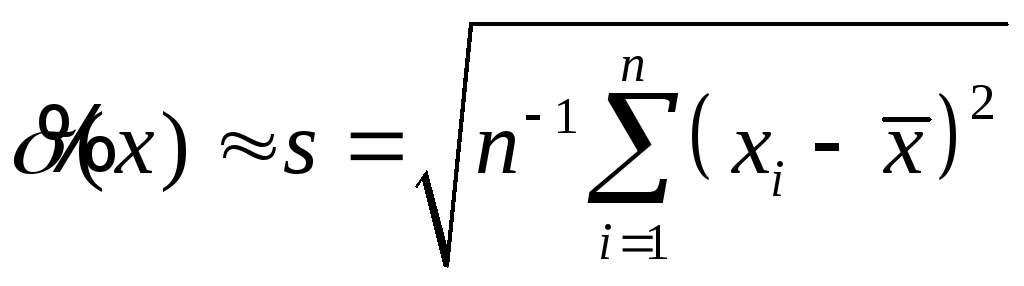
или формуле Бесселя

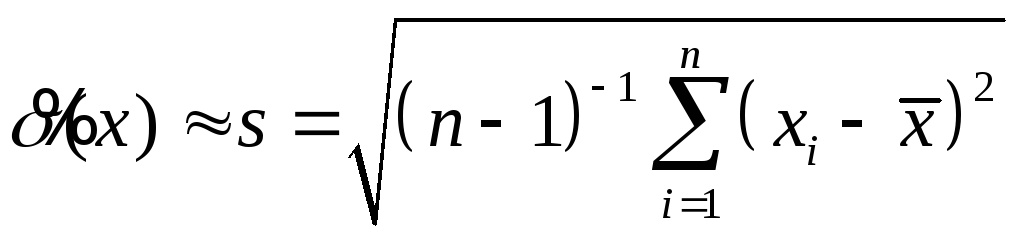
или формуле Петерса для упрощенного вычисления с.к.о.

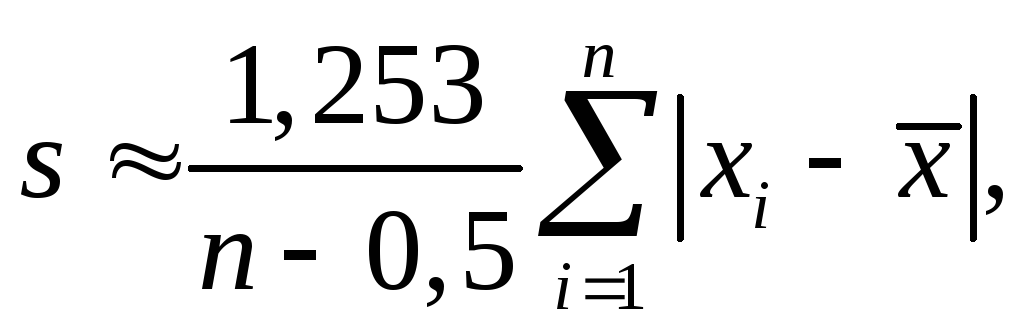
а для точных расчетов, учитывающих ограниченность числа опытов, по формуле

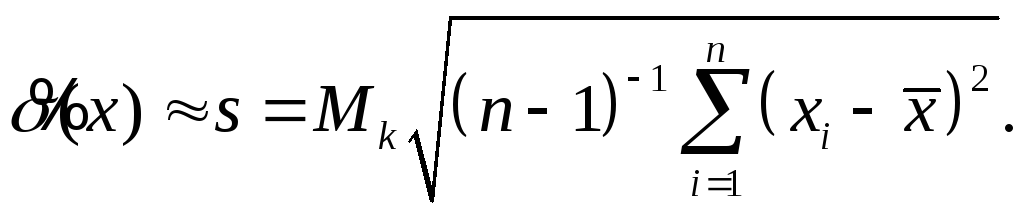
Значения коэффициента M_k приведены в литературе;

• при подозрении анормальности некоторого результата наблюдения x_k, который заметно отличается от остальных в выборке, вычислить показатель анормальности для этого результата

После этого сопоставить значение показателя V_kс табличной величинойβ для данного объема выборки и принятой вероятностиγ. Если подозрения подтвердятся (критерием анормальности является условиеV_k β), этот результат наблюдения должен быть из выборки исключен, а значенияиs вычислены заново (для этой же выборки, но безx_k);

• вычислить коэффициент вариации vдля данной выборки

v = 100 s/, %;

• вычислить среднеквадратичное отклонение результата измерения

• вычислить доверительные границы ε случайной составляющей погрешности общего результата измерения

x_н = - ε; x_в = + ε,

где ,

t_γ - коэффициент доверия, значения которого приведены в зависимости от числа степеней свободыk=n– 1 иγ/4/,

γ - двусторонняя доверительная вероятность.

Обычно для технических расчетов вычисление доверительных границ производится с доверительной вероятностью равной γ = 0,95, в отдельных случаях, когда эксперимент невозможно повторить, принимаютγ = 0,99 и только в особо ответственных случаях, когда результаты эксперимента влияют на жизнь и здоровье людей, допускается приниматьγ = 0,999;

• вычислить доверительные границы общей погрешности результата измерения. Если доверительные границы неисключенных остатков систематической составляющей погрешности результата измерения близка к нулю, можно принять

Δ A  ε;

• записать результат прямого измерения в виде

x = A ± Δ A; γ = 0,95,

где А– наиболее вероятное значение результата измерения (A  );

Δ A– доверительная граница погрешности измерения.

Полная форма записи обязательна в том случае, если γ  0,95.Приγ = 0,95значение вероятности в записи результата измерения часто опускают.

• Следует отметить, что существует следующие три основные правила округления рассчитанного значения погрешности и полученного экспериментального результата измерения:

• погрешность результата измерения указывается двумя значащими цифрами, если первая из них равна 1 или 2, и одной - если первая есть 3 и более;

• результат измерения округляется до того же десятичного разряда, которым оканчивается округленное значение абсолютной погрешности;

• округление производится лишь в окончательном ответе, а все предварительные вычисления проводят с одним-двумя лишними знаками.