6.2 Методика обработки результатов совокупных и совместных

измерений

Совокупные и совместные измерения позволяют определить искомые значения величинx₁, x₂, …, x_n,не поддающиеся непосредственному наблюдению, по результатам измерения значений других величинy₁, y₂, …, y_m,которые являются их функциями:

y_j = _j (x₁, x₂, …, x_n), (6.16)

где i = 1, 2, ..., n – порядковый номер неизвестных величинX,

j = 1, 2, ..., m – порядковый номер прямых измерений величинY.

После проведения прямых измерений значений величин Y_j результаты этих измерений подставляются в систему уравнений 6.16, решение которой позволяет найти искомые значения одноименных (присовокупных) или неодноименных (присовместных) величинx₁, x₂, …, x_n.

При совокупныхизмерениях непосредственно измеряют значения различных сочетаний одноименных величин, каждое из которых в отдельности измерить невозможно.

В совместныхизмерениях необходимо найти зависимость между несколькими неодноименными величинами.

Если в результатах прямых измерений величин Y_j содержатся случайные погрешности, то они имеются и в результатах совместных (совокупных) измерений величинX_i. Очевидно, что приm < nсистему 6.16 вообще решить невозможно; приm = nтакое решение алгебраически возможно, однако погрешности результатов измерений величинX_i будут, как и при прямых однократных измерениях, велики, и числовое значение этих погрешностей останется неизвестным. Приm > nсистема становится алгебраически неразрешимой, так как эти уравнения несовместимы, поскольку правые части уравнений 6.16 вместо точных значенийY_jсодержат результата их измеренийy_j = Y_j + Y_j со случайными погрешностямиY_j. Однако в последнем случае при нормальном законе распределения ошибок измерения величинy_j(что обычно и бывает) можно найти такую совокупность значенийx_i,которая с наибольшей вероятностью удовлетворяла бы исходным зависимостям 6.16. Это может быть осуществлено с помощью способа наименьших квадратов (принцип Лежандра).

Такой способ обработки экспериментальных данных при совокупных (совместных) измерениях особенно удобно применять при линейном характере функции _jв противном случае обработка усложняется.

Рассмотрим случай, когда функции _jлинейны:

(6.17)

Эту же систему запишем более компактно:

j=1, 2, …, m. (6.18)

Здесь индексы при коэффициентах aуказываются в последовательности «строка-столбец» (j – i).

Уравнения 6.17 и 6.18 называются условными. Ввиду наличия погрешностей правые части условных уравнений в действительности не будут равны нулю, а некоторым v_j (так называемым «невязкам», или остаточным погрешностям условных уравнений):

j=1, 2, …, m.(6.19)

В соответствии с принципом Лежандра наиболее вероятными значениями неизвестных величин X_iв этом случае будут такие, при которых сумма квадратов остаточных погрешностейv_j минимальна:

(6.20)

Необходимым условием такого минимума является равенство нулю производных

i=1, 2, …, n.(6.21)

Подставляя в выражение 6.21 значения v_jиз соотношения 6.19, получаем после преобразований систему нормальных уравнений:

h=1, 2, …, n.(6.22)

Запишем эту же систему в развернутом виде:

(6.23)

Здесь индексы при коэффициентах bтакже указывается в последовательности «строка-столбец» (h – i).

Поскольку число нормальных уравнений всегда равно числу неизвестных, такая система алгебраически разрешима.

Предположим, что в результате совместных (совокупных) измерений получена такая система условных уравнений:

при n = 2

(6.24)

при n = 3

(6.25)

Система нормальных уравнений имеет вид:

при n = 2

(6.26)

при n = 3

(6.27)

Коэффициенты b_hiможно вычислить по формулам:

(6.28)

Значения c_hопределяется следующим образом:

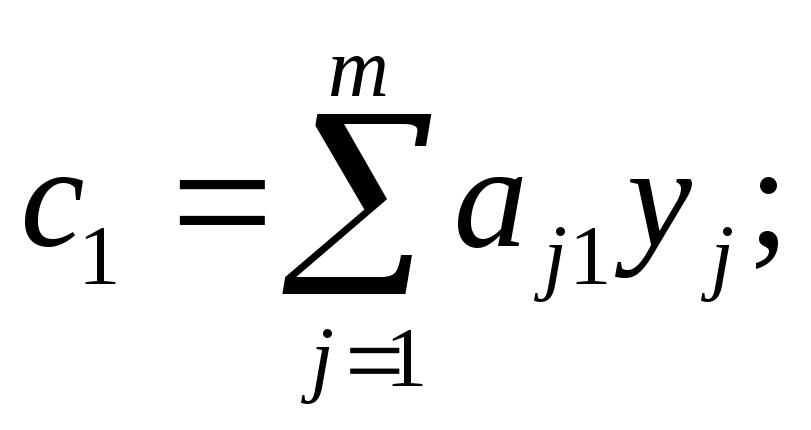
(6.29)

Для решения системы 6.23 составляем и вычисляем главный определитель данной системы уравнений:

для n = 2

(6.30)

для n = 3

(6.31)

Составляем и вычисляем частные определители D₁ иD₂, заменив в системе 6.23 коэффициентыb_hi при соответствующих неизвестных на свободные членыc_h:

для n = 2(6.32)

для n = 3 (6.33)

Вычисляем наиболее вероятные значения неизвестных:

для n = 2 (6.34)

для n = 3(6.35)

Подставив вычисленные наиболее вероятные значения неизвестных в условные уравнения 6.19, можно найтиv_j, затем получитьv_jи сумму квадратов остаточных погрешностей.

Среднеквадратичное отклонение результатов совокупных (совместных) измерений

(6.36)

где m– число условных уравнений;

n – число неизвестных;

A_hi – адъюнкты элементовb_hi главной диагонали определителяD (приh=i), полученные вычеркиванием строкиhи столбца i, соответствующих данному элементуb_hi, и последующим умножением на (-1)^h+i.

Для n = 2адъюнкты равны

(6.37)

для n = 3

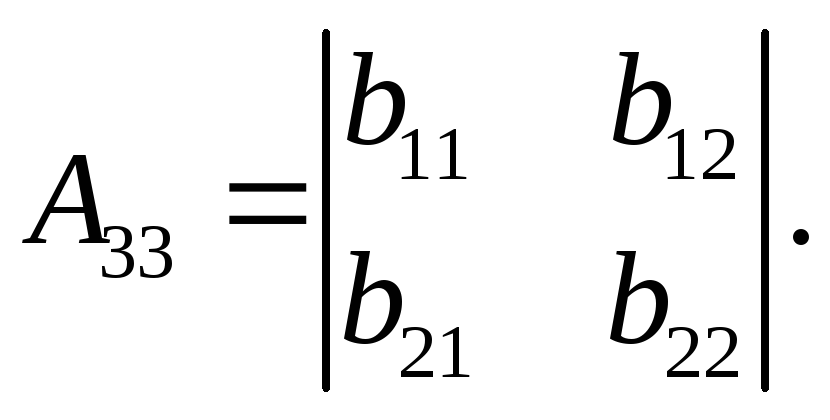(6.38)

Задавшись доверительной вероятностью , из приложения Б находим соответствующее значение коэффициента доверияt_γ. В этом случае число степеней свободы равно

k = m – n. (6.39)

Тогда можно найти доверительные границы случайной составляющей погрешности результата совокупных (совместных) измерений:

(6.40)

Вычисляем доверительные границы общей погрешности результата совокупного (совместного) измерения

.(6.41)

Записываем результат совокупного (совместного) измерения в виде

(6.42)

где – наиболее вероятное значениеi-го результата измерения ().

Контрольные вопросы.

1. Что такое косвенное измерение?

2. Как проверить корреляцию между результатами наблюдений каждой пары аргументов?

3. Как определить погрешность результата косвенного измерения?

4. Как определить доверительные границы случайной составляющей погрешности результата совокупных и совместных измерений?

Литература к лекции: [1], [2], [4]