5.4 Методика обработки результатов прямых неравноточных измерений

Неравноточные результаты измерений могут возникнуть в случаях, если физическая величина измерялась средствами измерений:

• различной точности;

• одинаковой точности, но при разном числе измерений;

• одинаковой точности и при одинаковом числе измерений, но в различных условиях.

Задача обработки неравноточных измерений состоит в определении достоверного значения измеряемой величины и оценке воспроизводимости измерений.

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Контрольные вопросы.

1. Как определить наиболее вероятное значение, среднеквадратичное отклонение результата наблюдения?

2. Как проверить подозрительный результат на промах?

3. Как вычислить доверительные границы случайной составляющей погрешности общего результата измерения?

Литература к лекции: [1], [2], [4]

Для заметок к лекции № 5

Лекция № 6

Обработка экспериментальных данных при косвенных,

совокупных и совместных измерениях

Вопросы, выносимые на лекцию: Методика обработки результатов косвенных измерений. Методика обработки результатов совокупных и совместных измерений

6.1 Методика обработки результатов косвенных измерений

Косвенные измерения– это измерения, результат которыхyопределяют на основании прямых измерений величинx₁, x₂, …, x_n, связанных с измеряемой величиной известной зависимостью. Уравнение косвенного измерения имеет вид:

y= f (x₁, x₂, …, x_n). (6.1)

Функциональная зависимость fназывается такжеформулой (уравнением) связи, а величиныx_i- измеряемыми аргументами.

Необходимость в косвенных измерениях возникает, если прямые измерения провести невозможно или слишком сложно, или если косвенные измерения дают более точный результат, чем прямые.

Исходными данными при косвенных измерениях являются ряды результатов наблюдений аргументов X_j,предварительно обработанные по методике, изложенной выше.

Методика обработки результатов косвенных измерений может использоваться только при условии постоянства аргументов и отсутствия взаимной связи между ними. Поэтому перед началом обработки, проанализировав попарно все результаты наблюдений аргументов, убедиться в отсутствии корреляции между ними. Если корреляционная связь не обнаружена, производится дальнейшая обработка: определяется результат косвенного измерения и оценивается его погрешность.

Погрешности косвенных измерений величины yзависят от погрешностей измерений величинx₁, x₂, …, x_n.

Если систематическими составляющими погрешностей прямых измерений аргументов можно пренебречь, а случайные погрешности измеряемых аргументов не зависят друг от друга, то обработка результатов косвенных измерений может осуществляться в следующей последовательности:

• производится проверка отсутствия корреляции между результатами наблюдений каждой пары аргументов, для чего вычисляется коэффициент корреляции Rмежду аргументамиX_h иX_lпо формуле:

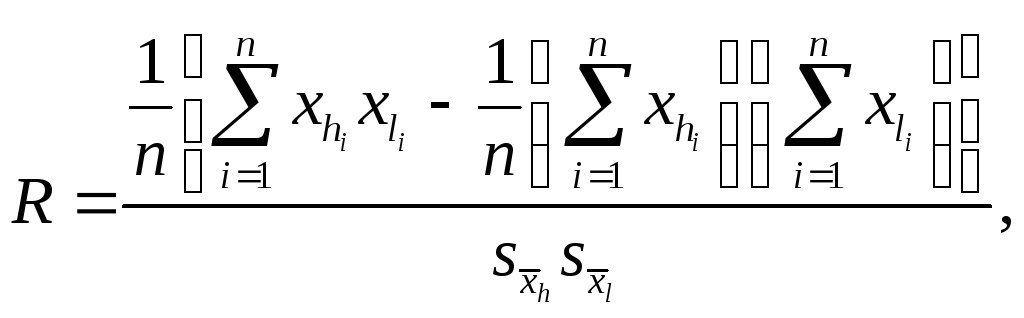(6.2)

где n– число наблюдений;ирезультатыi–го наблюдения соответственноh–го иl-го аргументов;

и- оценки среднеквадратичного отклонения результатов измерения этих аргументов.

Рассчитывается показатель корреляции

(6.3)

Критерием отсутствия корреляции является неравенство

K_R  t_,, (6.4)

где t_- коэффициент доверия при доверительной вероятности числе степеней свободыk = n – 1.

Если это неравенство удовлетворяется, то это значит, что корреляционная связь между данной парой аргументов X_h иX_l отсутствует. При наличии корреляционной зависимости между аргументами обработка экспериментальных данных при косвенных измерениях производится по более сложной методике и в настоящей работе не рассматривается;

• определяем наиболее вероятное значение измеряемой величины по выражению

(6.5)

где средние или средневзвешенные значения величинx₁, x₂, …, x_n;

• определяем погрешность результата косвенного измерения:

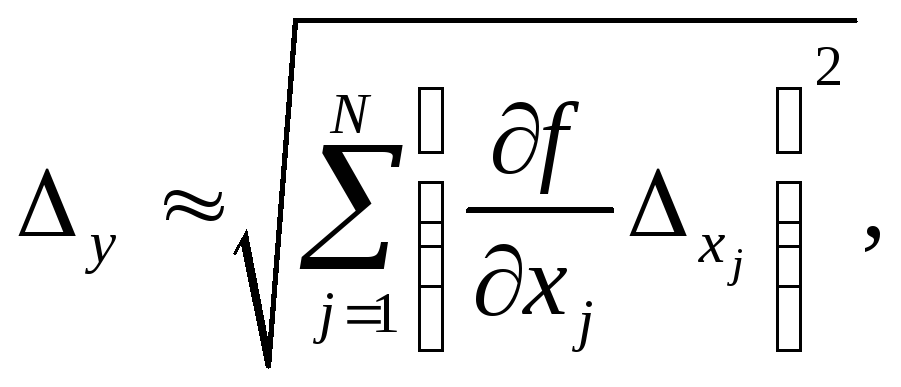(6.6)

где - частная погрешность результата косвенного измерения;

- частная производная отy из уравнения связи поj-му измеряемому аргументу;

- абсолютная погрешность прямого измеренияj-го аргумента.

Для алгебраической суммы

Y = a*X₁ + b*X₂ + … (6.7)

абсолютная погрешность результата

(6.8)

Для произведения

(6.9)

погрешность результата

(6.10)

определяем среднеквадратичную погрешность результата косвенного измерения

(6.11)

где - среднеквадратичные погрешности результатов прямых измерений аргументовx_j ;

• вычисляем доверительные границы случайной составляющей погрешности результата косвенного измерения

(6.12)

где γ - доверительная вероятность,

t_γ - коэффициент доверия, значения которого рассчитывается следующим образом.

Сначала вычисляется эффективное число степеней свободы для данного косвенного измерения:

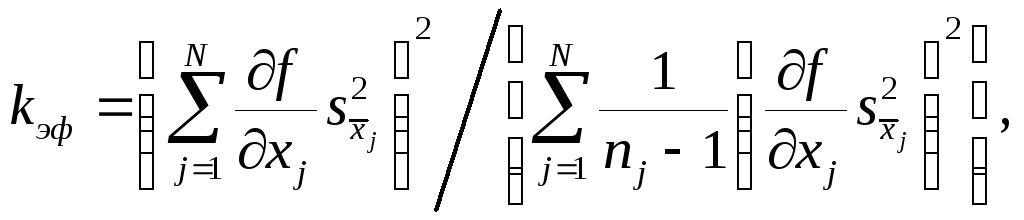(6.13)

где n_j - число прямых измерений аргументаx_j .

Если все n_jодинаковы и равныn, то

Задавшись значением γ, находим дляk = k_эф (если значениеk_эф получилось дробным, его следует округлить) величину t_γ;

• вычисляем доверительные границы общей погрешности результата косвенного измерения

Δ A_y  ε; . (6.14)

записываем результат косвенного измерения в виде

y = A ± Δ A; γ = 0,95, (6.15)

где А– наиболее вероятное значение результата измерения (A  ).