
- •Министерство образования , науки, молодежи и спорта
- •Содержание
- •Раздел 1. Термические параметры состояния 6
- •Лекция №1
- •Введение
- •Раздел 1
- •1. Термические параметры состояния
- •1.1 Давление
- •1.2 Температура.
- •1. 3 Связь между параметрами состояния
- •1.4 Калорические параметры состояния. Внутренняя энергия
- •1.4 Параметры процесса Работа и теплота
- •Контрольные вопросы
- •2.2 Первый закон термодинамики для закрытой системы
- •Лекция № 3
- •Раздел 3
- •3. Основные термодинамические процессы идеального газа
- •3. 1 Законы идеального газа
- •3.2 Изохорный процесс
- •3.4 Изобарный процесс
- •3.5 Изотермический процесс
- •3.6 Адиабатный процесс
- •3.7 Политропные процессы и их обобщающие значения
- •Контрольные вопросы.
- •Лекція № 4
- •4. Второе начало термодинамики
- •4.1 Общие понятия
- •4.2 Круговые процессы ( циклы) тепловых машин
- •Цикл Отто
- •Цикл Дизеля
- •4.3 Устройство четырехтактного двигателя.
- •4. 4. Двухтактные двигатели.
- •4.5. Индикаторная мощность
- •4.6. Наддув.
- •4.7. Тепловой баланс и показатели экономичности двс.
- •4.8. Основные конструктивные элементы двс.
- •4.9. Термодинамический цикл газотурбинной установки (гту) с изобарным подводом теплоты
- •Контрольные вопросы.
- •Раздел 5
- •5. Общие свойства жидкостей и паров
- •5.1 Основные параметры состояния жидкости и пара
- •Теплота парообразования.
- •5.2 Диаграмма состояния воды и водяного пара I-s
- •Лекция № 6
- •Раздел 6
- •6. Влажный воздух
- •Лекция № 7
- •Раздел 7
- •7. Основы теплообмена
- •7.1. Общие понятия.
- •8.2. Перенос теплоты теплопроводностью через плоскую стенку.
- •Лекция № 8
- •Раздел 8
- •8. Конвективный теплообмен.
- •8.1 Подобие процессов конвективного теплообмена. Числа подобия.
- •Контрольные вопросы.
- •1. Закон Планка. Интенсивность излучения абсолютно черного тела js,λ и любого реального тела Jλ зависит от температуры т и длины волны λ.
- •3. Закон Стефана (1879 г.) – Больцмана (1884 г.).
- •9.2. Теплообмен между твердыми телами
- •При установке экрана
- •Контрольные вопросы.
- •Учебно-методические материалы
- •Конспект лекций Теоретические основы теплотехники
3.2 Изохорный процесс
В общем виде основное уравнение изохорного процесса
p = f1(v=const; T). Рассматривая уравнение Клапейрона (3.2) для идеального газа в состоянии 1 и 2 , и учитывая уравнение изохоры v1=v2 =const, получим соотношение параметров для изохорного процесса:
1. p2 /p2 =T2 /T1. ( 3.4). 2. Поскольку объём постоянен, т.е. dv =0, то работа изменения объёма равна нулю
(l1-2=![]() ).
Удельная техническая работа lTEX
= -
v(p2
– p1)
(пл.1-2, p1/p2
рис3.2 )
Из общего уравнения первого закона
термодинамики (разд. 2). количество
теплоты, подведенное в изохорный
процесс, полностью затрачивается на
изменение внутренней энергии, т.е. при
dv
= 0 δq
= du
qV1-2
=u2
(v2T2
) – u1(
v1T1)
отсюда
).
Удельная техническая работа lTEX
= -
v(p2
– p1)
(пл.1-2, p1/p2
рис3.2 )
Из общего уравнения первого закона
термодинамики (разд. 2). количество
теплоты, подведенное в изохорный
процесс, полностью затрачивается на
изменение внутренней энергии, т.е. при
dv
= 0 δq
= du
qV1-2
=u2
(v2T2
) – u1(
v1T1)
отсюда
u2
(v2T2
) – u1(
v1T1)
=
 (3.5).
(3.5).
поэтому dq = Cvd T, qV1-2 = cV (T2 – T1).
3. Изменение энтропии в процессе определим из соотношения ds = dq/T = CV dT; интегрируя его, получим
s2 – s1= CVln (T2/T1 ) (3.6).
На T-S диаграмме линия V = const изображается логарифмической кривой процесса ( рис. 3.2 ).
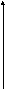


 Р
Т
2
Р
Т
2
Р

 2
1
1
qV1-2
2
1
1
qV1-2
l ТЕХ


 Р1
2
Р1
2
0 V 0 S1 S2 S
Рисунок 3.2. График изохорного процесса
Пример 3.1. В баллоне емкостью 15 л содержится воздух при давлении 0,4 МПа и температуре 300 С. Какова будет температура воздуха в результате подвода к нему
16 кДж теплоты ? Удельная изохорная теплоемкость Cvm = 717 Дж/(кг.К); газовая постоянная R = 287,1 Дж/(кгК).
Р е ш е н и е . 1. Предварительно вычислим массу воздуха m по формуле (3.3)
m = p1 V/ (RT1 ) = 0,4*106 *0,015/(287,1*303)=0,069 кг.
2. Найдем конечную температуру t2 из уравнения (3.5)
Q1,2 = mcvm (t2 – t1 ) откуда
t2
= t1
+
![]()
3.4 Изобарный процесс
Общее уравнение изобарного процесса v = f(T, p =const).
1. Из равенства P1 ·V1 = RT1 и P2·V2 = RT2 получим
![]() ,
удельный объем v
возрастает при подведении теплоты и
уменьшается при охлаждении рабочего
тела.
,
удельный объем v
возрастает при подведении теплоты и
уменьшается при охлаждении рабочего
тела.
2. Удельная работа в процессе ( на P – V диаграмме пл. 1,2v2 v1)
l1-2
= p(v2
- v1)
= R(
T2
– T1),
(3.9).
техническая
работа ℓTEX
= -
![]() = 0
= 0
p


 1
lP1-2
2 dℓ = pdv;
ℓ=
1
lP1-2
2 dℓ = pdv;
ℓ=
![]() =p(
v2
– v1)
=p(
v2
– v1)

0 V1 V2 V
Удельное количество теплоты определяем из первого закона т/динамики:δq = dh. Количество теплоты в изобарном процессе равно изменению энтальпии
рабочего тела qp2-1 = h2 –h1 ( на T-S диаграмме пл. 12S2S1).
T

 V
=const 1
V
=const 1
 Т2
2
Т2
2

 Т1
P = const
Т1
P = const

 S
S
0 S1 S2
3.Изменение внутренней энергии равно
Δu = CV ( T2 – T1) ; CV ≠ f (T)
4. Изменение энтальпии Δh = CP (T2 – T1); CP ≠ f (T)
5. Изменение энтропии в изобарном процессе
s2(p;T2)
- S1(p;
T1)
=
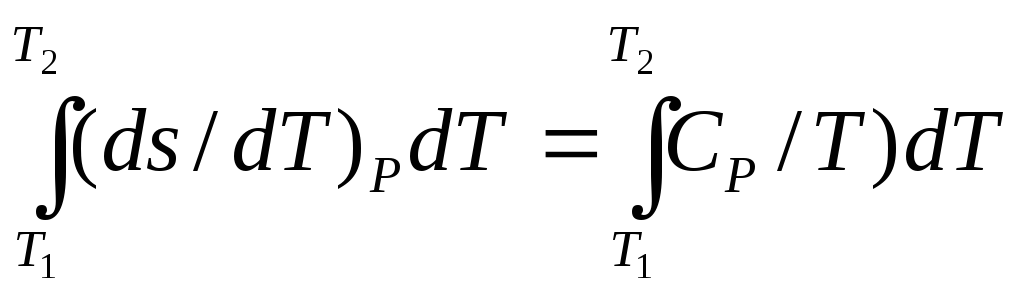 (3.8).
(3.8).
Если в интервале Т1……Т2 теплоемкость СР постоянна, то
S2 – S1 = CР· ln( T2 – T1)
Изобара на Т-S диаграмме изображается логарифмической кривой. Если СP>CV , то при одинаковом изменении температуры ΔSP>S V , следовательно, на Т-S диаграмме изобара располагается более полого, чем изотерма.
Пример 3.2. Азот массой 0,5 кг расширяется по изобаре при абсолютном давлении 0,3 МПа так, что его температура повышается от 100 до 3000С.
Найти конечный объём азота, совершенную работу и подведенную теплоту. Удельная газовая постоянная R = 296,8 Дж/(кг.К).
Р е ш е н и е. 1. Находим начальный объем азота из уравнения (3.5):
V1 = mRT1/p1 =0,5*296,8*373/(0,3*106) = 0,184 м3
2. Теперь найдем конечный объем:
V2 = V1*T1/T2 =0,184*573/373 = 0,284 м3.
3. Определим работу изменения объёма (уравнение 3.7)
L1,2=p (V2 – V1) = 0,3*106 (0.287- 0.184)= 30*103 Дж
4. Работа изменения давления l ТЕХ = 0.
5. Определим теплоту, подведенную к газу по уравнению
Q1,2 = mcpm(t2 – t1), заменяя Т2-Т1 на t2 -t1
При средней температуре tm (t1 + t2)/2 = 200ОС
средняя удельная изобарная теплоемкость азота равна
Cpm = Cpm/M=29, 38*103/28,02 = 1047 Дж/(кгК)
Таким образом,
Q1,2=0,5*1047(300-100)=104,7*103 Дж.
