17. Степенные ряды.

Ряд вида называетсястепенным рядом. Числа ,,, …,, … называются коэффициентами степенного ряда.

Придавая различные числовые значения, будем получать различные числовые ряды, которые могут оказаться сходящимися или расходящимися. Множество тех значений, при которых рядсходится, называется областью его сходимости.

Структура области сходимости степенного ряда устанавливается с помощью теоремы Абеля.

Теорема. Если степенной ряд сходиться при значении, то он сходиться и, притом абсолютно при всех значенияхтаких, что.

Следствие. Если степенной ряд расходиться при значении, то он расходиться при всех значенияхтаких, что.

Из теоремы Абеля следует, что если есть точка сходимости ряда, то интервалвесь состоит из точек сходимости данного ряда, при всех значенияхвне этого интервала рядрасходиться.

	ряд сходиться
ряд расходиться		ряд расходиться

Интервал называют интервалом сходимости степенного рада. Положивинтервал сходимости можно записать в виде. Числоназывают радиусом сходимости степенного ряда, т.е.– это такое число, что при всех, для которыхрядабсолютно сходиться, а приряд расходиться.

Отметим, что на концах интервала сходимости (т.е. при и при) сходимость ряда проверятся в каждом случае отдельно.

Рассмотрим степенной ряд . Радиус сходимости данного ряда можно определить по формуле. Отметим, что если рядсходится на всей числовой прямой, то, если ряд сходится только при, то.

Пример 17.1. Найти область сходимости степенного ряда .

Решение. Так как ,, то радиус сходимости равен. Интервал сходимости ряда. Исследуем поведение ряда на концах интервала сходимости.

При данный степенной ряд принимает вид. Исследуем знакочередующийся ряд по признаку Лейбница. Так как элементы знакочередующегося ряда убывают по абсолютной величине, и предел общего элемента, следовательно, ряд сходится.

При данный степенной ряд принимает вид. Сравним данный ряд с гармоническим рядом, у которого. Так как, то исследуемый ряд расходится, так как расходится ряд.

Итак, область сходимости ряда .

Рассмотрим ряд . Радиус сходимости ряда, заданного по степеням, находиться по формуле, интервал сходимости определяется из условияили.

Пример 17.2. Найти радиус и интервал сходимости степенного ряда .

Решение. Радиус сходимости степенного ряда равен. Интервал сходимости ряда естьили. Выясним поведение ряда на концах интервала сходимости.

При данный степенной ряд принимает вид. Исследуем знакочередующийся ряд по признаку Лейбница. Элементы знакочередующегося ряда убывают по абсолютной величине, и предел общего элемента, следовательно, ряд сходится.

При данный степенной ряд принимает вид. Рядявляется обобщенным гармоническим рядом, следовательно, он сходится

Итак, область сходимости ряда .

18. Ряд Маклорена.

Приведем таблицу, содержащую разложения в ряд Маклорена некоторых элементарных функций:

, ,

, ,

, ,

, ,

,

.

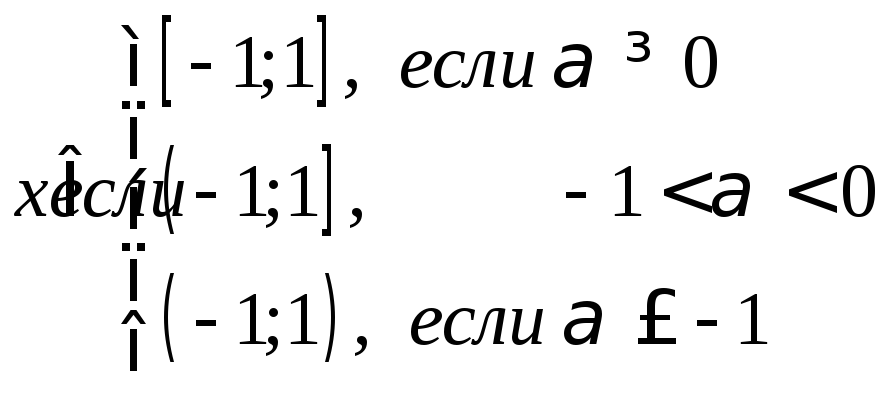Пример 18.1. Разложить в ряд Маклорена функцию .

Решение. Так как , то заменяяна, получим

. Область сходимости ряда .