
- •Санкт-петербургский университет
- •17. Степенные ряды.
- •18. Ряд Маклорена.
- •19. Дифференциальные уравнения первого порядка.
- •20. Дифференциальные уравнения второго порядка.
- •Рекомендации по решению типовых задач по контрольной работе № 5
- •21. Определение вероятности.
- •22. Теорема сложения и умножения вероятностей.
- •23. Формула полной вероятности и Байеса.
- •24. Случайные величины.
- •25. Нормальное распределение.
- •Рекомендации по решению типовых задач по контрольной работе № 6
- •26. Выборочный метод. Статистические оценки параметров распределения.
- •27. Интервальные оценки
- •28. Корреляционный анализ.
- •29. Регрессионный анализ.
- •30. Проверка статистических гипотез.
- •Рекомендуемая литература
Санкт-петербургский университет
ГОСУДАРСТВЕННОЙ ПРОТИВОПОЖАРНОЙ СЛУЖБЫ МЧС РОССИИ

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ
ПО ВЫСШЕЙ МАТЕМАТИКЕ
для слушателей заочного обучения
направление подготовки 280705.65 – Пожарная безопасность
квалификация (степень) – специалист
Санкт-Петербург
2012
Санкт-Петербургский университет
государственной противопожарной службы МЧС России
Калинина Е.С., Крюкова М.С., Медведева О.М.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ
ПО ВЫСШЕЙ МАТЕМАТИКЕ
для слушателей заочного обучения
направление подготовки 280705.65 – Пожарная безопасность
квалификация (степень) – специалист
Санкт-Петербург
2012
СОДЕРЖАНИЕ
4
Рекомендации по решению типовых задач по контрольной работе № 4 4
Рекомендации по решению типовых задач по контрольной работе № 5 16
Рекомендации по решению типовых задач по контрольной работе № 6 25
Рекомендуемая литература 37
Рекомендации по решению типовых задач по контрольной работе № 4
16. Числовые ряды
Числовым
рядом
называется бесконечная последовательность
чисел
![]() ,
,![]() ,
…,
,
…,![]() ,
… соединенных знаком сложения:
,
… соединенных знаком сложения:![]() .
Числа
.
Числа![]() ,
,![]() ,
…,
,
…,![]() ,
… называются элементами ряда, а элемент
,
… называются элементами ряда, а элемент![]() – общим или
– общим или![]() элементом ряда.
элементом ряда.
Рассмотрим
суммы конечного числа элементов ряда:
![]() ,
,![]() ,
,![]() ,
…,
,
…,![]() .
Сумма
.
Сумма![]() первых элементов ряда называется
первых элементов ряда называется![]() частичной суммой ряда.
частичной суммой ряда.
Ряд
называется сходящимся,
если существует конечный предел
последовательности его частичных сумм,
т.е.
![]() .
.
Число
![]() называется суммой ряда, тогда можно
записать
называется суммой ряда, тогда можно
записать![]() .
Если конечного предела последовательности
частичных сумм не существует, то ряд
называетсярасходящимся.
.
Если конечного предела последовательности
частичных сумм не существует, то ряд
называетсярасходящимся.
Пример
16.1. Исследовать
ряд
![]() на сходимость.
на сходимость.
Решение.
Сумма
![]() первых элементов ряда
первых элементов ряда![]() равна
равна![]() .
.
Найдем
предел последовательности частичных
сумм
![]() .
Так как предел последовательности
частичных сумм существует, то по
определению о сходимости ряда исследуемый
ряд сходится.
.
Так как предел последовательности
частичных сумм существует, то по
определению о сходимости ряда исследуемый
ряд сходится.
Установить
сходимость (расходимость) ряда путем
определения
![]() частичной суммы и вычисления предела
последовательности частичных сумм
возможно далеко не всегда из-за
принципиальных трудностей при нахождении
частичной суммы и вычисления предела
последовательности частичных сумм
возможно далеко не всегда из-за
принципиальных трудностей при нахождении![]() .
Проще это можно сделать на основании
признаков сходимости.
.
Проще это можно сделать на основании
признаков сходимости.
Теорема
(необходимый признак сходимости).
Если ряд ![]() сходится, то предел
его общего элемента
сходится, то предел
его общего элемента
![]() при
при![]() равен нулю, т.е.
равен нулю, т.е.![]() .
.
Следствие.
Если предел общего элемента
![]() ряда
ряда![]() при
при
![]() не равен нулю, т.е.
не равен нулю, т.е.![]() ,
то ряд расходится.
,
то ряд расходится.
Пример
16.2. Исследовать
сходимость ряда
![]() .
.
Решение.
Общий элемент ряда равен
![]() .
Найдем предел общего элемента ряда:
.
Найдем предел общего элемента ряда: .
Необходимый признак сходимости не
выполняется, следовательно, ряд
расходится.
.
Необходимый признак сходимости не
выполняется, следовательно, ряд
расходится.
Необходимый признак сходимости не дает возможности судить о том, сходиться ли данный ряд или нет. Сходимость и расходимость ряда во многих случаях можно установить с помощью достаточных признаков.
Рассмотрим некоторые из них для знакоположительных рядов, т.е. рядов с неотрицательными членами.
Теорема
(Признак Даламбера).
Если для ряда с положительными элементами
![]() существует предел отношения
существует предел отношения![]() элемента к
элемента к![]() элементу
элементу![]() ,
то при
,
то при![]() ряд сходится, при
ряд сходится, при![]() ряд расходится, при
ряд расходится, при![]() вопрос о сходимости ряда остается
нерешенным.
вопрос о сходимости ряда остается
нерешенным.
Пример
16.3. Исследовать
сходимость ряда
![]() .
.
Решение.
Так как
![]() ,
,![]() ,
то
,
то![]()
![]() .
Предел отношения
.
Предел отношения![]() элемента к
элемента к![]() элементу равен
элементу равен![]() ,
следовательно, ряд сходится по признаку
Даламбера.
,
следовательно, ряд сходится по признаку
Даламбера.
Теорема
(Признак Коши).
Если для ряда с положительными элементами
![]() существует предел
существует предел![]() ,
то при
,
то при![]() ряд сходится, при
ряд сходится, при![]() ряд расходится, при
ряд расходится, при![]() вопрос о сходимости ряда остается
нерешенным.
вопрос о сходимости ряда остается
нерешенным.
Пример
16.4. Исследовать
сходимость ряда
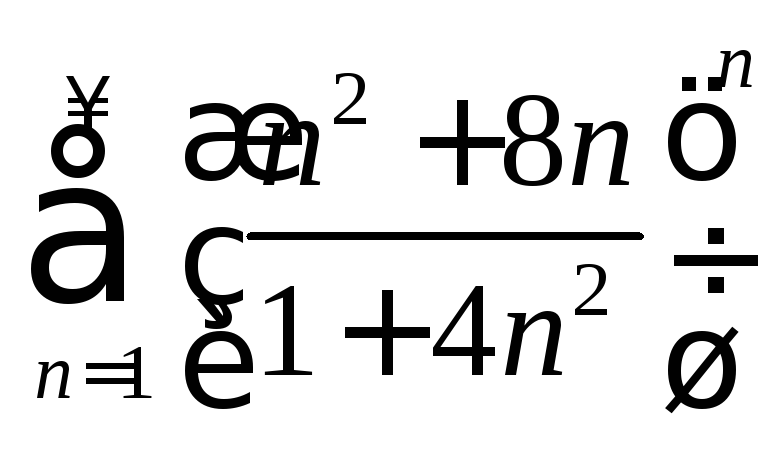 .
.
Решение.
Исследуем данный ряд по признаку Коши.
Так как
![]() ,
то исследуемый ряд сходится.
,
то исследуемый ряд сходится.
Теорема
(предельный признак сравнения).
Если для рядов
![]() и
и![]() с положительными элементами существует
конечный предел отношения их общих
элементов
с положительными элементами существует
конечный предел отношения их общих
элементов![]() ,
то ряды одновременно сходятся, либо
расходятся.
,
то ряды одновременно сходятся, либо
расходятся.
Признак сравнения дает возможность установить сходимость или расходимость некоторых числовых рядов путем сравнениях их с другими рядами, сходимость или расходимость которых известна заранее. Как правило, в качестве эталонов при применении данного признака используются следующие ряды:
1. геометрический
ряд
![]() – сходится при
– сходится при![]() ,
расходиться при
,
расходиться при![]() ;
;
2. гармонический
ряд
![]() – расходится;
– расходится;
3. обобщенный
гармонический ряд
![]() – сходится при
– сходится при![]() ,
расходится при
,
расходится при![]() .
.
Пример
16.5. Исследовать
сходимость ряда
![]() .
.
Решение.
Сравним ряд с обобщенно гармоническим
рядом
![]() ,
у которого
,
у которого![]() .
Так как
.
Так как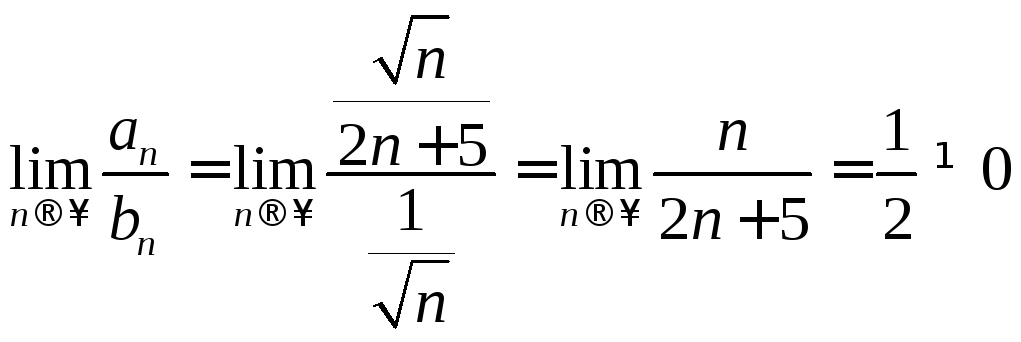 ,
то исследуемый ряд расходится, так как
расходится ряд
,
то исследуемый ряд расходится, так как
расходится ряд![]() .
.
Рассмотрим
важный класс рядов, называемых
знакочередующимися. Знакочередующимся
рядом
называется ряд вида
![]()
![]() ,
где
,
где![]() для всех
для всех![]() .
.
Для исследования сходимости знакочередующихся рядов применяется признак Лейбница.
Теорема
(признак Лейбница).
Если элементы знакочередующегося ряда
убывают по абсолютной величине
![]() и предел его общего элемента при
и предел его общего элемента при![]() равен нулю, т.е.
равен нулю, т.е.![]() ,
то ряд сходится, а его сумма не превосходит
первого элемента:
,
то ряд сходится, а его сумма не превосходит
первого элемента:![]() .
.
Пример
16.6. Исследовать
сходимость ряда
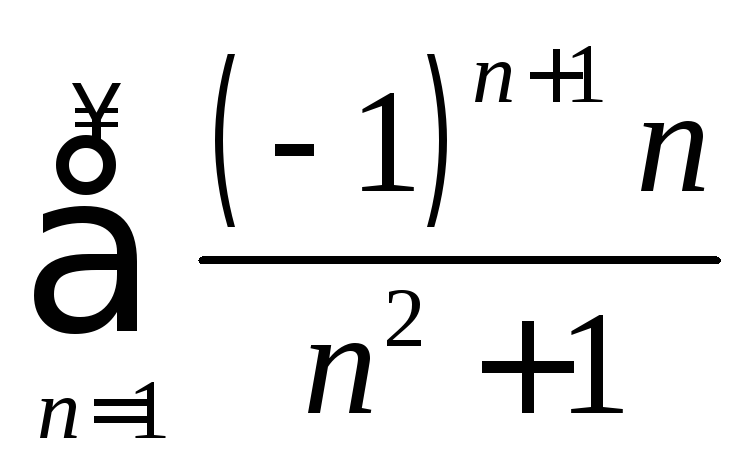 .
.
Решение.
Так как элементы знакочередующегося
ряда убывают по абсолютной величине
![]() ,
и предел общего элемента равен
,
и предел общего элемента равен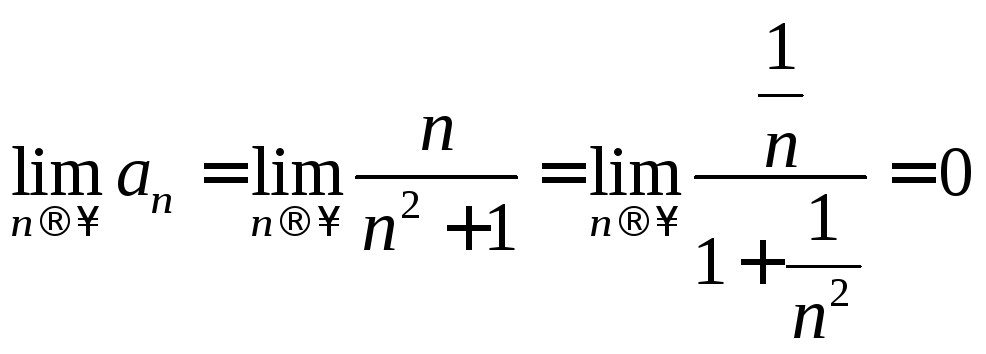 ,
то по признаку Лейбница ряд сходится.
,
то по признаку Лейбница ряд сходится.
