Расчет коллекторов круглого сечения

При герметизированном нижнем сливе коллектор укладывается параллельно железнодорожному пути на расстоянии не менее 1,8 м от оси пути. При самотечном сливе эти коллекторы представляют собой безнапорные трубопроводы круглого сечения. Расход нефтепродуктов в таких коллекторах определяется по формуле

(2.48)

где φ — угол, характеризующий степень заполнения трубы (рис. 2.10, а).

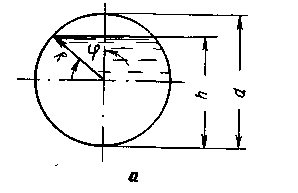
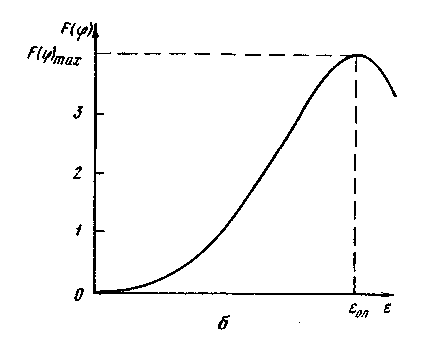
Рис. 2.10. К расчету безнапорного коллектора круглого сечения (а) и характеристика безнапорного трубопровода (б)

Функция f (φ) определяет влияние степени заполнения трубы на расход и вычисляется методом численного интегрирования. В табл. 2.2 приведены значения f (φ) в зависимости от φ и степени заполнения ε = h/d. Здесь же даны значения отношений расходов при неполном заполнении Qφ к расходам при полном заполнении сечения трубы (Q₀).

Таблица 2.2

Значения f (φ) в зависимости от степени заполнения нефтепровода

φ	ε=	f (φ)
0 7,5 15 30 45 60 75 90 120 150	1,000 0,996 0,988 0,932 0,853 0,751 0,629 0,500 0,250 0,067	3,1416 3,1973 3,3741 3,7994 4,0197 3,6268 2,6790 1,5708 0,3348 0,0025	1,000 1,018 1,074 1,209 1,279 1,155 0,853 0,500 0,106 0,001

Из приведенной табл. 2.2 и графика на рис. 2.10, б видно, что расход в безнапорном трубопроводе при малых степенях заполнения больше, чем при полном заполнении трубы, и достигает максимального значения Q_φ = 1,279Q_о при φ = 45°. Это явление объясняется тем, что с уменьшением степени заполнения от 1 до 0,7 гидравлический радиус незаполненного трубопровода больше, чем заполненного, и достигает максимума при ε = 0,853. Затем по мере дальнейшего уменьшения е наблюдается обратное явление, когда гидравлический радиус незаполненного трубопровода становится меньше по сравнению с заполненным трубопроводом.

При турбулентном режиме движения расход в коллекторе можно определять по формуле

(2.49)

Для определения размеров поперечного сечения сливных трубопроводов необходимо знать величину расчетного расхода. При сливе одной цистерны: этот расход определяется, как

Расход для коллекторов рассчитывается для нескольких цистерн или целого маршрута. При этом Q_р определяют с учетом неодновременности начала слива из различных цистерн. Время запаздывания Δτ складывается из времени, затрачиваемого на подготовительные операции. Расход в коллекторе равен сумме расходов из каждой цистерны маршрута. Расход из первой цистерны, откуда только что начался слив,

Если из второй цистерны слив начался раньше на Δτ, то часть нефтепродукта из нее уже сольется и истечение будет происходить при уровне h₂<D, а следовательно, и q₂ < q₁ (рис. 2.11).

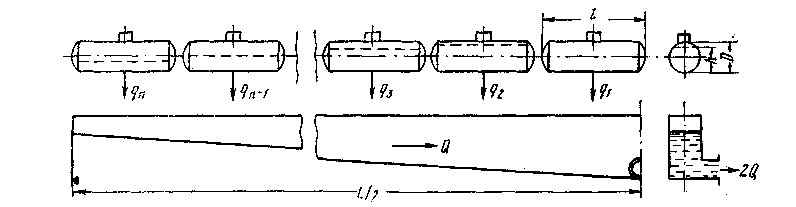
Рис. 2.11. К определению расчетного расхода сливного коллектора.

Уровень нефтепродукта определится из формулы (2.31):

Отсюда

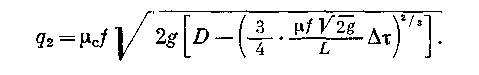
Расход из третьей цистерны, сливающейся в течение 2 Δτ времени, будет еще меньше и по аналогии со второй цистерной составит:

Если число цистерн в маршруте N, а бригада сливщиков одновременно может обработать а цистерн, тогда расход из п-й цистерны с учетом поправок на запаздывание составит:

При сливе на одной половине коллектора 0,5 маршрута расчетный расход составит:

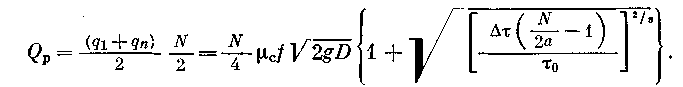(2.49)

Таким образом, гидравлический расчет коллекторов сводится к нахождению размеров поперечного сечения при известном расходе Q_p и заданном уклоне i. Обычно величину i принимают в пределах от 0,005 до 0,01.

Слив по схеме (см. схему на рис. 1.12, г) производится через специальный трубопровод при помощи насосов. Если применяется самовсасывающий насос, способный создать разрежение в трубопроводе =h_вс, то расчет такой системы сводится к проверке неравенства

(2.50)

где Δz — разность отметок начала и конца нефтепровода.

В случае применения несамовсасывающих насосов неравенство (2.50) запишется в виде

Отводная труба при подключении к середине сливного коллектора рассчитывается по удвоенному расходу в коллекторе. При движении нефтепродукта в отводной трубе полным сечением диаметр ее определяется по формуле

(2.51)

где Δz — разность отметок нижнего уровня нефтепродукта в коллекторе и оси отводной трубы у нулевого резервуара.

Если движение потока в отводной трубе происходит неполным сечением, то d определяют по формуле (2.48).

При сливе высоковязких нефтепродуктов из цистерн, оборудованных паровой рубашкой, в отводную трубу поступает поток в вязко-пластическом состоянии. Чтобы это звено сливной коммуникации не лимитировало производительность слива, необходимо предусмотреть внешний обогрев трубы.

Движение таких потоков мало изучено и решение подобной задачи связано с большими трудностями.

В данном случае для трубопровода небольшой протяженности задача может быть упрощена и сведена к установившемуся движению изотермического ламинарного двухкомпонентного потока, в центре которого движется «холодная» часть (ядро потока), а в пристенном слое (кольцо толщиной δ) «горячая» часть. Оба компонента потока движутся соосно, т. е. симметрично относительно оси трубы. Расчетная схема представлена на рис. 2.12.

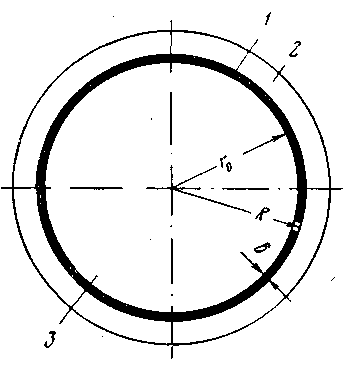
Рис. 2.12. К расчету нефтепровода с внешним обогревом.

1 — пристенный разогретый слой нефтепродукта; 2 — внешний обогрев; 3 — «холодное» ядро нефтепродукта в трубе.

При указанных упрощающих положениях дифференциальные уравнения движения примут вид:

для «холодного» потока

(2.52)

для «горячего» потока

(2.53)

где w — скорость потока; r — переменный радиус; μ— динамическая вязкость;

R — радиус трубы; — пьезометрический уклон.

В результате интегрирования уравнений (2.52) и (2.53) получим уравнения скоростей потоков:

Здесь с₁, с₂ и с'₁ с'₂ — постоянные интегрирования, определяемые из следующих граничных условий:

1) при r = R скорость потока горячей нефти (у стенки) равна нулю, т. е. w_г = 0

2) при r = r₀ (где r₀ — радиус границы раздела) скорости на границе раздела равны, т. е. w_x = w_г

3) при r = r₀ касательные напряжения «холодного» и «горячего» потоков равны, т. е. τ_х = τ_г

Дифференцируя уравнения скоростей, получаем

4) при r = 0 касательные напряжения на оси «холодного» потока равны нулю, т. е. τ_х = 0

Выполнение последнего условия возможно при с₁ = 0.

Тогда из третьего условия следует, что и с'₁ = 0, а согласно первому условию

Подставив значение с'₂ в равенство по второму условию, получим

Вносим значения постоянных с₁; с₂; с'₁ и с'₂ в уравнения скоростей:

Расходы «холодного» и «горячего» потоков получим, проинтегрировав уравнения скоростей:

т. е.

Общий расход трубопровода

или

(2.54)

Уравнение (2.54) можно упростить, если принять, что ρ_г≈ρ_х = ρ и μ=ρν, а также заменить =

Тогда, переходя к диаметру трубы, получим

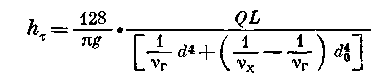(2.55)

Формула (2.55) позволяет определять потери напора на трение в трубопроводах с внешним обогревом при ламинарном режиме.

Кроме того, при отсутствии внешнего обогрева (ν_x = ν_r = ν) формула (2.55) обращается в известное уравнение Пуазейля:

При больших значениях ν_x величиной l/ν_x (по сравнению с l/ν_г) можно пренебречь. Тогда выражение в квадратных скобках (обозначим его буквой А) упростится:

Пренебрегая величинами δ², δ³ и δ⁴, как весьма малыми, получаем

Если подставить значение А в (2.55), получим уравнение для приближенных расчетов:

(2.56)

Из сравнения (2.56) и формулы Пуазейля видно, что чем больше вязкость основного (холодного) потока, тем выше эффективность внешнего обогрева:

(2.57)

Поскольку для коротких трубопроводов δ=const, величина k_э будет возрастать с увеличением вязкости холодного нефтепродукта.

Значение δ для практических расчетов отводных труб с внешним обогревом следует принимать в пределах от 0,5 до 1 мм.