§ 3. Гидравлический расчет трубопроводных коммуникаций слива нефтепродуктов из железнодорожных цистерн

Гидравлическим расчетам сливных коммуникаций должны предшествовать следующие работы:

1. выбор и обоснование способа слива;

2. разработка технологической схемы;

3. расстановка технологической арматуры;

4. определение основных высотных отметок;

5. определение длин (геометрической, эквивалентной, приведенной);

6. определение расчетного расхода, вязкости, скорости, рабочего давления. Различные системы нижнего слива можно разделить на две группы:

1. открытый слив (см. системы на рис. 1.12, а, б);

2. герметизированный слив (см. системы на рис. 1.12, в, г). Системы открытого слива могут работать и без «нулевого» резервуара. Рассмотрим в отдельности каждый из элементов системы нижнего слива.

Открытый слив Расчет сливных лотков и межрельсовых коллекторов

Сливные лотки и межрельсовые коллекторы представляют собой трубопроводы прямоугольного сечения, в которых происходит безнапорное движение жидкости, т. е. со свободной поверхностью. Для облегчения вывода формулы расчета пропускной способности таких трубопроводов введем следующие упрощающие положения:

1. движение установившееся, равномерное;

2. режим ламинарный;

3. сопротивление боковых стенок не учитывается.

При изложенных упрощающих положениях исходное дифференциальное уравнение запишется в виде.

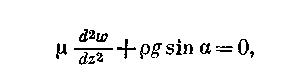(2.41)

где μ — динамическая вязкость в Па·с; w — скорость потока в канале в м/с; ρ — плотность нефтепродукта в кг/м³; g — ускорение силы тяжести в м/с²; α — угол наклона канала.

Расчетная схема представлена на рис.2.9.

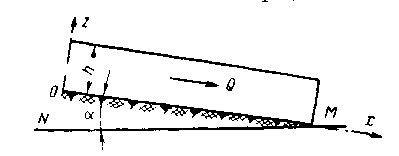
Рис. 2.9. К расчету безнапорных сливных коллекторов прямоугольного сечения.

Интегрируя уравнение (2.41), получаем

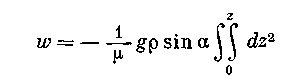
или (2.42)

Значение постоянных интегрирования с₁ и с₂ найдем из граничных условий: 1)при z = 0; w = 0 из уравнения (2.42)

2)при z = h касательные напряжения на поверхности потока = 0.

Согласно закона Ньютона

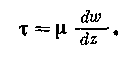
Дифференцируя уравнение (2.42), получаем

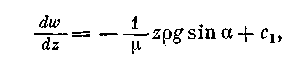
так как при z = h имеем = 0.

Отсюда

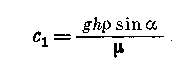
Подставив значения с₁ и с₂ в (2.42), получим уравнение скорости вязкой жидкости в прямоугольном канале при установившемся ламинарном режиме

Отсюда расход в канале «шириной» b будет:

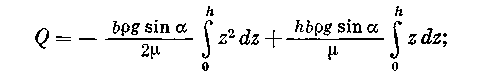
или, заменив μ=ρν

Известно, что для малых углов sin sin α ≈ tg α = i представляет уклон канала. В этом случае

или, обозначив =п,

(2.43)

Полное решение задачи о движении вязкой жидкости в прямоугольных каналах с учетом сопротивления у боковых стенок выполнено автором совместно с А. Ш. Асатуряном. Решение получено в виде гиперболических тангенсов и имеет вид

Исследование представленного ряда показывает его быструю сходимость, так как гиперболический тангенс изменяется от 0 до 1, а множитель = 0,027. Поэтому для практических расчетов можно ограничиться двумя членами ряда:

(2.44)

Оптимальное соотношение между высотой и шириной канала п_оп можно определить, исходя из условий наименьшего гидравлического сопротивления. Согласно формуле (2.23) для прямоугольных каналов потеря напора на трение при ламинарном режиме

где r— гидравлический радиус, т. е. отношение площади сечения потока (S) к его смоченному периметру (b+ 2h).

Из этой формулы следует, что наименьшие гидравлические сопротивления при заданной площади сечения потока соответствуют r_max. Максимальное значение r можно определить из условия = 0.

Полученный результат показывает, что из всех сечений наиболее близко приближается к полукругу, который имеет максимальный гидравлический радиус, прямоугольник с отношением сторон 1 : 2.

Поперечное сечение коллектора при турбулентном режиме можно определить по гидравлическому радиусу, пользуясь формулой (2.23):

(2.45)

где L — длина коллектора; Δz — разность отметок начального и конечного сечений коллектора.

Чтобы коллектор не лимитировал производительность слива, что возможно при поступлении в коллектор высоковязких и парафинистых нефтей и нефтепродуктов, необходимо подогревать дно коллектора. Помимо увеличения расхода подогрев дна коллектора позволяет легко удалять возможные осадки, особенно выпадающие в больших количествах из высокопарафинистых нефтей.

Расход в коллекторе прямоугольного сечения с обогревом дна (Q'_г) определяется по уравнению

(2.46)

где v_x и v_г — кинематическая вязкость основной массы холодного нефтепродукта и пристенного горячего слоя, соприкасающегося с обогреваемым дном, в м²/с; t_т — температура теплоносителя в °С; t_x и t_г — температуры холодного и горячего пристенного слоев нефтепродукта в °С; k— полный коэффициент теплопередачи от теплоносителя к нефтепродукту в Вт/(м² °С); L — длина коллектора в м; с — весовая теплоемкость нефтепродукта в Дж/(кг °С); ρ — плотность нефтепродукта в кг/м³.

При обогреве помимо дна и боковых стенок коллектора расход нефтепродуктов в таком безнапорном трубопроводе может быть определен из уравнения

(2.47)

Сравнивая уравнения (2.44), (2.46) и (2.47), можно определить, на сколько увеличится расход нефтепродуктов в обогреваемых коллекторах по сравнению с холодными: